题面
大秦 为你打开 题目传送门
看不了的就看下面罢
从一个 $n\times n$ 的矩阵中选出一个元素之和最大的非空子矩阵。
思路
思考一下,我们发现学过和这个最最有关的知识点应该是 “最大子段和” 。那么对于这道题的最大子矩阵应该怎么办呢?我们可以先参考一下最大子段和的代码。其主要思想就是能选就选,选不了就重开。
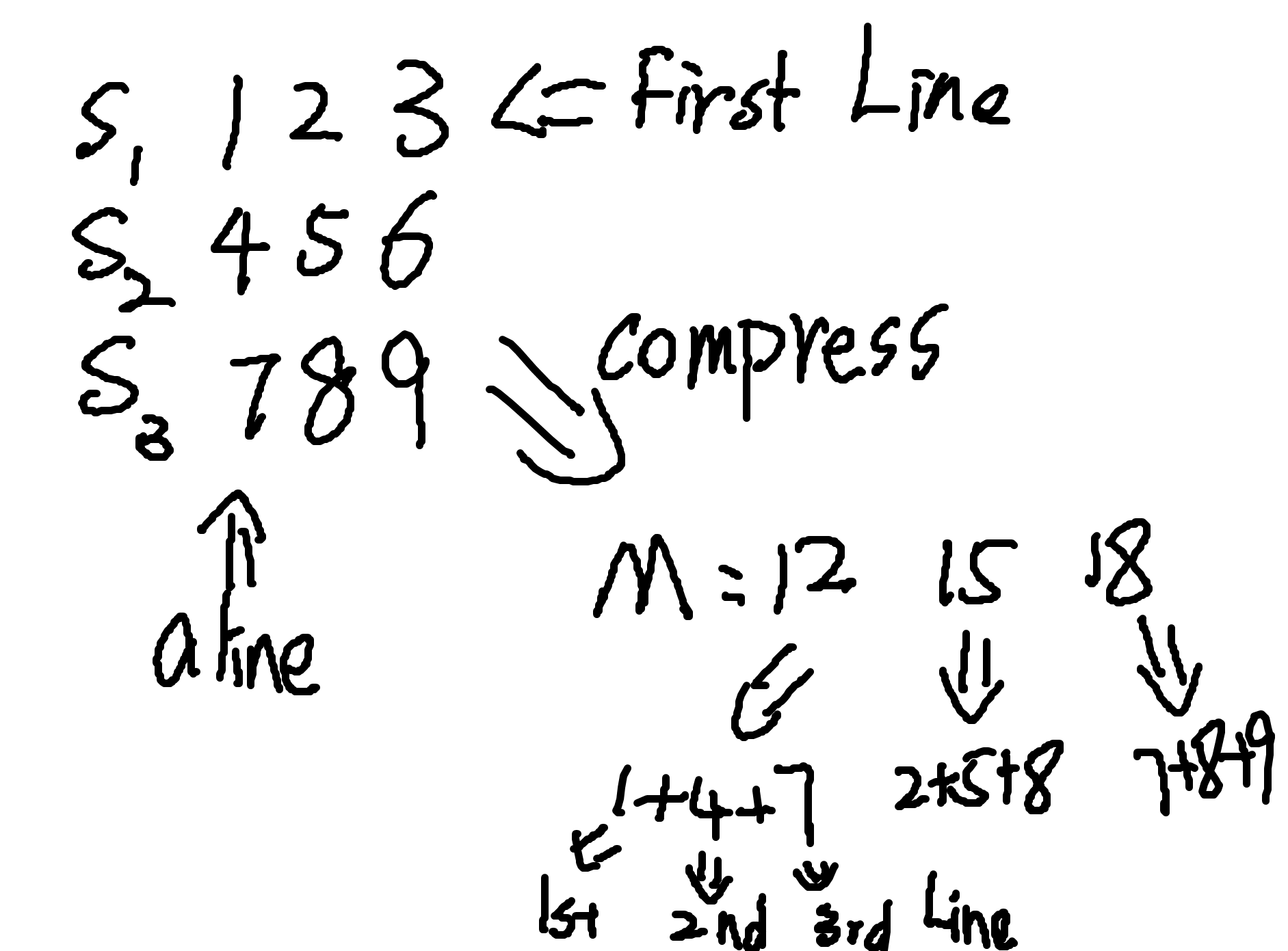
那么现在的问题是是否可以把最大子段和的思路借鉴到最大子矩阵中。矩阵本质上是一堆子段叠在一起得出的,且这些子段长度相等,一一对齐,才构造出了矩阵。我们将矩阵从上往下数的第一个子段称为第一行,那么一下所有字段的位置都是确定的了。那么我们就可以更具这个性质压缩一个矩阵。详见下图:

按照这个方法,我们把这个矩阵的第一行确定(假设是 $i$ )后,假设当前矩阵是 $k$ 行,那么就把给出的矩阵中的第 $i$ 至 $i + k -1 $ 行拿出来压缩。然后对于压缩出来的东西求最大子段和就可以了
我们设 $dp[i]$ 表示宽度(每一行的长度)为 $i$ 的最大子矩阵,答案就从所有里面最大的找。详见代码。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include<bits/stdc++.h>
using namespace std;
int n;
int a[110][110];
int s[110][110];
int dp[110];
void Input() {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
s[i][j] = s[i-1][j] + a[i][j];
}
}
}
void Work() {
int ans = -1280000;
for(int i = 1; i <= n; i++) {
for(int j = i; j <= n; j++) {
dp[0] = 0;
for(int k = 1; k <= n; k++) {
dp[k] = s[j][k] - s[i - 1][k];
if(dp[k - 1] > 0) dp[k] += dp[k - 1];
ans = max(ans, dp[k]);
}
}
}
printf("%d\n", ans);
}
int main() {
while(~scanf("%d", &n)) {
Input();
Work();
}
return 0;
}
|