算法简介:悬星尽散击云碎
一般来讲,我们在大值域的权值线段树问题的时候,都会考虑把它变成离线的,然后进行线段树操作。但是,以万恶的出题人视角,一定会把这唯一的路给断掉,也就是强制在线的大值域权值线段树问题,那么我们就要考虑到动态开点权值线段树了。至于动态开点线段树的应用……想必都知道了吧 —— 线段树合并。
算法演示:璇玑合璧镇昆仑
第一部分:星罗宿列天权临
那么既然要讲的是动态开点权值线段树的应用,自然要讲动态开点权值线段树。那么我们首先来想,动态开点权值线段树的内存理论应该是多少。首先我们想权值线段树的内存,就和普通线段树一样,都是开了 $4N$ 的,那么如果是动态开点,显而易见我们就可以达到线段树的理论内存,$N\log V$ 其中,$N$ 是数据范围,$V$ 是值域。
有人可能想不通:我们都不知道数据里面最大的那个数,怎么开始数组,怎么建树,怎么往下递归寻找答案?
上面这个有人是谁,我也不知道,但是有没有一种可能,我们是动态开点,我们不需要建树,我们的内存就是 $N\log V$ ,内存直接开到这么大就够了,也就是一般来讲的 N<<5 。这个 $5$ 的出处是 $2^{32} ≈ 2\times10^9$ 就是一般大小的值域。
OK,那么内存的问题解决以后,如何进行下一步呢?上面提到了,不需要建树,这是因为动态开点的意思就是有点就用没点就开,如果走到了一个不存在的点,新开一个就是,这也是为什么说不用建树,建树的过程其实就是一遍又一遍的插入操作中完成的。
那么如何进行插入操作呢?我们首先定义一个结构体,表示这一颗树的节点。
1
2
3
4
5
| struct Node {
int l, r;
int ans, sum ... ;
}node[N << 5];
int cntn = 1;
|
那么插入操作的内容就可以表示为和静态线段树差不多的形式:
1
2
3
4
5
6
7
8
9
10
| inline void Modify(int &p, int L, int R, int x, int v) {
if(!p) p = ++cntn;
if(L == R) {
}
int mid = L + R >> 1;
if(x <= mid) Modify(node[p].l, L, mid, x, v);
else Modify(node[p].r, mid + 1, R, x, v);
node[p] = node[node[p].l] + node[node[p].r];
}
|
这里插入的时候节点编号用了 & 目的是修改的时候能直接带着原来的值一起改掉,很方便。既然修改已经起了个头,那么其实查询也简单了。
1
2
3
4
5
6
7
8
| inline int Query(int p, int L, int R, int l, int r) {
if(!p) return 0;
if(L <= node[p].l && node[p].r <= R) return node[p].ans;
int ans = 0, mid = L + R >> 1;
if(l <= mid) ans += Query(node[p].l, L, mid, l, r);
if(mid < r) ans += Query(node[p].r, mid + 1, R, l, r);
return ans;
}
|
大概是这样。这就是动态开点权值线段树的全部内容了,修改和查询的时候 L,R 两个参数是值域的上下界。包括普通线段树的动态开点,都是可以这样写出来的。
第二部分:攻守易形著神机
那么接下来的重要部分,就是线段树合并。所谓线段树合并,字面意思的来讲,就是线段树的合并。显而易见这个算法的实现用静态数组绝对爆炸,所以说,我们就要引入上个部分的动态开点线段树。那么动态开点线段树,为什么更加容易进行合并呢。一是内存问题,动态的开点,内存绝对比静态好很多,因为静态就是真正意义上的静态,空间浪费很严重,但是动态开点,内存取决于插入操作的数量,这就是为什么说动态开点可以用于处理这样的问题。
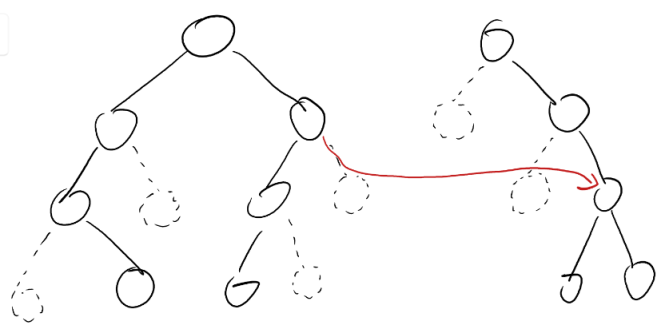
那么想要用动态开点实现线段树合并,显而易见有两个部分,共同存在的点和非共同存在的点。如果是共同存在的点,好说,直接把他们处理的答案处理一下,但是不是共同存在的点,就不一样了,我们要考虑是在被合并的点的基础上,进行新建操作呢,还是直接把儿子的指针指向他们。显而易见的选后者,一来这样复杂度较小,二来就是线段树合并的核心部分,这个后面会提到,暂且卖个关子。图示的话,大概是下面这样:

其他的点要么是保留,要么是合并。这样是线段树合并的思想,但是,这样的复杂度是多少呢?我们可以大概的算一算,首先,对于所有线段树的总结点数,一定是 $N\log N$ 的。那么我们如何去推算线段树合并的总结复杂度呢?
每次合并,显然重复的点会被叠加掉,然后就不会有他们的存在了。也就是说每次合并一定至少减少一个点,总复杂度就是 $N\log N$ 了。
有了思路,代码也绝对不难写,大概就是下面这样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| int merge(int a,int b,int l,int r)
{
if(!a) return b;
if(!b) return a;
if(l==r)
{
return a;
}
int mid=(l+r)>>1;
tr[a].l=merge(tr[a].l,tr[b].l,l,mid);
tr[a].r=merge(tr[a].r,tr[b].r,mid+1,r);
push_up(a);
return a;
}
|
这个就是线段树合并的大致思路了。
第三部分:琼屏千扇正天衡
常规来讲,接下来就是例题部分了,这里给讲一道之前用启发式合并做的题目,CF600E。
那么这道题如何用线段树合并做呢,直接大力对于每个子树建立线段树,一直往根合并,处理答案即可。
代码的话,摘自 线段树合并:从入门到放弃 - 洛谷专栏 ,也是个不错的文章~
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
| #include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lson tr[now].l
#define rson tr[now].r
#define int long long
using namespace std;
struct tree
{
int l,r,sum,val,ans;
}tr[5000050];
int rt[100010],cl[100010],cnt,n,anss[100010];
vector<int> g[100010];
int push_up(int now)
{
if(tr[lson].sum>tr[rson].sum)
{
tr[now].sum=tr[lson].sum;
tr[now].val=tr[lson].val;
tr[now].ans=tr[lson].ans;
}
if(tr[rson].sum>tr[lson].sum)
{
tr[now].sum=tr[rson].sum;
tr[now].val=tr[rson].val;
tr[now].ans=tr[rson].ans;
}
if(tr[lson].sum==tr[rson].sum)
{
tr[now].sum=tr[lson].sum;
tr[now].val=tr[lson].val;
tr[now].ans=tr[lson].ans+tr[rson].ans;
}
}
int update(int &now,int l,int r,int pos,int v)
{
if(!now) now=++cnt;
if(l==r)
{
tr[now].val=l;
tr[now].sum+=v;
tr[now].ans=l;
return 0;
}
int mid=(l+r)>>1;
if(pos<=mid) update(lson,l,mid,pos,v);
else update(rson,mid+1,r,pos,v);
push_up(now);
}
int merge(int a,int b,int l,int r)
{
if(!a) return b;
if(!b) return a;
if(l==r)
{
tr[a].val=l;
tr[a].sum+=tr[b].sum;
tr[a].ans=l;
return a;
}
int mid=(l+r)>>1;
tr[a].l=merge(tr[a].l,tr[b].l,l,mid);
tr[a].r=merge(tr[a].r,tr[b].r,mid+1,r);
push_up(a);
return a;
}
int dfs(int now,int f)
{
for(int i=0;i<g[now].size();i++)
{
if(g[now][i]==f) continue;
dfs(g[now][i],now);
merge(rt[now],rt[g[now][i]],1,100000);
}
update(rt[now],1,100000,cl[now],1);
anss[now]=tr[rt[now]].ans;
}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&cl[i]);
rt[i]=i;
cnt++;
}
int from,to;
for(int i=1;i<n;i++)
{
scanf("%lld%lld",&from,&to);
g[from].push_back(to);
g[to].push_back(from);
}
dfs(1,0);
for(int i=1;i<=n;i++)
{
printf("%lld ",anss[i]);
}
}
|
算法实战:七星璨璨凝流光
查看相关算法标签喵!