Math Combinatorial Counting [I]

Definition of Combinatorial Counting

We all have studied some basic Combinatorial Counting in primary , middle or high school. But now I still want to tell you the definition of Combinatorial Counting.

The Combinatorial Counting is a old things in math. Know we will get many branch in math that have some correlation with Combinatorial Counting.

I think the Combinatorial Counting is a way to discuss the method to calculate a combo of set. We all know we have such as problem in primary :

Problem :

We have a string and the length of it is 4 . For every $i\ (1\le i \le 4)$ , the $i$-$\tt th$ character in string is a little case letter from a to z .

The Answer of this problem is self-evident. Each character have $26$ choice and we have four character. So we can accord to Multiplication get the answer is $26^4$ .

In this example, we found basically kind of Combinatorial Counting : Multiplication , also the Addition principle .

Basic Form of Combinatorial Counting

We have a lot of ways to Mapping some information. Like the example we provided, you can think that it is a mapping from the index of string and the little case letter. The common Mapping have three types : injection, surjective and bijection. I will introduce them one by one after I tell you some basic concepts.

Basic Concepts

I have already said, I think the Combinatorial Counting is the number of methods for combining sets. Set is a easy concepts in high-school.

Definition

In mathematics, a set is defined as a collection of distinct, well-defined objects forming a group. There can be any number of items, be it a collection of whole numbers, months of a year, types of birds, and so on. Each item in the set is known as an element of the set. We use curly brackets while writing a set.

E.G.

We can consider a example of set : $A = \{0,1,2,3,4\}$

But, what is the “well-defined” means? We can make a set and the element in it can be : all the odd from $1$ to $n$ , all the number can divisible by 3, $\tt etc$. But we cannot make a set with the brave student in our class, ‘Brave’ is not a definite standard, so set cannot have such as elements. This is the “well-defined” means that we mentioned.

Symbol

More common symbol we all have studied in High-school, like $\in\ \notin\ \subset \ \subseteq\ \dots$ But now, we have a new symbol to represent the size of the set :

• For a set $A$ , we can use $|A|$ to represent the size of the set.
• We also can use #$A$ to represent the size of the set, it have same meaning with $|A|$ .

In order to made our writing more convenient, we have a simple symbol to represent a special type of set :

• $[n]$ this symbol means we have a set and the elements in it is from $1$ to $n$ . You also can write it by $\{a | a \in \operatorname N^\ast , a\le n\}$ , it is the descriptive approach we have studied in High-school.

E.G.

$\Big|[n]\Big| = n$

Mapping

Mapping is a way to map something to something, you can consider it is a function from a set to another set. We have a basic proposition for Mapping :

Prop. 1

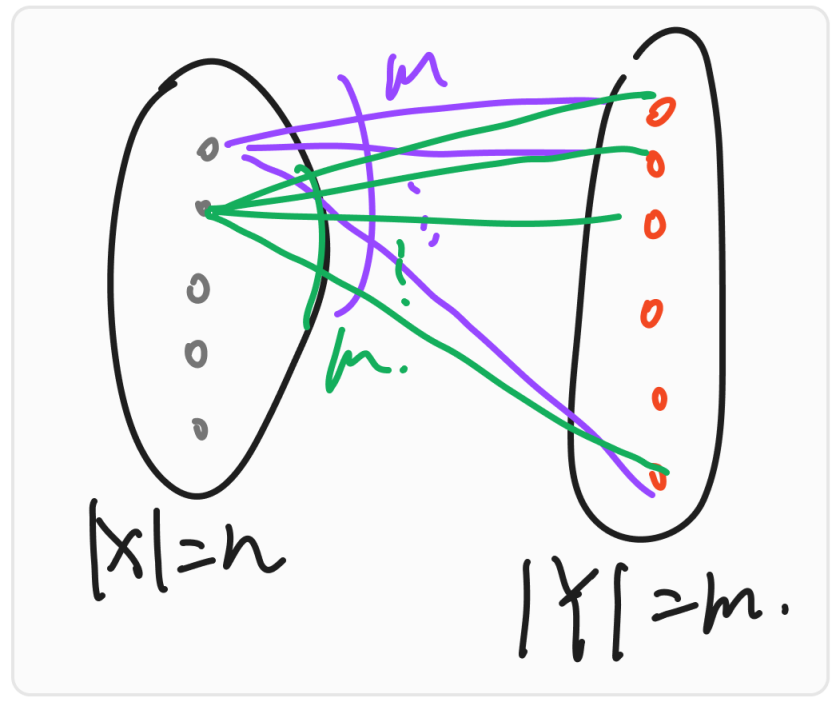
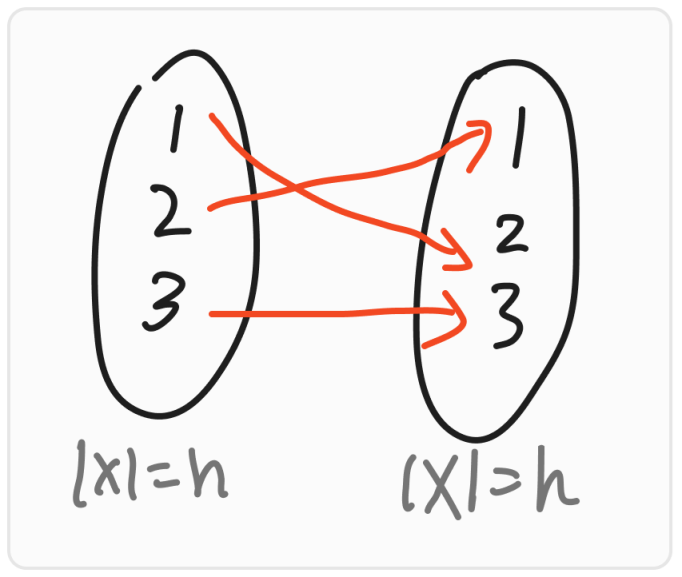
Let $X,Y$ be two set with $|X| = n, |Y| = m$ , the total number to mapping set $X$ to $Y$ ( different elements in $X$ can map same elements in $Y$ , yes, it is a basic Mapping ) $\operatorname F(X) \rightarrow Y$ is $|Y|^{|X|} = m^n$ .

Proof. 1

But why? We can prove this proposition in Combinatorial Counting.

We can draw a picture like below :

It is the Multiplication we mentioned, Every elements in $X$ can map all the element in $Y$ , we have $|X| = n$ and $|Y|=m$ , so the answer is $\underbrace{m\times m \times \cdots \times m}_n = m^n$ .

Mapping have three special type, Injection, Surjection and Bijection.

Injection

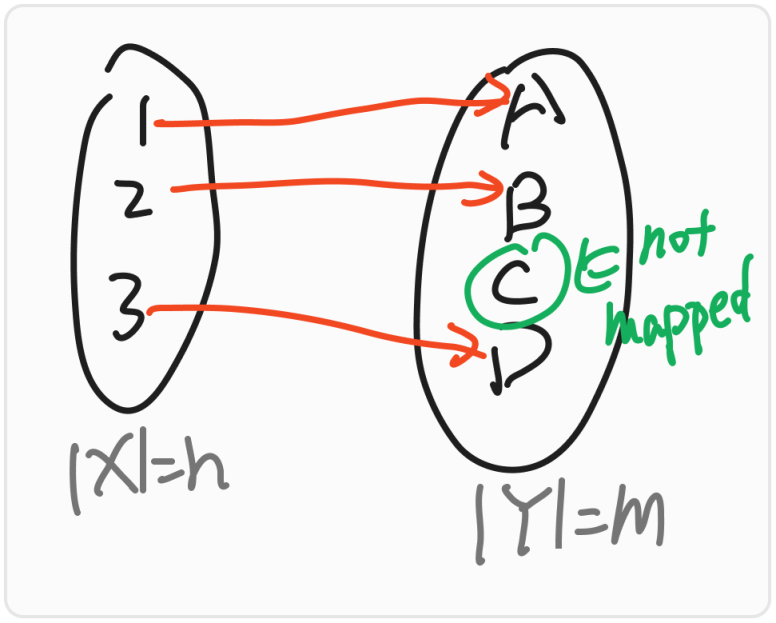
We can change a little point in the Basic Mapping , We know in the Basic Mapping different elements can map same element, it is not available in some time, so we change this things to “different elements must map different elements” it will turn to a Injection.

Prop. 2

Assume $|X| \le |Y| \ \ (|X| = n, |Y| = m)$ , the number of Injective Mappings $\operatorname F(X)\rightarrow Y$ is $(m)_n$ .

Proof. 2

Because we cannot choose same elements with different elements, If the first element in $X$ choose a element in $Y$ , the second element in $X$ cannot choose it. So the choice will getting less and less. We can get the answer is $m \times (m - 1) \times (m - 2) \times \cdots \times (m - n + 1)$ , but the proposition we said is $(m)_n$ , why?
tips : $(x)_y$ is a new symbol means that we combo multiple from $x$ to $x - y + 1$ , just know this is enough.

Warning! : Injection just let $|X|\ge |Y|$ to make sure all the element in $X$ can map a element in $Y$. It means that elements in $Y$ can not be mapped completely.

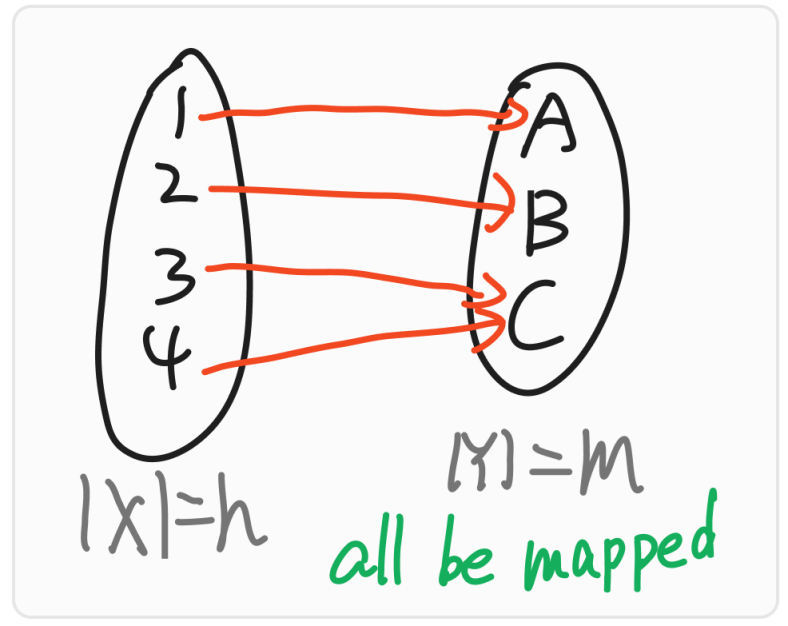
Surjection

Don’t like Injection, Surjection is the enhanced version of Injection. Injection define the set $X$ must all be mapped, but Surjection must let set $X$ and $Y$ all be mapped, it means element in $X$ must have a mapped value, and all the value mapped by element in $X$ can make a set and it is equal to set $Y$ . We can draw the picture below.

It is a difficult situation for now, It will be more easy after we studied Combination number. So just wait, we will learn it later.

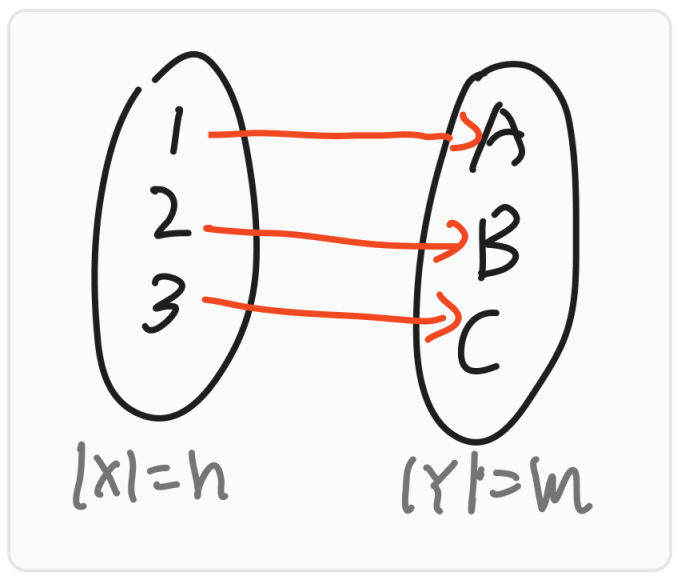
Bijection

Bijection is the sum of Injection and Surjection. It means, all the element in set $X$ can mapped a element in set $Y$ and all of them can full mapped and no same mapped value with different element. So the Bijective mappings Function can represent by the below picture.

Now we can going to next part of Combinatorial Counting!

Power Set

Power Set is a new calculate of set. First we can discuss all the subset of set $X$ to introduce it.

Prop. 3

The number of all the subset of $X$ is $2^{|X|}$ .

Proof. 3.1

We can discuss all the element in $X$ choose or not choose. So all the element in $X$ have 2 choices, we can get the answer $2^{|X|}$ from Multiplication.

Proof. 3.2

We can prove it from mapping. We can define a Basic Mapping Function : $\operatorname F(X) \rightarrow \{0,1\}$. If a element mapped value $1$ so it will be chosen in set $A$ . All the chosen element can be a subset of $X$ , So the number of Mappings we can calculate from Prop. 1. We can get a function below :

$$\forall A \subseteq X, \operatorname{F}(x\in X) = \begin{cases} 0,&x\notin A\\ 1,&x\in A \end{cases}$$

We define all the element in set $X$ have $k$ choices use power set to represent, write like $k^X$. Like the Prop. 3. we can use $2^X$ to represent the set composed by all the subset of set $X$.

E.G.

$2^X = \{A | A \subseteq X\}$
$|2^X| = 2^{|X|}$

Permutation

Permutation we know it is a unique array of origin array and all the element in array is mapped one by one. Think about it, maybe it is similar with Bijection? Yes, you are right. We can define a function $\operatorname F(X)\rightarrow X$ (Because of the disorder of set)

We can write it like below:

$$\dbinom{1 \quad 2\quad 3}{2\quad 1\quad 3}$$

The upper array is origin set, the lower array is the mapped value of element in $X$. Because Bijection is a special type of Injection, We can use Prop. 2 to calculate the number of different permutation of n-element set. The answer is $(|x|)_{|x|}$ , we can use a new symbol to represent it. It called factorial, write by $n! = (n)_n$ . Specially, $0!=1$ .

Prop. 4

$(n)_n=n!\ ,\ 0!=1$

Combinatorial Number

In fact, Combinatorial Number we have get a little point in the pre part of this article, so what is it? we can start it from a little story …

Binomial coefficient

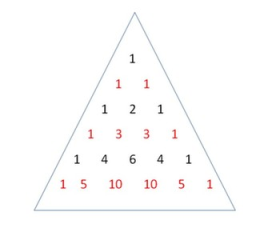
Binomial coefficient is a fantastic coefficient of binomial, long long years ago in Accident China, there is a people named $\tt Yang\ Hui$ found a special triangle, now we called it Pascal’s triangle. The element in Triangle have such as special point :

1. If a element is at side or top , it must be $1$ .
2. Other element in triangle is the sum of two element on it.

If we use a number $C_{n,k}$ to represent the element in Triangle on row $n$ and it is $k + 1$ -$\tt th$ element, we can get such as function :

$$C_{n,k} = \begin{cases} 1,& k=0\ or\ k=n\\ C_{n-1,k-1} + C_{n-1,k} & \operatorname{other.} \end{cases}$$

This special number $C$ is the Combinatorial Number or Binomial coefficient we said, we also use $\dbinom{n}{k}$ to show it.

Formula

We know what is Binomial coefficient, but how to calculate it? we have such as Formula.

$$\dbinom{n}{k}=\cfrac{(n)_k}{k!} = \cfrac{n!}{k!(n-k)!}$$

So, why? Consider a Injective Mapping $\operatorname F([k]) \rightarrow X$ , $X$ is a n-element set. The element in $X$ who be mapped by element from $1$ to $k$ in $[k]$ is a Binomial coefficient of it. But Injection have different mapped value like $\operatorname F(1) \rightarrow A$ and $\operatorname F(2) \rightarrow B$ is not equal to $\operatorname F(2) \rightarrow A$ and $\operatorname F(1) \rightarrow B$ . But for Binomial coefficient, it is same because set is disorder. The number of permutation of a k-element set is $k\ !$ so we get the formula.

Prop. 5

For a set $X$ with size $n$ , Let $\dbinom{X}{k}=\{A | A\subseteq X, |A|=k\}$ , $\left|\dbinom{X}{K}\right| = \dbinom{|X|}{K}$ .

Proof. 5

Easy to prove. If you cannot prove it, go back read again.

Special Equation

• $\dbinom{n}{k}=\dbinom{n}{n-k}$

  Proof. 1.1

  Prove it on the definition. we all know

  $\dbinom{n}{k} = \cfrac{n!}{k!(n-k)!}$

  if we change $k$ to $n-k$ , it will be same :

  $\dbinom{n}{n-k} = \cfrac{n!}{(n-k)!k!}$

  QED.

  Proof. 1.2

  Prove it in Combinatorial. Think about it : we choose $k$ element in $n$ element is the definition of $\binom{n}{k}$ , but choose $n-k$ element in $n$ elements we can understand that not choose $k$ element in $n$ elements, it is same.

• $\sum\limits_{i=0}^n \dbinom{n}{i} = 2^n$

  Proof. 2

  $\dbinom{n}{k}$ is the number of subset of size $k$ in all the subset of a n-element set. the sum of them is all the number of subset of a n-element set, use Prop. 3 can do it.

• $\dbinom{n}{k}=\dbinom{n-1}{k-1} + \dbinom{n-1}{k}$

  Proof. 3

  Pascal’s Triangle.

The Binomial Theorem

For any integer $n\ge 1$ holds for any real $x$ , we have :

$$(x+1)^n=\sum\limits_{k=0}^n \dbinom{n}{k}x^k$$

Proof. 6.1

Each item must choose $x$ or $1$ , so use Combinatorial Number can know this Theorem.

Proof 6.2

Try to use Mathematical induction : Assume is hold for $n-1$

$$\begin{aligned} (x+1)^n &= (x+1)\times (x+1)^{n-1}\\ &= (x+1)\sum\limits_{k=0}^{n-1} \dbinom{n-1}{k} x^{k}\\ &= x\times\sum\limits_{i=0}^{n-1} \dbinom{n-1}{i} x^{i} + \sum\limits_{i=0}^{n-1} \dbinom{n-1}{i} x^{i} \end{aligned}$$

Then found the lowest item and highest item of it. If we get $i = 0$ , we will get lowest case $1$ . And we will get highest case of $i=n-1$ . Then the equation will be :

$$\begin{aligned} (x+1)^n &= x\times\sum\limits_{i=0}^{n-1} \dbinom{n-1}{i} x^{i} + \sum\limits_{i=0}^{n-1} \dbinom{n-1}{i} x^{i} \\ &= 1 + \sum\limits_{i=1}^{n-1}\left(\dbinom{n-1}{i} + \dbinom{n-1}{i-1}\right)x^i+x^n \end{aligned}$$

so the theorem is true.

Extension

We have Multinomial Coefficient :

$$\dbinom{n}{k_1\ k_2 \cdots \ k_m} = \cfrac{n!}{k_1!\ k_2! \cdots \ k_m!}$$

we have Multinomial Theorem :

$$(x_1+ x_2 + \cdots + x_m)^n=\sum\limits_{\forall k_i\ge 0}^{k_1+k_2 + \cdots+k_m=n} \dbinom{n}{k_1\ k_2 \cdots \ k_m}{x_1}^{k_1}{x_2}^{k_2}\cdots{x_m}^{k_m}$$

---

Example Problem

Problem 1 :

How many subsets of odd size are there in $[n]$ ?

Problem 2 :

Fixed $n \ge m$ , please prove $\sum\limits_{k=0}^n \dbinom{n}{k} \dbinom{k}{m} = \dbinom{n}{m}2^{n-m}$

Problem 3 :

How many solutions $(x_1, x_2,\dots, x_n)$ to the equation : $x_1 + x_2 + \cdots + x_n = k\quad \forall x_i\in\{0,1\}$

Problem 4 :

Assume $k\ge n$ , How many $(x_1, x_2, \dots , x_n)$ to the equation : $x_1 + x_2 + \cdots + x_n = k\quad \forall x_i\ge1$

Problem 5 :

Assume $k\ge n$ , How many $(x_1, x_2, \dots , x_n)$ to the equation : $x_1 + x_2 + \cdots + x_n = k\quad \forall x_i\ge0$

Problem 6 :

How many subset of odd size in $[n]$ ? (Use Binomial Theorem to prove.)

---