算法简介：赤沙的归嗣

莫队算法是由莫涛提出的算法。在莫涛提出莫队算法之前，莫队算法已经在 Codeforces 的高手圈里小范围流传，但是莫涛是第一个对莫队算法进行详细归纳总结的人。莫涛提出莫队算法时，只分析了普通莫队算法，但是经过 OIer 和 ACMer 的集体智慧改造，莫队有了多种扩展版本。莫队算法之所以叫做莫队算法，是因为莫涛是当时的国家队队长，至今莫队算法依然被称为 Mo's Algorithm 。

莫队算法可以解决一类离线区间询问问题，适用性极为广泛。同时将其加以扩展，便能轻松处理树上路径询问以及支持修改操作。

算法试用：贯月的耀锋

算法推导：织狩的奉祀

莫队算法是一种基于分块的算法。其原理在于对于所有的询问离线，而离线后我们对于每一个询问所在的左右端点的位置进行分块，首先对于左端点排序，如果不在同一个块，我们就可以比较左端点，如果在一起，我们就要看左端点所在块的奇偶性。如果块是奇数，r 按从小到大排序，如果块是偶数，r 从大到小排序，这样我们的 r 指针在处理完这个奇数块的问题后，将在返回的途中处理偶数块的问题，再向 n 移动处理下一个奇数块的问题，优化了 r 指针的移动次数，一般情况下，这种优化能让程序快很多很多。（我曾在洛谷 P1972 用此方法把 40pts 改到了 50pts ）

然后我们暴力的去找到当前的询问区间，这里就需要莫队的必要条件：操作可 O(1) 在边界拓展 1 。由此性质，代码也不会繁杂。

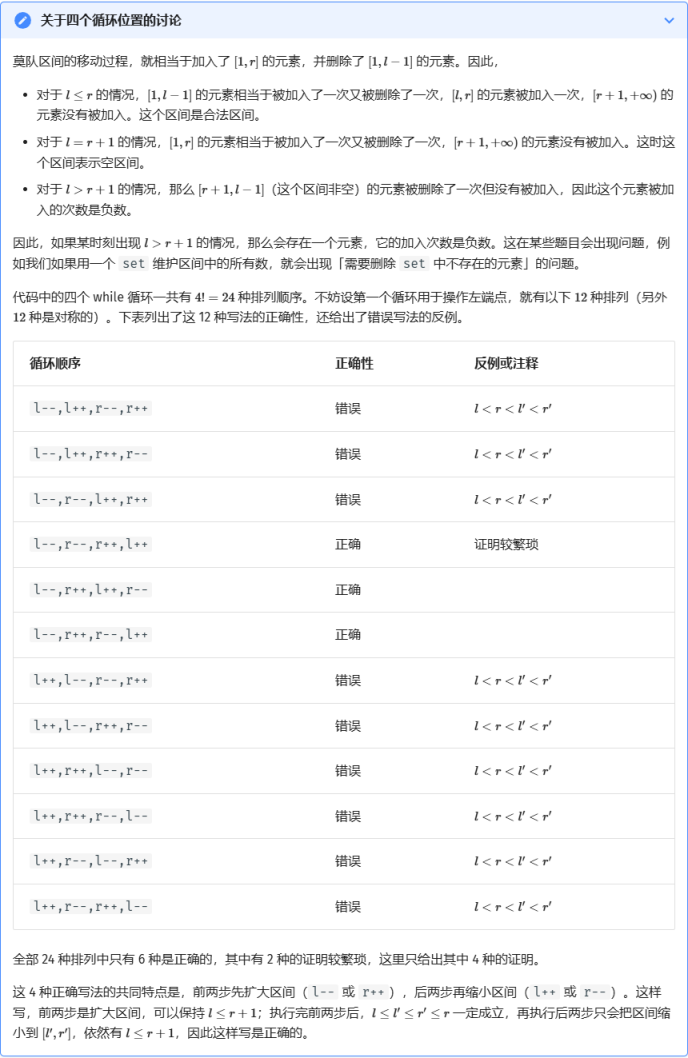
但是值得注意的是，莫队算法经行拓展的时候左右端点的移动方式会直接影响正确性，详见 $\tt OI\ Wiki$

算法演示：守戍的誓命

这个是我的 P1972 的莫队代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
// #pragma GCC optimize(2)
// #pragma GCC optimize(3, "Ofast", "inline")
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>

namespace FastIO 
{
    char buf[110], *p1, *p2;
    #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
};
using namespace FastIO;

const int N = 1e6 + 10;

int n, Q;
int a[N];

int B, cnt[N], ans;
int pos[N], res[N];

struct Qiz {
    int l, r, id;
    inline bool operator < (const Qiz &x) const {
        if(pos[l] != pos[x.l]) return l < x.l;
        return (pos[l] & 1) ? r < x.r : r > x.r;
    }
}qs[N];

inline void Input() {
    read(n);
    B = (int)pow(n, 0.5);
    for(int i = 1; i <= n; i++) {
        read(a[i]);
        pos[i] = i / B;
    }
    read(Q);
    for(int i = 1; i <= Q; i++) {
        read(qs[i].l, qs[i].r);
        qs[i].id = i;
    }
    return ;
}

inline void Upd(int x, int f) {
    x = a[x];
    cnt[x] += f;
    if(cnt[x] == 0 && f == -1) return (void)ans--;
    if(cnt[x] == 1 && f == 1) return (void)ans++;
    return ;
}

inline void Work() {
    std::sort(qs + 1, qs + Q + 1);
    for(int i = 1, l = 1, r = 0; i <= Q; i++) {
        const Qiz &q = qs[i];
        while (l > q.l) Upd(--l, +1);
        while (r < q.r) Upd(++r, +1);
        while (l < q.l) Upd(l++, -1);
        while (r > q.r) Upd(r--, -1);
        res[q.id] = ans;
    }
    for(int i = 1; i <= Q; i++) {
        printf("%d\n", res[i]);
    }
    return ;
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

算法实战：萦金的苍瞳

查看相关算法标签喵！