A - Lex String
Problem - A - Codeforces
题意
给定两个没有相同字符的字符串 $a,b$ 。每回合轮流从任意一个字符串中任意取一个字符,并插入到一个字符串 $c$ 的末尾。要求不能连续取同一个字符串中的字符大于 $k$ 次,如果两个字符串中有一个空了,
题解
模拟即可,注意题目中强调的细节即可。
B - Mystic Permutation
Problem - B - Codeforces
题意
给出一个排列 $[1,n]$ ,要求构造一个排列 $[1,n]$,使得这两个排列之间的任意一个相同位置的元素都不相同,且满足这个排列的字典序最小。 如果无法构造出这样的序列则输出 $-1$ 。
题解
正常贪心即正解,优先摆小的,如果相同就摆下一个,如果是最后一个就和前一个交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| inline void Work() {
if(n == 1) {
printf("-1\n");
while(!q.empty()) q.pop();
return ;
}
for(int i = 1; i <= n; i++) {
int tp = q.top(); q.pop();
if(tp == a[i]) {
if(q.empty()) {
b[i] = tp;
swap(b[i], b[i-1]);
}
else {
b[i] = q.top(); q.pop();
q.push(tp);
}
}
else {
b[i] = tp;
}
}
while(!q.empty()) q.pop();
for(int i = 1; i <= n; i++) {
if(b[i] == a[i]) {
printf("-1\n");
return ;
}
}
for(int i = 1; i <= n; i++) {
printf("%d ", b[i]);
}
printf("\n");
}
|
C - Infected Tree
Problem - C - Codeforces
题意
给定一棵以 $1$ 号节点为根的二叉树,总节点个数为 $n$ 。
现在 $1$ 号节点感染了病毒,病毒每一回合都会去感染与该节点直接相连的节点,而你在这一回合里可以选择删除任意一个没有被病毒感染(尚未被删除)的点,这样就断开了它与其直接相连的点得关系.
询问最多可以有多少不被病毒感染的点,被删除的点不算做不被病毒感染的点
题解
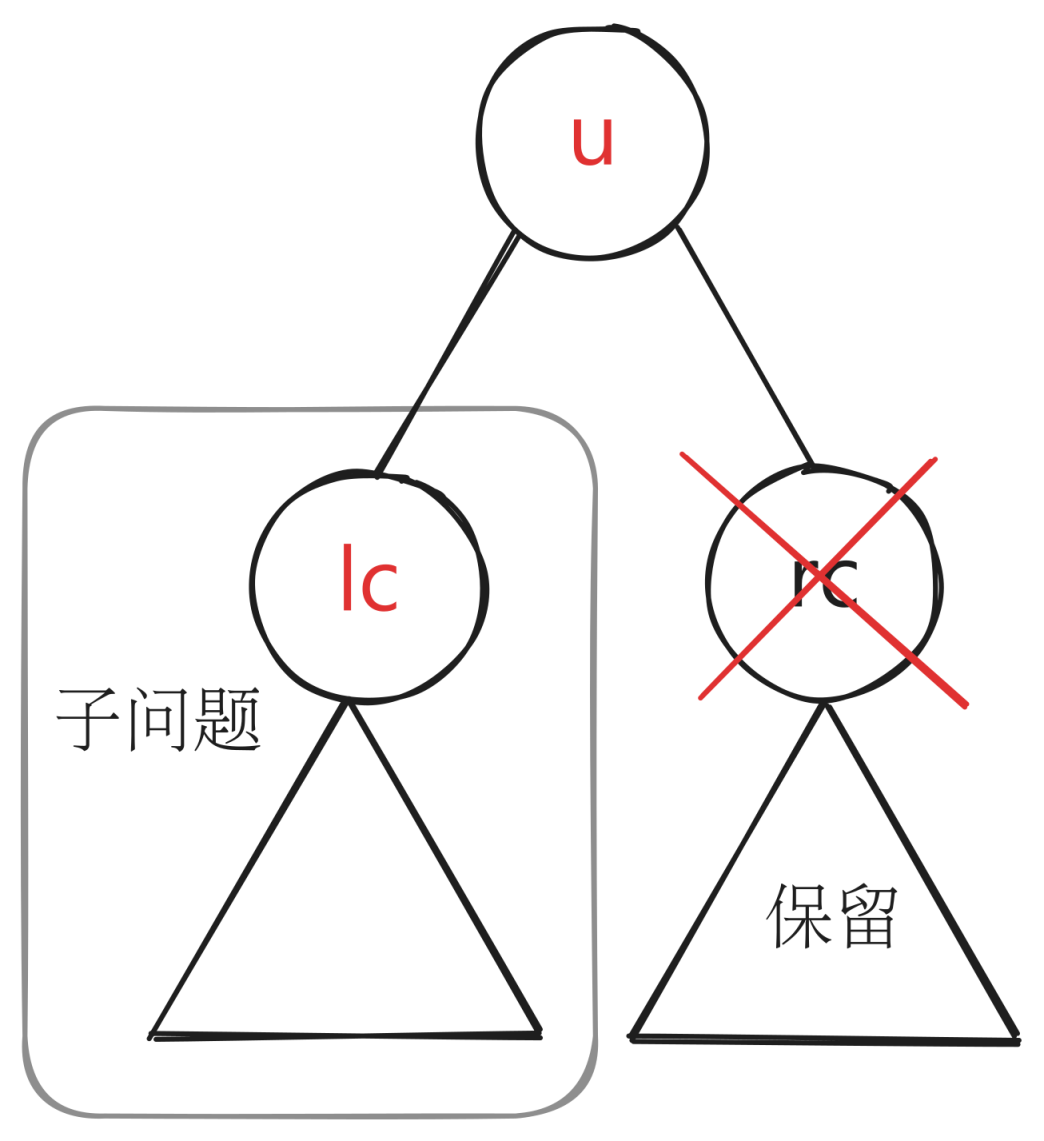
一眼树形DP。设置状态 $dp[u]$ 表示:以 $i$ 为根的子树中,若 $i$ 被感染了,最多能保留多少个节点。
考虑转移。注意到这是一颗二叉树,所以转移就很简单了:$dp[u]=\max(dp[lc]+sz[rc]-1,dp[rc]+sz[lc]-1)$ 。
实际意义如图所示:

D - Lena and Matrix
Problem - D - Codeforces
题意
给定一个由字符 W 或 B 组成的 $n\times m$ 的矩阵。求这样一个点的坐标,满足其到图中任何一个 B 的最大曼哈顿距离最小。
题解
首先尝试平均数和中位数,发现都不对,卡掉他也很简单,让大多数的点聚集在一个地方,然后放一个点在一个很远很远的地方,这样就能卡掉平均数和中位数。
接下来考虑正解。我们会发现题目让我们维护的答案核心其实是下边的那个式子:
众所周知,曼哈顿距离不容易维护的话我们还有另外一个常用的距离:切比雪夫距离。如果用切比雪夫距离表示的话,答案就显而易见了:
简单转化一下就可以得到:$\max(\max(|X-x_i|), \max(|Y-y_i|))$。
这个显然非常容易维护,直接把最后的答案得出后转换回曼哈顿即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include<bits/stdc++.h>
#define LL long long
using namespace std;
const LL N=2005;
LL T,n,m,a[N][N],ansx,ansy;
vector<LL>v1,v2;
char c;
LL cal(LL xx,LL yy)
{
return max({xx-v1[0],yy-v2[0],v1[v1.size()-1]-xx,v2[v2.size()-1]-yy});
}
int main()
{
cin>>T;
while(T--)
{
cin>>n>>m;
ansx=1e9;
v1.clear(),v2.clear();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>c;
if(c=='B')
{
v1.push_back(j-i);
v2.push_back(i+j);
}
}
}
sort(v1.begin(),v1.end());
sort(v2.begin(),v2.end());
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
LL xx=j-i,yy=i+j;
if(cal(xx,yy)<cal(ansy-ansx,ansy+ansx))
{
ansx=i,ansy=j;
}
}
}
cout<<ansx<<' '<<ansy<<endl;
}
}
|
E - ANDfinity
Problem - E - Codeforces
题意
从计算机科学系毕业后, Vlad 被奖与一个由 $n$ 个非负整数组成的数组 $a_1,a_2, \dots , a_n$。他很自然地想到构建一个有 $n$ 个点,编号为 $1,2,\dots,n$ 的图。点 $i$ 和 $j$ 之间有边当且仅当 $a_i\& a_j >0$,其中 $\&$ 表示按位与。
Vlad 希望这张图连通,虽然最初可能不是这样。为了使图连通,他可以对这个数组做下列两种操作:
- 选择一个元素 $a_i$ 并将它加一。
- 选择一个元素 $a_i$ 并将它减一(仅能在 $a_i>0$ 时做此操作)。
可以证明存在一个有穷的操作序列使得这张图连通。所以,你能帮 Vlad 找到最少的可能操作数以达成这个目标并给出操作方法吗?
题解
首先注意到 $0$ 一定要变为 $1$ 才可以联通,鱼逝先优先变 $0$ 。
接下来观察性质。
考虑贪心,对于 lowbit 最大的数,对其减一,如果不止一个,那么随机取一个加一即可。
证明很简单,因为 lowbit 最大的数减一以后,剩下的几位就都变成了一;如果还有的话就会连不上,我们加一就有一定能连上。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
|
#include<bits/stdc++.h>
#pragma GCC optimize("Ofast")
#pragma GCC optimize("unroll-loops")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native")
using namespace std;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
int a[2003],n,ans,x,s;
bool vis[2003];
int fa[2003];
void dfs(int x)
{
vis[x]=1,++s;
for(int i=1; i<=n; ++i)
if((a[i]&a[x])&&!vis[i])
dfs(i);
return ;
}
int L(int x){return x&(-x);}
int find(int x){return fa[x]==x?x:(fa[x]=find(fa[x]));}
bool chk()
{
for(int i=1; i<=n; ++i) fa[i]=i;
for(int s=1; s<=536870912; s<<=1)
{
int fir=n;
for(int i=1; fir==n&&i<n; ++i) if(a[i]&s) fir=i;
int A=find(fir);
for(int i=fir+1; i<=n; ++i) if(a[i]&s) fa[find(i)]=A;
}
for(int i=2; i<=n; ++i) if(find(i)!=find(1)) return 0;
return 1;
}
signed main()
{
for(int T=read();T--;)
{
n=read(),ans=x=s=0;
for(int i=1; i<=n; ++i) vis[i]=0;
for(int i=1; i<=n; ++i)
(!(a[i]=read()))&&(++ans,a[i]=1),
x=max(x,L(a[i]));
dfs(1);
if(s==n)
{
printf("%d\n",ans);
for(int i=1; i<=n; ++i) printf("%d ",a[i]);
puts("");
}
else
{
int ovo=1;
for(int i=1; i<=n; ++i)
{
--a[i];
if(chk()){ovo=0;break;}
++a[i],++a[i];
if(chk()){ovo=0;break;}
--a[i];
}
if(!ovo)
{
printf("%d\n",ans+1);
for(int i=1; i<=n; ++i) printf("%d ",a[i]);
puts("");
continue;
}
for(int i=1; i<=n; ++i)
if(L(a[i])==x)
{
if(ovo)
--a[i],ovo=0;
else
{
++a[i];
break;
}
}
printf("%d\n",ans+2);
for(int i=1; i<=n; ++i) printf("%d ",a[i]);
puts("");
}
}
return 0;
}
|