需求:问题需要
问题
$\tt A$ 是 $\tt B$ 的亲戚,$\tt B$ 是 $\tt C$ 的亲戚,那么 $\tt A$ 是 $\tt C$ 的亲戚,给出若干个这样的关系,问某两个人是亲戚吗?
思考
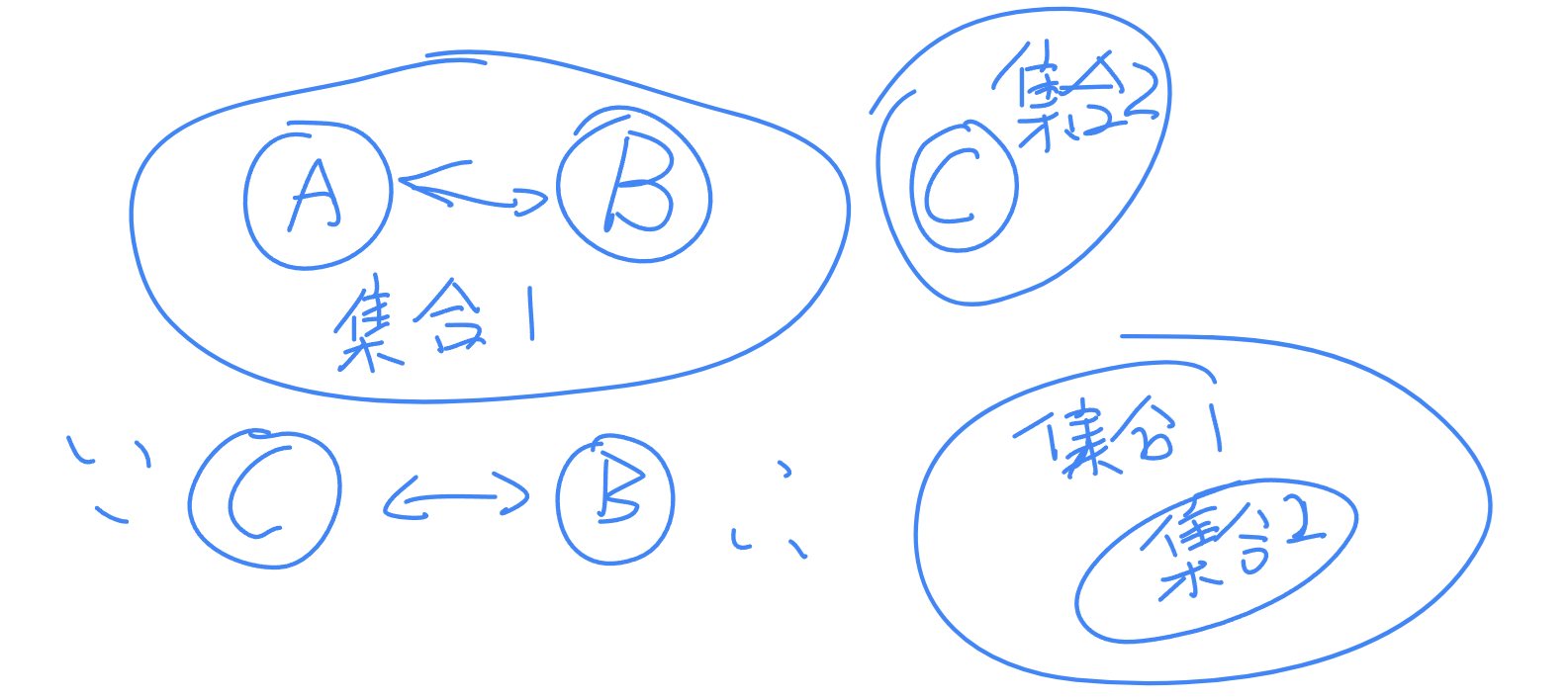
想要实现这样的关系,我们可以先不往算法的方向想,我们可以想如果这是小学数学题你怎么办,考虑如下几种情况:
这样就是我们要说的并查集的基本原理了,只不过写成代码还有亿点点路程,让我们继续推
想要实现这样的功能我们为什么不用 $\tt set$ 集合呢,似乎比我们想要的还要更加直观。当然不行,$\tt set$ 的本质也是树啊(,而且如果我在这个并查集上面要带权值呢(
所以我们这就是要用树形结构,思路也很好懂,比如说我这个 $\tt A$ 是 $\tt B$ 的亲戚,我就可以把 $\tt A$ 的父亲设为 $\tt B$ 这样的操作。
概念
并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
编写:实现思想
基础思路
用刚刚的思路就可以写出如下代码:
1 | int fa[N]; |
但是,上面的代码有个显而易见的漏洞。
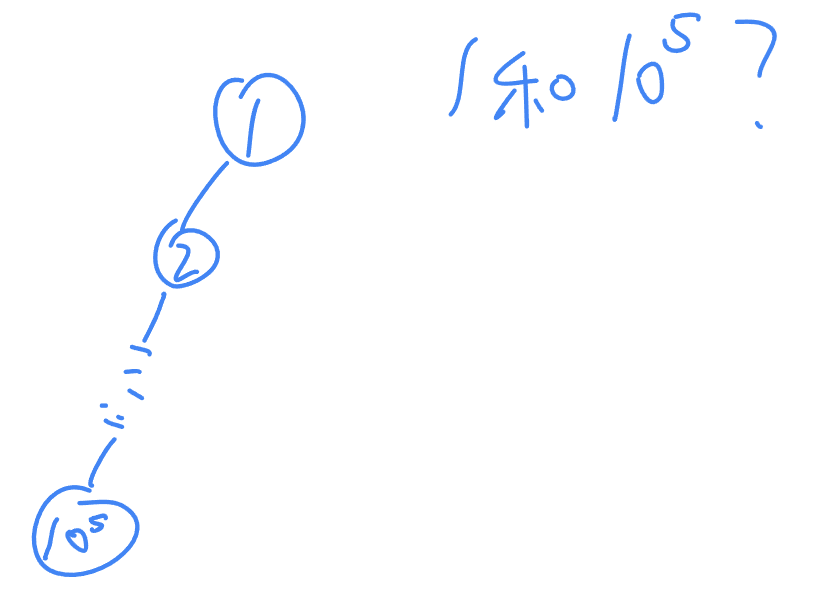
如果我直接把它变成一条链,并且一直访问两短的元素……显而易见退化成O(n)了,这是大大滴不允许滴!
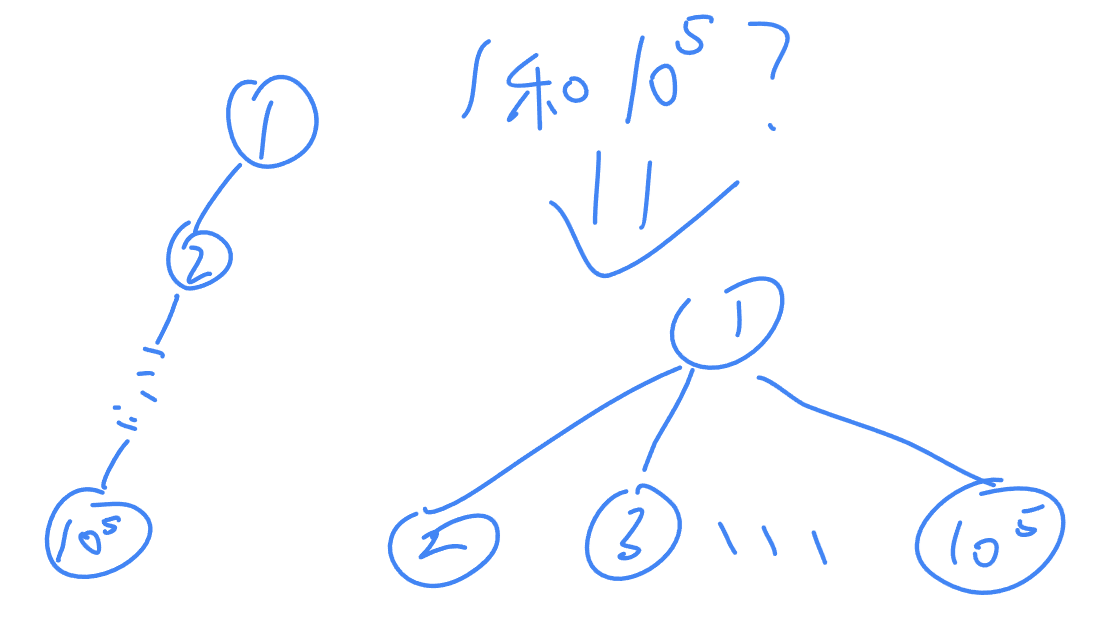
所以我们要把它进化一下,我们可不可以再查找的过程中做手段使得第一次访问整理出答案然后之后直接返回根呢?完全可以,而且我们还可以把我们找到路径上的点的父亲都变成树的根。代码如下
1 | int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); } |
这一个 fa[x]= 就集结了类似于 $\tt DP$ 记忆化的高级精髓,对于刚刚一条链的数据,我们只需要进行一次操作就可以破坏它一条链的结构,如下图
封装代码
1 | const int N = 1e5 + 10; |
实践:并查集经典例题
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 祝馀宫!
评论