算法简介：鱼龙沉四方

$\tt Manacher $ 算法，也叫马拉车；是一个用于求字符串中最大回文子串的算法。相同于 KMP，$\tt Manacher$ 也是一种基于字符串的自动机，他们的本质都是基于已知信息来求出未知信息解决问题。而从实现上来讲，$\tt Manacher$ 算法更加相似于拓展 KMP，到时候慢慢推出来就知道了。

友情链接：

【算法介绍】拓展KMP（Z函数） | 祝馀宫

算法小引：赫赫雷涌起

我们首先从这个算法最最基础的模板开始：P3805 【模板】manacher - 洛谷 | 计算机科学教育新生态
题目的意思很简单，要我们求一个字符串的最长回文子串。

那么首先考虑暴力，这里提一嘴，发现了一个很有趣的现象：同样是 $O(n^3)$ 的暴力，如果我们优先计算较短的回文串这题只能拿十八分，但是如果优先计算较长的回文串，答案会是原来的两倍也就是三十六分！这里贴上两次的代码以方便比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 18pts
inline void Work() {
    int n = strlen(s + 1), ans = 0;
    for(int len = 1; len <= n; len++) {
        for(int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            if(Check(l, r)) {
                ans = max(ans, len);
            }
        }
    }
    printf("%d\n", ans);
}
// 36pts
inline void Work() {
    int n = strlen(s + 1);
    for(int len = n; len >= 1; len--) {
        for(int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            if(Check(l, r)) {
                printf("%d\n", len);
                return ;
            }
        }
    }
}

那么基本上来做这道题的都不算特别差，我们肯定还会有 $O(n^2)$ 的做法，什么？你不会？OK，我们再来看看 $O(n^2)$ 应该是什么姿态。

众所周知，回文串一定是以正中间为对称轴然后向两边拓展的（所谓正中间，就是奇数长度回文串中间字符或者偶数长度回文串中间两个字符的中间）但是说呢，两个偶数之间的字符是一个不存在的，如果我们要枚举他会特别麻烦，于是呢，我们有一种取巧的手法，也是 $\tt Manacher$ 算法中的一个重要思想：插入字符。

比如说题目规定了这次的字符串只包含小写字母，那么我们插入的字符就可以使用大写字母，但是不建议。总而言之插入的字符必须得是题目给出字符串所没有的，一般来讲呢，我们有一个不成文的规定，就是插入 # 。我也不知道为什么，我从刚刚学 $\tt Manacher$ 的时候老师就这么叫我，去看题解区也都是全用 #

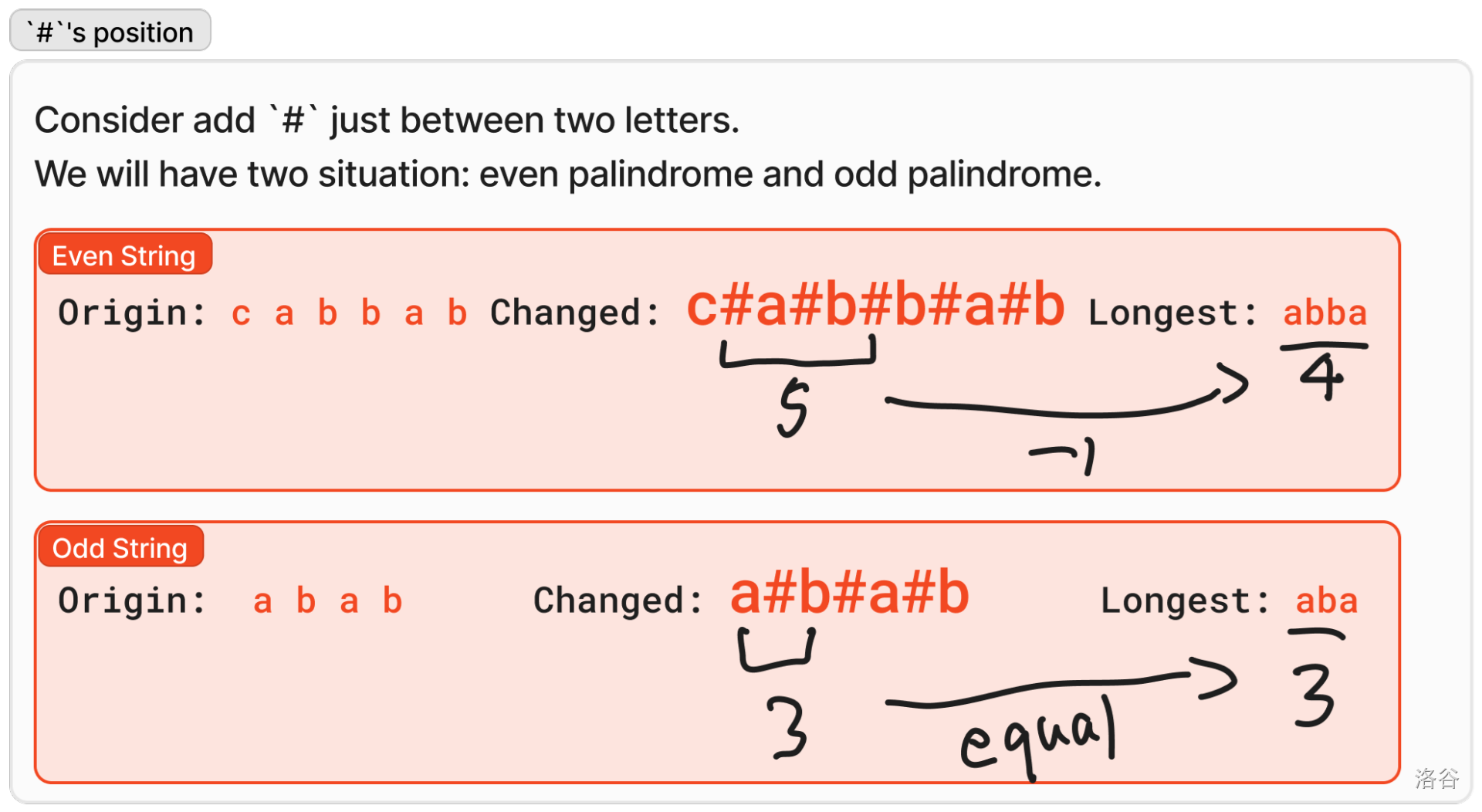
但是说呢，我们肯定不能只在缝隙里插，我们可以考虑一下下面这两种串的变化：

对于只在缝隙里插入字符的情况

然后呢说，这其实也证明了如果只在字符之间插入特殊字符的话，是无法区分奇数回文串和偶数回文串的，这样肯定是挂的，所以说为了统一答案，我们还要在字符串两边插入特殊字符，不信的话把这样改过的字符串代到上面试试。

1
2
3
4
5
6
7
8
9
inline void Change() {
    s[0] = '~'; s[1] = '#'; 
    // s[0] 我自有用处，到时候慢慢看
    for(int i = 1; i <= n; i++) {
        s[i * 2] = t[i];
        s[i * 2 + 1] = '#';
    }
    n = 2 * n + 1; s[n + 1] = '\0';
}

那么在这之后，我们就只需要向外拓展就可以，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
inline void Work() {
    Change(); int ans = 0;
    for(int i = 1; i <= n; i++) {
        int now = 0;
        while(s[i - now] == s[i + now]) now++;
        // 因为设置了字符串两端的特殊值，所以说不会越界，这就是 s[0]='~' 的原因
        ans = max(ans, now);
    }
    printf("%d\n", ans - 1); // 自己模拟去，减一的本质是
    // 像刚刚那样偶数回文串半径和答案是减一关系
    // 但是奇数回文串在被填充了之后翻了一倍的长度也变成了偶数，所以也得减一
}

这样的复杂度最大是 $O(n^2)$ 相对来说非常优秀，在这题可以拿 66pts 的好成绩

算法推导：潮奔蓦引电

其实走到了这一步，答案已经越来越接近于真确的马拉车算法了。那么这个做法的问题是显然的，他枚举了过多重复状态，这是不允许的。也就是说优化掉重复状态。那么优化的思路其实也和拓展KMP差不多，就是寻找重叠状态，我们可以有如下思考：

  • 对于一个回文串，有且仅有一个对称中心。且叫它回文对称中心。
  • 在一个回文串内，任选一段子串 $\operatorname X$ ，一定存在关于“回文对称中心”对称的一个子串 $\operatorname Y$ ，且把这个子串 $\operatorname Y$ 叫做关于子串 $\operatorname X$ 的对称子串。
  • 若一个子串 $\operatorname X$ 存在一个对称子串 $\operatorname Y$ 是回文串，这个子串 $\operatorname X$ 必定是一个回文串。在包含他们的大回文串内，它们回文半径相等。
  • 于是说我们通过确定关系预先得到的回文半径，它的数值，必定小于等于这个位置真实的回文串半径。

那么一样的，我们如果存下了一个右端点最靠右的回文串，那么所有右端点小于它的点，我们都可以通过上述对称关系得到。如果当前点在范围 $[mid,r]$ 内（$mid$ 和 $r$ 是记录的右端点最靠右的回文串的回文对称中心和右端点）那么我们一定可以找到当前点在这个回文串内的对称点，且这个点的位置是 $mid\times2-i$（这个很容易得到，设对称点位置是 $j$ 那么一定存在 $(i+j)\div 2 = mid$ 自行整理可得结论）

然后呢我们知道，通过这个右端点我们所能得知的最右边范围是 $r$ 也就是说我们存在式子 $i + d-1\le r$（其中 $d$ 是回文串的半径）于是得到 $d\le r-i+1$ 答案和刚刚算出来的对称点最长回文串取 $\operatorname{min}$ 即可。

这就是 $\tt Manacher$ 算法的主要思想，就是通过回文对称把未知点对称到已知点，从而通过以前的答案推出当前答案。

对了，再用上面的求完后，还需要 while 拓展看一看能不能拓展，和拓展KMP一个道理

算法模板：牵星觅乡岸

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void Manacher() {
    ll mx = 0, pos = 0; // mx 是上文的 r，pos 是上文的 mid
    for(int i = 1; i <= n; i++) {
        // 由于总是会向右枚举，所以当前点一定大于mid
        if(i <= mx) len[i] = min(len[2 * pos - i], mx - i + 1);
        else len[i] = 1; // 无关紧要
        while(s[i - len[i]] == s[i + len[i]]) {
            len[i]++; // 和刚刚一样，由于在 s[0] 和 s[n+1] 设置了与众不同的值，所以说不会越界
        }
        if(i + len[i] > mx) {
            mx = i + len[i] - 1;
            pos = i;
        }
    }
}

算法演示：踏浪霞连阶

那么一样的来一道例题试试水，出门左转：P4555 国家集训队 最长双回文串 - 洛谷 | 计算机科学教育新生态

显然的这道题求最长的由两个非空回文串组合起来的字符串。那么正常的 $\tt Manacher$ 肯定是不可以的，于是说我们要做出适当的变化。如果我们直接的求两个回文中心拼凑，显然不好实现。于是乎，我们就可以适当变通，如果我们记录了一个以某一个点结尾，或者以某一个点开始的最长回文子串，那么答案就变得好处理了。那么马拉车算法求的是以某一个点为中心往外拓展的最长回文子串，我们只要求出这个回文子串的左右端点就可以知道这个信息。

基本上是这个思路，但是有一个细节在代码里见

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
// copied from solution
#include <bits/stdc++.h>
#define ll long long
#define space putchar(' ')
#define endl putchar('\n')
#define debug puts("------------------------")
using namespace std;
inline void read(int &a) {a = 0; int c = getchar(), b = 1; while (c > '9' || c < '0') {if (c == '-')b = -1; c = getchar();} while (c >= '0' && c <= '9') a = (a << 3) + (a << 1) + c - 48, c = getchar(); a *= b; }
inline int  Rem() {int a = 0, c = getchar(), b = 1; while (c > '9' || c < '0') {if (c == '-')b = -1; c = getchar();} while (c >= '0' && c <= '9') a = (a << 3) + (a << 1) + c - 48, c = getchar(); return a *= b; }
inline void write(int x) {if (x > 9)write(x / 10); putchar('0' + x % 10);}
inline void W(int x) {if (x < 0) {putchar('-'), x = -x;} write(x);}
/**/
const int N = 11000005;
char a[N], s[N << 1];
int n, hw[N << 1], ans, l[N << 1], r[N << 1];
/**/
void Pre()//非常模板的插入
{
	s[0] = '#';
	s[1] = '$';
	int cnt = 1;
	for (int i = 1; i <= n; i++)
	{
		s[++cnt] = a[i];
		s[++cnt] = '$';
	}
	n = (n << 1) + 2;
	s[n] = '~';
}

void work()//同样非常模板的Manacher
{
	int mr = 0, mid;
	for (int i = 1; i <= n; i++)
	{
		if (i < mr) hw[i] = min(hw[(mid << 1) - i], mr - i);
		else hw[i] = 1;
		while (s[i + hw[i]] == s[i - hw[i]]) ++hw[i];
		if (hw[i] + i > mr) mr = hw[i] + i, mid = i;
		/**
		 * l[i]表示以i为左端点的最长的回文串
		 * r[i]表示以i为右端点的最长的回文串
		 *
		 * 对于蒟蒻(我)来讲有点抽象所以我们举一个生动的栗子：
		 *
		 * 		首先，字符串为ababaccd
		 *
		 * 				  0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17
		 * 		插入后变成 #|$|a|$|b|$|a|$|b|$|a |$ |c |$ |c |$ |d |~
		 *
		 * 		显然i = 4时,hw[4] = 4
		 * 		L = 7 = i + hw[4]-1;
		 * 		R = 1 = i-hw[4]+1;
		 * 		回文串实际长度=hw[4]-1;
		 * 		所以转移就是: l[i+hw[i]-1]=max(l[i+hw[i]-1],hw[i]-1);
		 * 					 r[i-hw[i]+1]=max(r[i-hw[i]+1],hw[i]-1);
		 *
		 */
		r[i + hw[i] - 1] = max(r[i + hw[i] - 1], hw[i] - 1);
		l[i - hw[i] + 1] = max(l[i - hw[i] + 1], hw[i] - 1);
	}
}

int main()
{
	scanf("%s", a + 1);
	n = strlen(a + 1);
	Pre();
	work();
/**
 *	又因为两块不能重叠，所以我们选择'$'作为断点进行枚举
 *
 *  那么先提出一个困扰蒟蒻我的问题：
 * 
 *	Q: 上面不是已经求过了吗，为什么还要递推呢？
 *
 *  A: 上面求出的每个l[i]和r[i]都是在i最大的情况下求的
 *  	
 *  	eg:0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17
 *		   #|$|a|$|b|$|a|$|b|$|a |$ |c |$ |c |$ |d |~
 *
 * 		l[3]求出来的是0,但很明显bab是一个回文,l[3]应该等于3
 * 		这是因为我们在i=6时,hw[i]=6,只更新了l[1]和r[11],因为bab不是i=6的最长回文串所以没有更新
 *
 * 		这时就需要递推把前面的转移过来了：
 *
 * 			bab 比 ababa 短两个字符。
 * 			每一个回文串向后挪动一个 都会少两个字符,所以：
 * 		 	l[i] = max(l[i], l[i - 2] - 2);
 * 			r[i] = max(r[i], r[i + 2] - 2);
 * 			我们枚举的是'$'的位置，所以l[i]正推由前一个'$'的位置转移来,r[i]逆推由后面的'$'转移来，每次都会-2回文串长度
 *
 */
	for (int i = n; i >= 1; i -= 2) r[i] = max(r[i], r[i + 2] - 2);
	for (int i = 1; i <= n; i += 2) l[i] = max(l[i], l[i - 2] - 2);

	for (int i = 1; i <= n; i += 2) if (r[i] && l[i]) ans = max(ans, l[i] + r[i]);
	W(ans);
	return 0;
}

算法实战：北斗祓幽孽

查看相关算法标签喵！

参考资料（以下排名不分先后）

  1. 题解 P3805 【【模板】manacher算法】 - 洛谷专栏
  2. 题解 P4555 【国家集训队 最长双回文串】 - 洛谷专栏
  3. Manacher - OI Wiki