算法简介：林雾间的行迹

上次的图论差不多研究完了，这次就打算开一个新的专题。本来是想着动态规划来着，正巧有一个什么活动，让我们整一个笛卡尔树的算法学习笔记，那我就略略研究了一下，写下来的专题不出意外我都会写一些树状树形结构，尤其是二叉搜索树这一类的，可以去看博客里的二叉搜索树标签。（马上要 noip 了，更新不会太快）

刚刚也说了，笛卡尔树其实是一种二叉搜索树的结构，二叉搜索树的概念还没有讲过，估摸着后面会和平衡树的时候一起系统的介绍。而笛卡尔树作为二叉搜索树的一个分支内容，自然是有着二叉搜索树的特殊性质，我们的副标题也提到他是二叉搜索树中的小根堆，这是为什么呢？且听下文分解。

算法演示：藏蜜酒的王蜂

基本概念：栖地蝠的灵笼

首先我们要讲笛卡尔树，来先讲讲二叉搜索树的基本概念。所谓二叉搜索树，就是对于这棵树上所有的节点，他的左子树的所有节点都小于该节点，他的右子树中的所有点都大于该节点。特殊的，空树也是一个二叉搜索树。

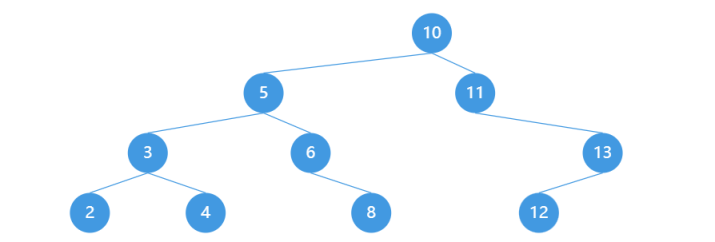
举一个二叉搜索树的例子：

二叉搜索树实例

显而易见的，这是一个非常规范的二叉搜索树。这里给出一个二叉搜索树的可视化生成网站，可以更加直观的理解二叉搜索树。我们可以先模拟一下二叉搜索树的过程。这里我首先设置了根节点：10 。

然后我们插入 5 ，不难发现，5 < 10 ，所以说我们放在 10 的左儿子上。然后插入 3，一路递归下去，3 < 10 去左子树，3 < 5 去左子树，然后就有了现在的 3。其他都差不多，二叉搜索树的构建过程，其实就是我们从根节点出发，不断通过判断插入元素小于或者大于当前的节点，然后去左右子树继续搜索，直到找到一个叶子节点的位置，把插入节点放进去。

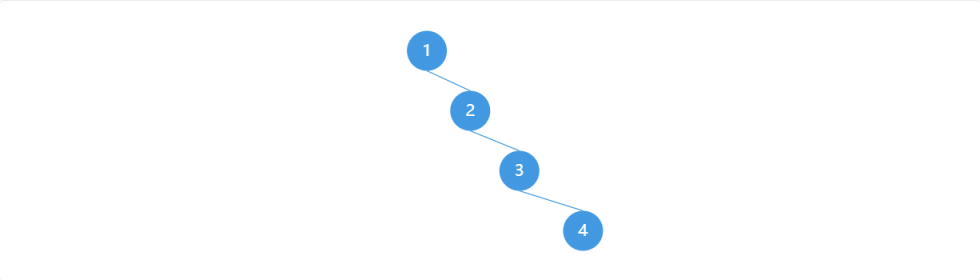
不难发现，二叉搜索树有一个很大的缺陷：会退化成链！什么情况会这样呢？显而易见的，我们如果按照顺序插入节点，也就是根为 1，然后插入 2，3，4，等等等等，这时候，我们的二叉搜索树会是下面这样的：

退化成链的二叉搜索树

这也是二叉搜索树的一大痛处，非常不具备平衡性，也就是说容易退化成链，想要修改这样的错误，就需要用到平衡树的内容了，不是这篇文章该讲的，点到为止。

这里我们可以看出，其实二叉搜索树的中序遍历的结果，就是一棵树所有元素排序后的结果（这个是真的不难证明）

笛卡尔树：如夜风的谜烟

我现在来说一下，笛卡尔树，首先澄清一下，笛卡尔树和笛卡尔的关系，就像雷峰塔和雷锋一样，没有任何的关系。至于他为什么叫做笛卡尔树，我也不知道，咱也问不了（~~可以考虑考虑去过去的欧洲看看~~

首先介绍一下笛卡尔树的概念，副标题中的二叉搜索树中的小根堆，其实就道出了笛卡尔树的两个特点：二叉搜索树和小根堆。先给出一个笛卡尔树的常见图片：

笛卡尔树

先看看为什么是二叉搜索树，从上图可以观察到一个性质（好吧你的观察能力真强）每一个节点上面都有一个虚线对到上面数组里的元素。不难发现这些点从左到右都是按照顺序排列的，这就是笛卡尔树的性质之一，中序遍历的结果，就是原序列。准确的来讲，我们设数组下标为建值 $k$ ，那么笛卡尔树就是一个基于键值 $k$ 的二叉搜索树。

其次呢，我们看为什么是小根堆，这个很显然，我们发现每一个点都是它所在子树中权值最小的点，也就是小根堆的性质，而这里的权值，就是原数组中这个元素的值。所以说，我们可以得到第二个性质，设数组原数为键值 $w$ ，那么笛卡尔树就是一个基于 $w$ 的小根堆。

这时候我们得到了笛卡尔树的定义：

笛卡尔树有两个键值 $(k,w)$
笛卡尔树就是一个基于键值 $k$ 的二叉搜索树
笛卡尔树就是一个基于 $w$ 的小根堆。

注意，笛卡尔树的键值其实是可以根据情况变化的，并不是只能是数组下标或者数组元素，也算是随需求而定的一个灵活算法。

那么我们已经知道了笛卡尔树的概念，我们该如何维护它呢？也就是说如何建出笛卡尔树呢？

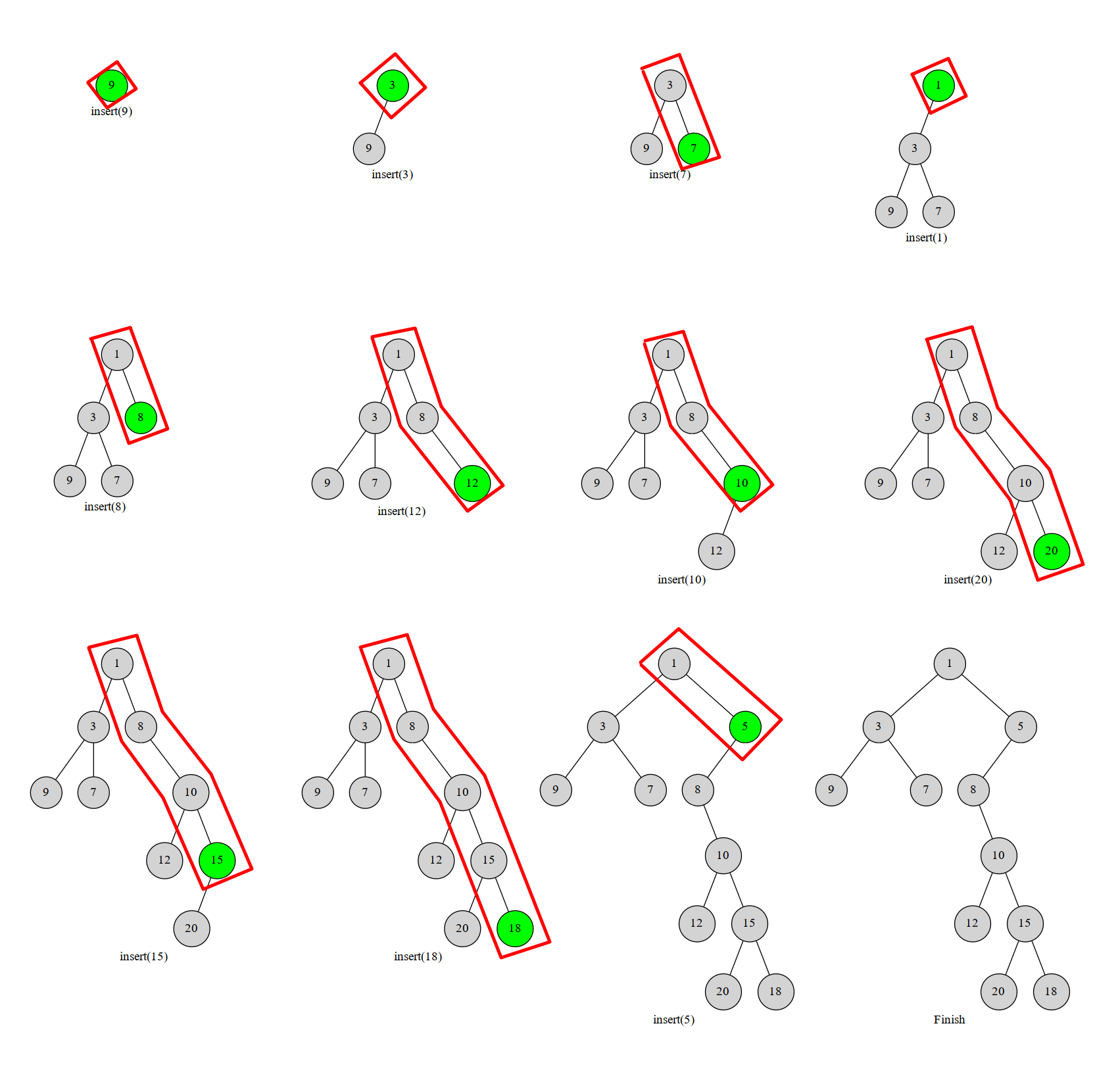
首先我们来看一组关于普通大根堆的插入元素过程：

大根堆的插入

我们发现，其实这个过程就是插入了一个元素，然后在更据他的大小不断地把点向上调整（让然也有向下调整的）这时候，我们在考虑一下笛卡尔树的性质，它需要同时保证一个树，同时满足二叉搜索树和小根堆，我们首先考虑满足二叉搜索树。也就是说，我们的下标时时刻刻都要满足中序遍历的结果是顺序的。这时候就有些点考验想象能力了。

那么我们如果是按照序列的顺序插入点的话，后插入的点下标一定大，这是毋庸置疑的。那么这时候要保证他在中序遍历的结果是这个点在最后一个，不难想到就是把它放在最最最右边，这样就可以保证他在最后面了。那么根据小根堆的性质，我们肯定就要把它向上移动。

向上移动的过程其实就是一路向上，找到大于一个大于它的节点，他的父亲比这个插入的节点小，这时候，别忘了还要维护二叉搜索树，所以说，就把下面的一整个子树，都变成当前节点的左子树就可以了。

干说有点繁杂，我们给出一个图示：

笛卡尔树的插入

红色框框就是我们上面说的插入点维护的，最最右边的内容。其实这就是一个栈结构，也算比较好理解。

算法实现：为心魂的献礼

那么基本的思路都已经想好，我们可以来看看这个东西怎么实现了。

// Copied from OI-wiki (have a little change)
// stk 维护笛卡尔树中节点对应到序列中的下标
for (int i = 1; i <= n; i++) {
  int k = top;  // top 表示操作前的栈顶，k 表示当前栈顶
  while (k > 0 && w[stk[k]] > w[i]) k--;  // 维护右链上的节点
  if (k) rs[stk[k]] = i;  // 栈顶元素.右儿子 := 当前元素
  else root = i; // 退到底了，那么他就是根
  if (k < top) ls[i] = stk[k + 1];  // 当前元素.左儿子 := 上一个被弹出的元素
  stk[++k] = i;                     // 当前元素入栈
  top = k;
}