算法简介:晨露浮光之思
首先声明一点:这篇文章所谓 “连通分量” 并不是指一个算法,而是指算法 $\tt Tarjan$ 和 $\tt Kosaraju$ 算法,他们所应用的点双连通分量,边双连通分量,强连通分量,割点和桥,以及缩点。
我个人认为,$\tt Tarjan$ 算法只是一个思想,他的核心在于定义 $\tt low$ 和 $\tt dfn$ 数组的一系列性质的应用,还有在处理这些数据的过程中处理别的数据。接下来我们会依次介绍这些东西是怎么求的。
算法演示:千式齐聚之法
Tarjan算法:真正的宝物
我们在这里简单的介绍一下 Tarjan 的一个思想。
他首先对于一张图做 Dfs,得到的顺序叫做 Dfs 序,得到的图叫做 Dfs 树。
而对于每一个点被访问的顺序,也就是他第一次被访问的位置,我们用数组 $\tt dfn$ 表示,为什么要这样做呢?我们可以用一张图来简单看一看。我们这里就分为有向图和无向图来看。下图中数字是 Dfs 序。
| 有向图图例 | 边种类介绍 |
|---|---|
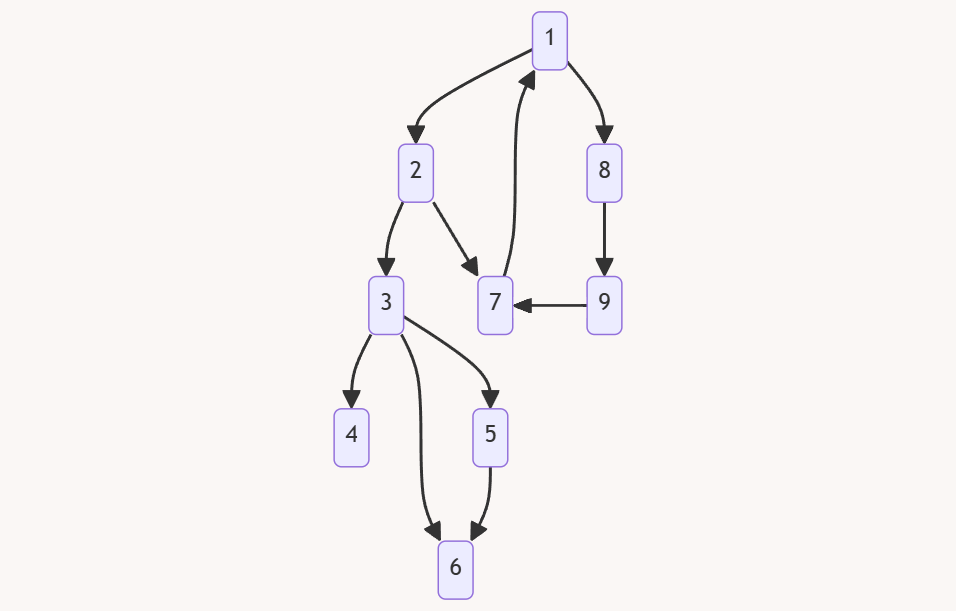 |
我们这样已经把这样的一个有向图变成了 Dfs 树的外观。我们按照这样一颗树的常见形式,将其分为如下几种边: 1. 树 边:这张图中一般的向下的边,都是树边。 2. 前向边:这张图中形如 $3 \rightarrow 6$ 的边是前向边,他们的特征是访问了一个已经标记过的点。 3. 返祖边:这张图中形如 $7 \rightarrow 1$ 的边是返祖边,他们的特征是访问了自己的祖先。 4. 横插边:这张图中形如 $9 \rightarrow 7$ 的边是横插边,他们的特征是访问了一个既不是自己的子孙,也不是自己的祖先的点。 |
不难发现,想要构成环,前向边是没有意义的,因为如果只有树边,前向边的加入不可能构成环,也就是说在做有向图的强连通分量中我们不需要考虑前向边。
| 无向图图例 | 边种类介绍 |
|---|---|
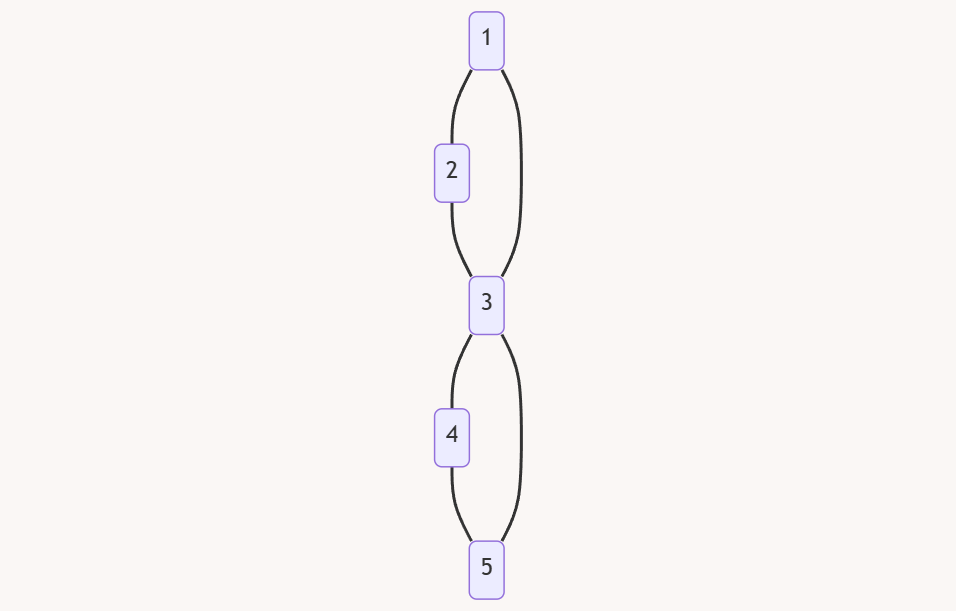 |
我们发现,对于无向图,其实就只有两种边,树边和返祖边。因为如果存在一条不是返祖边的边,我们 Dfs 深搜的性质也会使得它接着往下搜索,也就是说不会存在除了树边和返祖边以外的边。 |
割点:海盗秘宝
首先,我们要知道割点的定义。
对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点(又称割顶)。
—— From 『OI wiki』
说人话:如果把这个点扔掉以后,这个图碎成的块块比原来多,那么这个点就是一个割点。
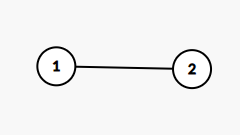
这里给出一个比较奇怪的图:
按照割点的定义,扔掉一个点碎出来的块块比原来的多,那么这里不管扔掉哪一个点,它都是只剩下一块,没有变化,所以这两个点都不是割点。
那么我们知道这是一个针对于无向图的概念,所以说我们应该考虑的是上面给出有向图模型,先把那张图拿回来
那么这样一个图,显而易见这个割点是 3 号点。我们观察一下他有什么特性,不难发现,如果 3 是割点,它两边的子树一定是不连通的,也就是说,如果我们接着Dfs,如果不能走过已经走过点,我们一定无法访问到dfs序比我小的点。如果大力这样判断显而易见复杂度是 $O(n^2)$ 。那么这个想要优化也很简单,我们接着往下搜索的时候记录一个 $\tt low$ 数组,表示不经过已经经过的点所能到达的 dfs 序最小的值。那么这个就很好实现了。
直接上代码(滑稽
1 | int ans = 0; |
点双连通分量:风起风息
我们定义点双连通分量是:把这个图分为没有割点的块块,可以分成的个数。一张没有割点的图我们将其称为点双联通图。
那么既然他是涉及到割点的一个概念,显而易见他还是只能在无向图上面有。
我们想想怎么样才可以找到双连通分量,显而易见的,如果我们把一张图的割点全都断开,碎出来的块块一定没有割点,那么就是点双了。那么我们考虑如何实现。
我们顺着Dfs下去,如果发现了一个割点,说明他下面那个一个子树,是一个点双连通分量,我们要把它分离出来,简单梳理这样的流程发现是这样的结构:
1 | a -> b (Dfs) |
不难发现,,,,这个结构,,,完全符合栈!那么我们就可以用一个栈记录我们走过点,如果发现一个点是割点,就一直退栈,知道找到那个割点,顺便把割点也算到那个连通分量里面。
这样基本上就实现了一个点双连通分量的流程。我们浅浅的看一看代码:
1 | int cl[N], cntc; // 每个点的点双连通分量编号,以及有几个点双连通分量 |
桥:磨刀不误砍柴工
如果说桥,可能不太好理解这个意思,如果换一个法,叫做割边,因该都知道是什么意思了罢。
那么这里给出桥的准确定义:当一个图失去一条边以后,连通分量增加,那么这条边是一条割边(桥)。
那么这个桥的实现本质上和割点没有差太多,我们把 low 数组再改一改,改成不经过已经经过的一条边条边(且这条边不可以是树边的反向边)可以到达的最小 Dfs 序值。那么我们就发现,如果这个点,他不经过树边,也不经过树边的反向边,可以到达的最小的 Dfs 值都比我当前的 Dfs 序值要大,那么这条边就是割边。
注意这里和割点的区别,割点是大于等于,因为如果是割点的话,他如果能到我也没有用,这个割点扔掉了还得断。但是割边不同,如果他能够到我,那就成环了,我断掉也没用,所以说不能等于我,得大于。
这里浅浅的写出实现代码。
1 | vector<pair<int , int > >ans; |
边双连通分量:工作迫近
那么这个边双连通也是一样的。我们只需要找到割边,然后把站里面剩下的点全都挖出来即可,具体实现很简单。
1 | void Tarjan(int u, int fa) { |
强连通分量:麻烦的工作
我们在这里开启新的一篇:强连通分量。
说是新的一篇,是因为这个概念是基于有向图的,所以我们得把一开始给出的有向图模型拿出来。
我们说强连通主打一强连。当一个有向图图它所有节点都可以直接或间接的互相可达(自己到自己除外)这样的图我们称为是强连通的;而强连通分量就是有向图中极大的强连通子图数量。
这样的一个东西我们如何求呢?我们把 low 数组调成最初的模样:不经过已经经过的点可以到达的 Dfs 序最小的点。那么当前这里是一个强连通分量的标志就是 low 值和 dfn 值一样,因为这样相当于我下面的这一块都是到不了我上面的,这一块的点都是我的子孙,而我的子孙又都可以回到我这里,所以这里一定是一个强连通分量,got it。但是这里对于一个走过的点更新 low 的就不一样了,因为有向图他不像无向图只有返祖边,我们这里要记录这个点是否在栈里。
1 | void Tarjan(int u) { |
缩点:善后工作
因为这种有环的乱七八糟的图处理起来非常麻烦,所以缩点的一个作用就是:把一张奇怪的图变成有向无环图。这样就会好做很多,我们只需要对于缩点以后,两个强连通分量的交通存下了去重建新图就可以了,代码很简单,这里不再展示。
1 | Tarjan(1); |
Korasaju 算法:风后宝矿
这是一种基于 Dfs 的算法。具体流程就是,把一个图深搜一遍,然后把他的反图深搜一遍,这样子得到的一块一块的子图,就是强连通分量,实现十分简单,这里不演示。