理论：什么是三分

提到三分，首先就要回顾二分，二分是一种可以在单调函数上寻找值的算法，复杂度 $O(\log n)$ 。

三分与二分不一样的地方是，他把要寻找的值域分为三份，目的是寻找单峰函数的极值。

实现：怎么写三分

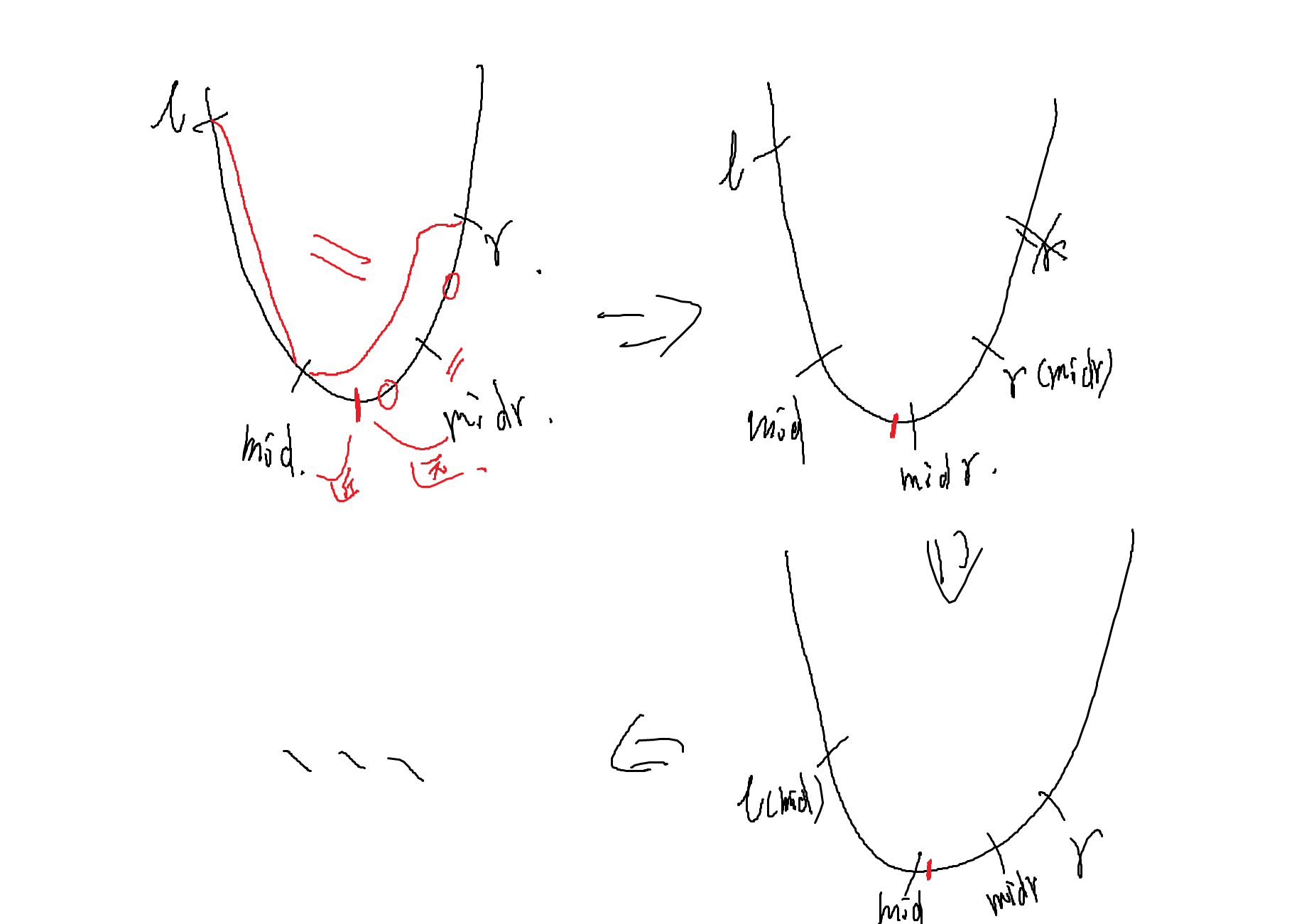
如图：

假设我们要在 $l$ 到 $r$ 中查找最值，先取整个区间的中点。

1
double mid = (l + r) / 2;

然后我们再取右半部分的中点 $midr$

1
double midr = (mid + r) / 2;

然后比较 $mid$ 和 $midr$ 哪个更靠近最值，若 $mid$ 更靠近最值，则舍弃右区间，若 $midr$ 更靠近最值则舍弃左区间。

1
2
3
4
if(Check(mid) > Check(midr))
    r = midr;
else
    l = mid;

完整代码：

1
2
3
4
5
6
7
8
9
10
11
double ssearch(double l,double r){
    while(l+eps<=r){
        double mid = (l + r) / 2;
        midr = (mid + r) / 2;
        if(Check(mid) > Check(midr))
            r=midr;
        else
            l=mid;
    }
    return l; 
}

实践：优质的例题