文章总览：百脉甘津宁神久

李超线段树，是一种维护带斜率的线段信息的线段树，早就听说了，所以今天跑过来填坑了。李超线段树也是属于线段树的变种，主要的应用也就是刚刚说的维护带斜率线段。并且因为他能维护这种特殊的几何结构，也可以用来编写斜率优化DP，所以说也算是比较重要的数据结构了。

下为本文大纲：

  1. 李超线段树推导
  2. 李超线段树模板
  3. 李超树应用基础
  4. 李超数应用斜优

算法推导：壶中洞天云螭眠

  • 李超线段树推导

主要思想：云吟

那么刚刚也说了，李超线段树就是一种维护带斜率的线段的线段树，一般来说查询的都是在一条垂直于 $x$ 轴的是线上我们插入的线段与其的交点中最顶端（纵坐标最大）的那一个。

很显然，我们对于每一个节点，只需要存储我们查询的时候的答案（我们将其称之为优势线段）即可。现在的问题是如何快速处理这个所谓的优势线段。

不难想到分类讨论处理插入的情况。如果插入的情况搞定了，查询就是易如反掌。

基础结构：雷音

有了大概的思路，我们可以考虑以什么样的载体来存储这个李超线段树。很显然我们面对的是一个非常大的区间，毕竟每个线段的左右端点可以到 $x$ 轴很远很远的地方，那么这种时候我们就只有一种选择：离散化和动态开点。

由于是动态开点的话，我们就并不需要建树，直接开始考虑插入和查询的逻辑即可。很显然，直接维护每一个点的优势线段是不现实的，所以我们这里线段树每一个节点维护的是能完全覆盖该区间的线段中的优势线段。

首先从最重要的插入入手，考虑线段树维护的区间与插入线段的关系：

  1. 区间与线段不相交：没变化
  2. 区间与线段有交集，但不包含：继续递归
  3. 区间与线段包含：分为三类
    • 该线段全面碾压了这个区间的优势线段：线段可以作为整个区间的优势线段
    • 该线段被这个区间的优势线段全面碾压：不用管它
    • 与原来的优势线段有交点：递归处理

可以分别对应下面的几种情况：

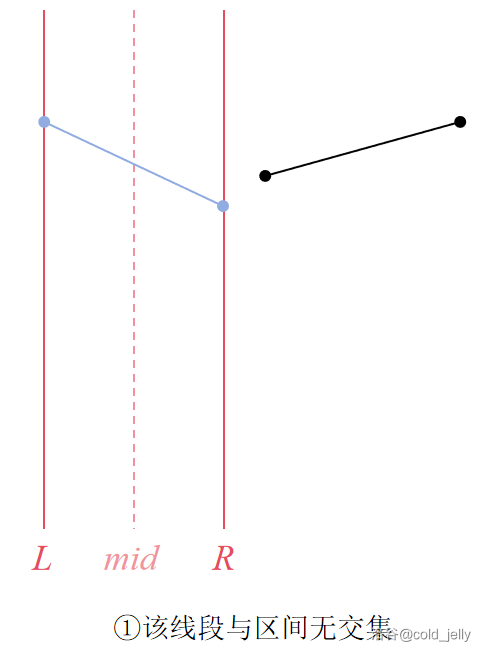
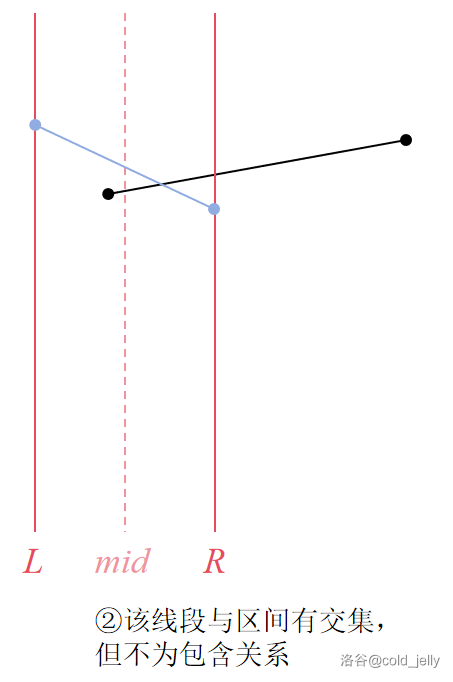
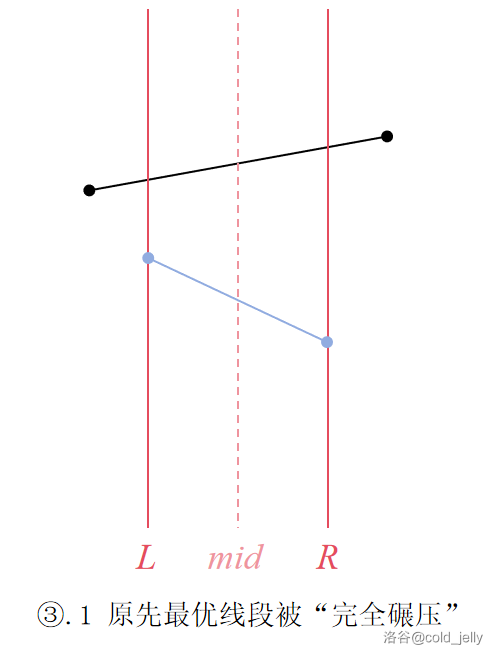
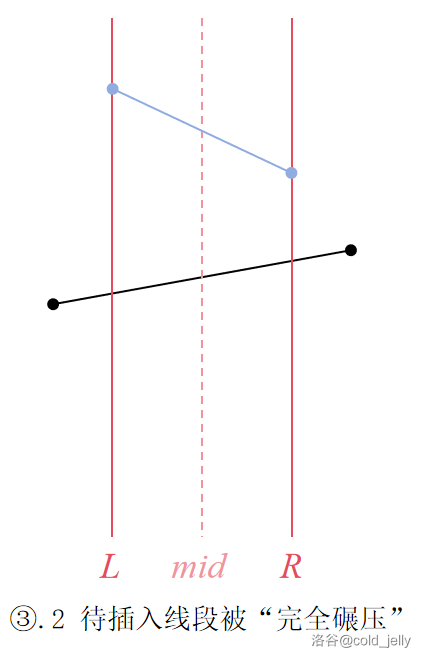
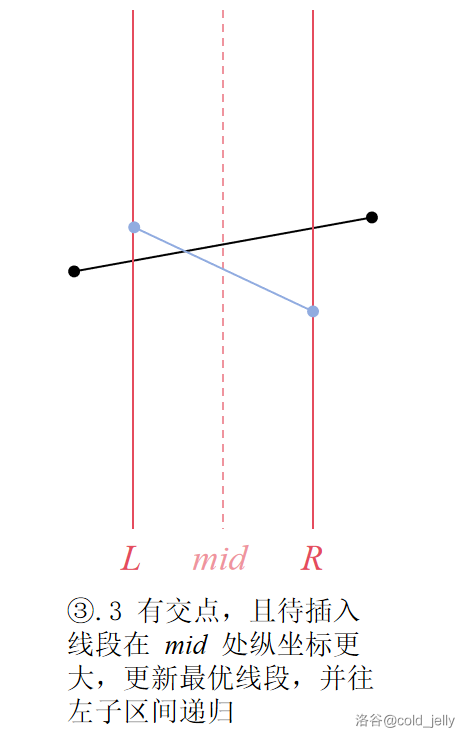
查询操作相比起来就没有技术含量，因为我们已经在插入的过程中维护了每个区间的优势线段，所以说最后我们只需要从根查到这个点一路上记录这些线段到底哪条最优秀即可。

细节推敲：灵引

其实主要的思路在刚刚已经说完了，接下来我要说的就是可能关于代码方面的细节和问题。首先根据刚刚的思路可以写出下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void insert(Node* &p, int l, int r, int id) {
    if(line[id].r < l || r < line[id].l) return ;
    if(p == nullptr) p = new Node();
    int mid = l + r >> 1;
    if(line[id].l <= l && line[id].r >= r) {
        if(cmp(id, p->id, l) && cmp(id, p->id, r)) { p->id = id; return ; }
        if(cmp(p->id, id, l) && cmp(p->id, id, r)) { return ; }
        if(cmp(id, p->id, mid)) swap(id, p->id);
        if(cmp(id, p->id, l)) insert(p->lc, l, mid, id);
        if(cmp(id, p->id, r)) insert(p->rc, mid+1, r, id);
        return ;
    }
    if(line[id].l <= mid) insert(p->lc, l, mid, id);
    if(mid < line[id].r) insert(p->rc, mid+1, r, id);
}
void query(Node *p, int l, int r, int pos, ll &ans) {
    if(p == nullptr || pos < l || r < pos) return ;
    if(cmp(p->id, ans, pos)) ans = p->id;
    if(l == r) return ;
    int mid = l + r >> 1;
    if(l <= mid) query(p->lc, l, mid, pos, ans);
    if(mid < r) query(p->rc, mid + 1, r, pos, ans);
}

由于我们再插入函数中做了非常多的分类讨论，想要一次性分清这些东西也是十分困难的，接下来我们对这个插入函数简单的做一个逐行的解析：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void insert(Node* &p, int l, int r, int id) {
    // 首先判断线段与区间有没有交集，没有就直接返回
    if(line[id].r < l || r < line[id].l) return ;
    // 访问到了空节点，新建一个（动态开点基本操作）
    if(p == nullptr) p = new Node();
    int mid = l + r >> 1; // 计算中点
    // 如果该区间被线段的定义域完全覆盖
    if(line[id].l <= l && line[id].r >= r) {
        // 区间原本的优势线段被全方位碾压
        if(cmp(id, p->id, l) && cmp(id, p->id, r)) { p->id = id; return ; }
        // 插入的线段被优势线段全方位碾压
        if(cmp(p->id, id, l) && cmp(p->id, id, r)) { return ; }
        // 接下来就是有交点的情况
        // 这里中点判断的含义是，这个插入线段在中点部分是优势的话，那么至少大于一半的部分属于优势了
        // 而原本的这个优势线段，由于我们并不知道他是左边部分优还是右边部分优，所以下传更新
        if(cmp(id, p->id, mid)) swap(id, p->id);
        // 左边优势
        if(cmp(id, p->id, l)) insert(p->lc, l, mid, id);
        // 右边优势
        if(cmp(id, p->id, r)) insert(p->rc, mid+1, r, id);
        return ;
    }
    // 常规操作
    if(line[id].l <= mid) insert(p->lc, l, mid, id);
    if(mid < line[id].r) insert(p->rc, mid+1, r, id);
}

所以说可以注意到，我们存储在这个所谓维护整个区间的线段，其实也是有无法确定的时候，在当一个区间内有多个优势线段的时候我们这样就错误了，所以说查询我们是要从根一直到这个点中最优势的优势线段。

代码比较简单，不解释了。

另外还有一个很抽象的问题，由于我因为 sgn 写错出了大锅，所以贴一下 sgn 的代码：

1
inline int sgn(double x) { return fabs(x) <= eps ? 0 : (x > eps ? 1 : -1); }

接下来看关于李超线段树的一个拓展用法。

额外拓展：悬印

另外是关于李超线段树的合并，其实和正常的差不多，直接贴代码了：

1
2
3
4
5
6
7
8
9
10
Node* merge(Node* u, Node* v, int l, int r) {
    if(!u) return v;
    if(!v) return u;
    insert(u, l, r, v->id);
    int mid = l + r >> 1;
    u->lc = merge(u->lc, v->lc, l, mid);
    u->rc = merge(u->rc, v->rc, mid+1, r);
    delete v;
    return u;
}

这个也没什么好解析的，然后我们来看一个总体的模板。

基础模板：掌间乾坤便通玄

  • 李超线段树模板

这个就是李超线段树总体模板。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
const double eps = 1e-8;

struct Line {
    ll l, r;
    double k, b;
    Line(ll l=0, ll r=0, double k=0, double b=0) : l(l), r(r), k(k), b(b) {}
    // Calc l,r,k,b from (ax, ay)&(bx,by)
    Line(ll ax, ll ay, ll bx, ll by) {
        if(ax > bx) swap(ax, bx), swap(ay, by);
        l = ax, r = bx;
        if(ax != bx) {
            k = 1.0 * (by - ay) / (bx - ax);
            b = ay - k * ax;
        }
        else {
            k = 0;
            b = max(ay, by);
        }
    }
    inline double f(int x) { 
        return k * x + b; 
    }
}line[N];
int cntl;

inline int sgn(double x) { return fabs(x) <= eps ? 0 : (x > eps ? 1 : -1); }
// check f_i(x) > f_j(x)
inline bool cmp(int i, int j, int x) {
    int t = sgn(line[i].f(x) - line[j].f(x));
    if(t == 0) return i < j;
    return t == 1;
}

struct Node {
    Node *lc, *rc; int id;
    Node(Node* _l=nullptr, Node*  _r=nullptr, int _id=0) : lc(_l), rc(_r), id(_id) { }
};
class LiChaoTree {
public:
    void insert(Node* &p, int l, int r, int id) {
        if(line[id].r < l || r < line[id].l) return ;
        if(p == nullptr) p = new Node();
        int mid = l + r >> 1;
        if(line[id].l <= l && line[id].r >= r) {
            if(cmp(id, p->id, l) && cmp(id, p->id, r)) { p->id = id; return ; }
            if(cmp(p->id, id, l) && cmp(p->id, id, r)) { return ; }
            if(cmp(id, p->id, mid)) swap(id, p->id);
            if(cmp(id, p->id, l)) insert(p->lc, l, mid, id);
            if(cmp(id, p->id, r)) insert(p->rc, mid+1, r, id);
            return ;
        }
        if(line[id].l <= mid) insert(p->lc, l, mid, id);
        if(mid < line[id].r) insert(p->rc, mid+1, r, id);
    }
    void query(Node *p, int l, int r, int pos, ll &ans) {
        if(p == nullptr || pos < l || r < pos) return ;
        if(cmp(p->id, ans, pos)) ans = p->id;
        if(l == r) return ;
        int mid = l + r >> 1;
        if(l <= mid) query(p->lc, l, mid, pos, ans);
        if(mid < r) query(p->rc, mid + 1, r, pos, ans);
    }
    Node* merge(Node *u, Node *v, int l, int r) {
        if(!u) return v;
        if(!v) return u;
        insert(u, l, r, v->id);
        int mid = l + r >> 1;
        u->lc = merge(u->lc, v->lc, l, mid);
        u->rc = merge(u->rc, v->rc, mid+1, r);
        delete v;
        return u;
    }
};

接下来我们看一些关于李超线段树的例题。

简单例题：肘后备急除外障

  • 李超树应用基础

题目大意

在线处理直线 $x=a$ 与若干个一次函数的交点中 $y$ 坐标最大的那一个。

解题思路

模板。

正确代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

const int N = 1e5 + 10;
const double eps = 1e-8;

struct Line {
    ll l, r;
    double k, b;
    Line(ll l=0, ll r=0, double k=0, double b=0) : l(l), r(r), k(k), b(b) {}
    // Calc l,r,k,b from (ax, ay)&(bx,by)
    // Line(ll ax, ll ay, ll bx, ll by) {
    //     if(ax > bx) swap(ax, bx), swap(ay, by);
    //     l = ax, r = bx;
    //     if(ax != bx) {
    //         k = 1.0 * (by - ay) / (bx - ax);
    //         b = ay - k * ax;
    //     }
    //     else {
    //         k = 0;
    //         b = max(ay, by);
    //     }
    // }
    inline double f(int x) { 
        return k * (x - 1) + b; 
    }
}line[N];
int cntl;

inline int sgn(double x) { return fabs(x) <= eps ? 0 : (x > eps ? 1 : -1); }
// check f_i(x) > f_j(x)
inline bool cmp(int i, int j, int x) {
    int t = sgn(line[i].f(x) - line[j].f(x));
    if(t == 0) return i < j;
    return t == 1;
}

struct Node {
    Node *lc, *rc; int id;
    Node(Node* _l=nullptr, Node*  _r=nullptr, int _id=0) : lc(_l), rc(_r), id(_id) { }
};
class LiChaoTree {
public:
    void insert(Node* &p, int l, int r, int id) {
        if(line[id].r < l || r < line[id].l) return ;
        if(p == nullptr) p = new Node();
        int mid = l + r >> 1;
        if(line[id].l <= l && line[id].r >= r) {
            if(cmp(id, p->id, l) && cmp(id, p->id, r)) { p->id = id; return ; }
            if(cmp(p->id, id, l) && cmp(p->id, id, r)) { return ; }
            if(cmp(id, p->id, mid)) swap(id, p->id);
            if(cmp(id, p->id, l)) insert(p->lc, l, mid, id);
            if(cmp(id, p->id, r)) insert(p->rc, mid+1, r, id);
            return ;
        }
        if(line[id].l <= mid) insert(p->lc, l, mid, id);
        if(mid < line[id].r) insert(p->rc, mid+1, r, id);
    }
    void query(Node *p, int l, int r, int pos, int &ans) {
        if(p == nullptr || pos < l || r < pos) return ;
        if(cmp(p->id, ans, pos)) ans = p->id;
        if(l == r) return ;
        int mid = l + r >> 1;
        if(l <= mid) query(p->lc, l, mid, pos, ans);
        if(mid < r) query(p->rc, mid + 1, r, pos, ans);
    }
    Node* merge(Node *u, Node *v, int l, int r) {
        if(!u) return v;
        if(!v) return u;
        insert(u, l, r, v->id);
        int mid = l + r >> 1;
        u->lc = merge(u->lc, v->lc, l, mid);
        u->rc = merge(u->rc, v->rc, mid+1, r);
        delete v;
        return u;
    }
};

int n;

inline void Input() {
    read(n);
}

LiChaoTree Tree; Node *rt;

inline void Work() {
    char s[10]; double S, P; 
    ll T; int ans;
    while(n--) {
        scanf("%s", s + 1);
        if(s[1] == 'P') {
            scanf("%lf%lf", &S, &P);
            // 斜率和截距别填反了
            line[++cntl] = Line(1, 50000, P, S);
            Tree.insert(rt, 1, 50000, cntl);
        }
        else {
            read(T);
            if(cntl == 0) printf("0\n");
            else {
                ans = 0;
                Tree.query(rt, 1, 50000, T, ans);
                if(ans == 0) {
                    printf("0\n");
                    continue;
                }
                ans = (int)((line[ans].b + (T - 1) * line[ans].k) / 100);
                printf("%d\n", ans);
            }
        }
    }
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

经典运用：方定一倾浣俗尘

  • 李超数应用斜优

题目大意

有 $n$ 根柱子依次排列，每根柱子都有一个高度。第 $i$ 根柱子的高度为 $h_i$。

现在想要建造若干座桥，如果一座桥架在第 $i$ 根柱子和第 $j$ 根柱子之间，那么需要 $(h_i-h_j)^2$ 的代价。

在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第 $i$ 根柱子被拆除的代价为 $w_i$，注意 $w_i$ 不一定非负，因为可能政府希望拆除某些柱子。

现在政府想要知道，通过桥梁把第 $1$ 根柱子和第 $n$ 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。

解题思路

首先不难写出转移方程：$dp[i]=\min\{dp[j]+(h[i]-h[j])^2+sum[i-1]-sum[j]\}$。
其中 $sum$ 表示 $w$ 数组的前缀和。

首先把斜率式推导出来是：设 $Y(j)=dp[j]+h[j]^2-sum[j],X(j)=h[j]$，

很显然不论是横坐标 $X(j)$ 还是斜率 $2h[i]$ 都不单调，所以不能通过凸包维护。

那么考虑李超线段树，首先找出最原始的转移方程化简：

由于 $i$ 是我们枚举的，$j$ 却需要从前缀里面寻找，所以说里李超线段树应当维护 $j$ 有关的量。如果把 $-2h[j]$ 看作斜率，$dp[j]+h[j]^2-sum[j]$ 看作截距，我们相当于再求若干个一次函数与 $h[i]$ 交点的最低点。符合李超线段树能维护的类型范畴内。算法非常成立。

正确代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 9;
const int M = 1e6;
const ll INF = 1e18;

struct Line {
    ll k, b;
    Line(ll k = 0, ll b = 0) : k(k), b(b) {}
    inline ll f(ll x) { return k * x + b; }
} line[N];
int cnt;

struct Node {
    Node *lc, *rc;
    int id;
    Node() : lc(nullptr), rc(nullptr), id(0) {}
};

class LiChaoTree {
private:
    // 比较函数：在x处i是否比j更优（值更小）
    inline bool cmp(int i, int j, ll x) {
        if (i == 0 && j == 0) return false;
        if (i == 0) return false; // 空线段不优
        if (j == 0) return true;  // 任何线段都比空线段优
        return line[i].f(x) < line[j].f(x);
    }

public:
    // 插入线段
    void insert(Node* &p, int l, int r, int id) {
        if (!p) p = new Node();
        int mid = (l + r) >> 1;
        
        // 比较当前节点和待插入线段
        if (cmp(id, p->id, mid)) {
            swap(id, p->id);
        }
        
        if (cmp(id, p->id, l)) {
            if (l == r) return;
            insert(p->lc, l, mid, id);
        }
        else if (cmp(id, p->id, r)) {
            if (l == r) return;
            insert(p->rc, mid + 1, r, id);
        }
    }
    
    // 查询最小值
    ll query(Node* p, int l, int r, ll x) {
        if (!p) return INF;
        ll res = (p->id ? line[p->id].f(x) : INF);
        
        if (l == r) return res;
        
        int mid = (l + r) >> 1;
        if (x <= mid) {
            return min(res, query(p->lc, l, mid, x));
        } else {
            return min(res, query(p->rc, mid + 1, r, x));
        }
    }
};

ll h[N], w[N], f[N];
LiChaoTree Tree;
Node *root = nullptr;

int main() {
    int n;
    scanf("%d", &n);
    
    // 初始化0号线段（空线段）
    line[0] = Line(0, INF);
    
    for (int i = 1; i <= n; i++) scanf("%lld", &h[i]);
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &w[i]);
        w[i] += w[i - 1];
    }
    
    // 第一条直线
    cnt++;
    line[cnt] = Line(-2 * h[1], h[1] * h[1] - w[1]);
    Tree.insert(root, 0, M, cnt);
    
    for (int i = 2; i <= n; i++) {
        // 查询最优值
        f[i] = h[i] * h[i] + w[i - 1] + Tree.query(root, 0, M, h[i]);
        
        // 添加新直线
        cnt++;
        line[cnt] = Line(-2 * h[i], f[i] + h[i] * h[i] - w[i]);
        Tree.insert(root, 0, M, cnt);
    }
    
    printf("%lld\n", f[n]);
    return 0;
}

算法实战：龙涎吐哺胜金丹

查看相关算法标签喵！

参考资料（以下排名不分先后）