算法简介：晶片也是一种宝石

这篇文章主要讲的是最短路径算法，从最低级的 Floyd 开始，到支持最长路的 Dijskra 的初级代码及其优化，还有支持负边权的 Bellman-Ford 算法。最短路径问题作为图论中解决大多数问题的基础，可以与很多图论模型混搭，是一个泛用型很强的问题类型。

算法演示：不能少了冲天转转

例一：改良型平衡稳定器

首先，作为多个最短路算法的始祖（可能吧，毕竟这个是基础）一些关于最短路的基础概念都是由 Floyd 算法引导出来的，所以我们首先来讲的算法，就是 Floyd 算法。

首先，我们给定一张图。不管他是无向图还是有向图，我们都可以求最短路。而计算出来的最短路，分为两种：

  1. 求出一个点到所有点之间的最短路 —— 单源最短路
  2. 求出所有点到所有点之间的最短路 —— 全源最短路

那么我们要用的 Floyd 算法，就是求全源最短路的一个最短路算法。试想一下，如果要求我们在 $O(n^3)$ 的时间复杂度内，实现全源最短路，我们会怎么做？不难想到，就是动态规划。

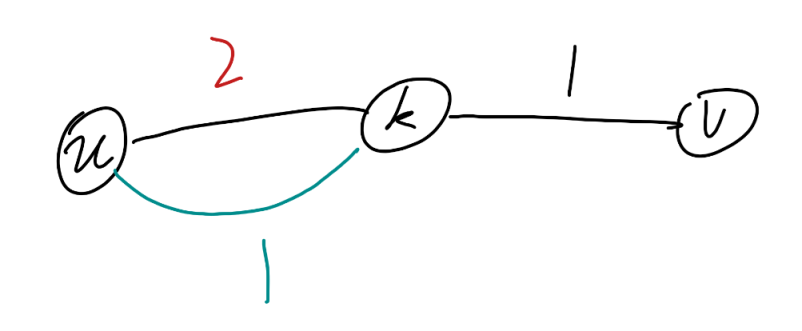
如果我们设置一个状态 $dp[u][v]$ 表示点 $u$ 到 $v$ 的最短路，那么怎么去求最短路呢？ 不难想到，最短路一定是由最短路拼接而成。因为如果最短路上的某一个点到达端点的长度不是最短路，那么一定可以找到一个更短的路径替换掉他。

就像这张图片所展示的，$u\rightarrow k$ 的黑色路径不是最短路，所以说我们可以用青色的路径替换掉黑色路径。也就是说，最短路径一定是由两个最短路径拼接而成。我们可以轻松的写出转移方程：

但是，这个转移方程中 $u,v,k$ 的枚举顺序如何排列？随便排列吗？显然不是。我们要使得 $dp[u][v]$ 被 $dp[u][k]+dp[k][v]$ 转移，我们肯定要保证这个值已经被计算了，不然一定是得不到正确值的。所以说，我们的枚举顺序就可以确定：

1
2
3
4
5
6
7
for(int k = 1; k <= n; k++) {
    for(int i = 1; i <= n; i++) {
        for(int j = 1 ; j <= m; j++) {
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
        }
    }
}

然后就是初始值的设定。首先，自己到自己，都是不需要费用的，设置为 0 ；已知的边，自己设了就可以；其他的显而易见都不知道，设置为极大值。显而易见，这样的动态规划思想对于任何的图都不会有问题。这就是 Floyd 算法的全过程了，其中状态转移的过程，在最短路中被称为松弛操作，这个名词也可能广泛出现于一些动态规划题目中。

Floyd 算法的思想是极其常用的，这种不断松弛的操作思想，有时会出现在一些非图论的动态规划题目中，也算是一本万利的一种算法思想。

例二：敌人越多越要小心

接下来，就是一个重要的算法，也是最常用的最短路算法，Dijkstra 算法。在我的最小生成树文章中，曾经提到过一个名字叫做 Prim 的算法。这个算法与 Dijkstra 算法有着极高的相似度。具体的来讲，两者都是基于贪心去扩大点集合而去计算的一种算法，而这种贪心的思想，就导致了 Dijkstra 算法不可以有负边权，具体为什么我们会在下文讲到。

我们都知道，想要求得最短路，上面的 Floyd 算法中也说了最短路是最短路的拼接，所以说 Dijkstra 算法秉承着这样的思想，我们对于已经保证求得最短路的点，去找到他们之中距离源（开始节点）最近也就是最短路最小的点，从这个最小的点开始，继续往下推，这样就可以保证求出从源开始所有点的最短路。

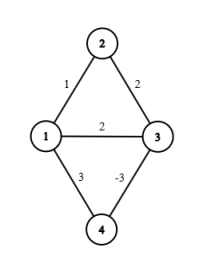
但是说，这样的贪心思想就突显了一个问题，负边权。我们可以举一个例子：

负边权图

显然的，用人脑算出来，1 到 3 的最短路，就是 0 。但是，如果我们按照最短路的思想，我们会先走到 $2$ 求出 $dis[2]=1$ 然后标记掉他，因为每一个点都只能扩散一次，如果没有这个优化，我们会陷入死循环，有一些点永远得不到计算。然后从 $2$ 扩散到 3 ，得到 $dis[3] = 3$ 然后标记了他。这是候重点就来了，他会去跑到四，得到 $dis[4]=0$ 然后结束。因为所有点都已经求好了。然后就发现了 $dis[3]$ 的值其实是错误的。这也是 Dijkstra 为什么不可以求负边权的原因。

那么按照这样的思想，我们不难写出一个朴素版本的 Dijkstra 算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void Dijkstra(int u) {
	for(int i = 1; i <= n; i++) dis[i] = INF;
    dis[u] = 0;
    for(int i = 1; i <= n; i++) {
        int mi = INF, id = 0;
        for(int j = 1; j <= n; j++) {
            // 这里的 vis 就是刚刚防止一个点扩散多次的体现
            if(!vis[j] && mi > dis[j]) id = j, mi = dis[j];
        }
        vis[id] = 1;
        for(int j = G.head(id); j; j = G.nt(j)) {
            int v = G.to(j), w = G.wt(j);
            if(dis[v] > dis[id] + w) dis[v] = dis[id] + w;
        }
    }
}

显而易见的，就和当时的 Prim 算法一样，我们显然不需要用这么繁杂的方式去得到最小值，这也就意味着，Dijkstra 算法有着各种各样的优化，比如说线段树，二叉堆，斐波那契堆等等等等，其中斐波那契堆的复杂度最低 $O(n\log(n+m))$ ，但是因为代码复杂，没有太大的性价比，所以说我们一般来讲都用优先队列优化，也就是 STL 中的 $\tt priority_queue$ 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
typedef pair<ll, int > pii;
void Dijkstra(int u) {
    for(int i = 1; i <= n; i++) dis[i] = INF;
    dis[u] = 0;	
    priority_queue<pii, vector<pii >, geather<pii > >q;
    // 这里用的是小根堆，也就是求最小值，当然如果用的是大根堆，我们求的值就会变成最长路
    q.push(make_pair(0, u));
    while(!q.empty()) {
        int u = q.top().second; q.pop();
        // 这里就说明了为什么一开始不能标记初始点
        // 标记了之后我们就直接退出了……
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = G.head(u); i; i = G.nt(i)) {
            int v = G.to(i), w = G.wt(i);
            if(dis[v] > dis[u] + w) {
                dis[v] = dis[u] + w;
                q.push(make_pair(dis[v], v));
            }
        }	
    }
}

这个的复杂度比较难评，因为这个代码的一些性质，你会发现已经扩散的点，其实是有可能二次被插入到这里的，但是插入后他不会修改，而是当被访问的时候发现已经扩散就弹出去了。也就是说，我们的优先队列中元素的数量是 $m$ 量级的。所以说，复杂度就是 $O(m\log m)$ 其中 $m$ 是边的数量。

这时候，我们就发现，Dijkstra 算法的复杂度，其实也不低，当这张图是稠密图的时候，也就是说 $m≈ n^2$ 的时候，复杂度也会变得不靠谱，甚至不如 Floyd 。所以说，当图越来越稠密，暴力的复杂度性价比会越来越高。这是图论题的特有神奇现象，最小生成树的时候也有。

例三：迄今为止所有收藏

接下来就是一个颇具传奇色彩的最短路算法 —— Bellman-Ford 算法。这个算法可能大多数人没听说过，但他有着多如繁星般的优化方式，而且他的优化方式都有不同级别的挂，著名的 SPFA 算法，就是由他优化而来。

关于SPFA，他死了 —— 典故重现

其实 Bellman-Ford 算法，既可以说是 Dijkstra 算法的基础，也可以说是 Dijkstra 算法的升级。他的基础之处，在于它的松弛操作，可以说是 Dijkstra 朴素版本的基础；他的升级之处，在于可以知道是否在原图中存在负环，也可以计算有负边权的图。

首先，它的原理比较暴力，就是一直对于图上的边经行松弛操作，直到不可以松弛为止。我们知道最短路的点是不可重复的，也就是说最短路不可以成环，也就是说全图的松弛操作只会有 $n-1$ 次，综合复杂度就是 $O(nm)$ 。

而我们说他可以计算出负环，是因为负环一直满足递减的要求，也就是说，他会一直转圈，我们只需要判断 $n-1$ 次松弛完事后，再次松弛会不会有数值变化即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
struct Edge {
  int u, v, w;
};

vector<Edge> edge;

int dis[MAXN], u, v, w;
constexpr int INF = 0x3f3f3f3f;

bool bellmanford(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  dis[s] = 0;
  bool flag = false;  // 判断一轮循环过程中是否发生松弛操作
  for (int i = 1; i <= n; i++) {
    flag = false;
    for (int j = 0; j < edge.size(); j++) {
      u = edge[j].u, v = edge[j].v, w = edge[j].w;
      if (dis[u] == INF) continue;
      // 无穷大与常数加减仍然为无穷大
      // 因此最短路长度为 INF 的点引出的边不可能发生松弛操作
      if (dis[v] > dis[u] + w) {
        dis[v] = dis[u] + w;
        flag = true;
      }
    }
    // 没有可以松弛的边时就停止算法
    if (!flag) {
      break;
    }
  }
  // 第 n 轮循环仍然可以松弛时说明 s 点可以抵达一个负环
  return flag;
}

代码来自 OI-wiki 。

算法实战：这一次我一定要赢

查看相关算法标签喵！