【算法介绍】后缀数组

算法简介：高门的谒礼

这个后缀数组，还真是个玄学玩意，模板题就是紫题啊，研究起来有点难度，这篇文章就是来讲后缀数组的。所谓后缀数组，其实就是一个字符串算法，而且极为抽象。

后缀数组的主要内容，就是把一个字符串的所有后缀给排好序标上号。但是它有一些奇怪应用，更是难上加难，但是理解了以后就很简单了，这篇文章的目的就是带大家看看后缀数组的全部过程。

算法推导：御驿的径迹

那么我们刚刚就说过后缀数组的主要内容，就是把一个字符串的所有后缀排好序以后标号。那么首先我们就要知道，后缀是什么？我们首先给出后缀的一些定义。

后缀：
　　在一个字符串中对于任意的 $i\quad (1\le i\le n)$ ，后缀就是这个字符串的第 $i$ 个字符到最后一个字符的连续子串。注意注意，我们整篇文章字符串都是从 $1$ 开始的下标。

然后呢说，我们这里排序是根据字典序来排序的，所谓字典序，就是字面意思的字典顺序。两个字符串逐个字符比较，遇到第一个不一样的时候看两个字符谁的 ASCII 值小，小的那个更小。如果发现有一个字符串比对完了都没有分出大小（也就是一个字符串是另外一个字符串的前缀）那么短的那个小。

基本思路：旋规设矩

那么自古以来，我们最不缺的就是模拟了，几乎所有的算法都可以从模拟出发。同样的我们来看看最最暴力的做法会是什么样。

那么既然我们要求出所有后缀的大小，第一步肯定是要搞定后缀，由于暴力只是提供思路，所以说我们也是直接先用 string 顶替一下，方便实现。

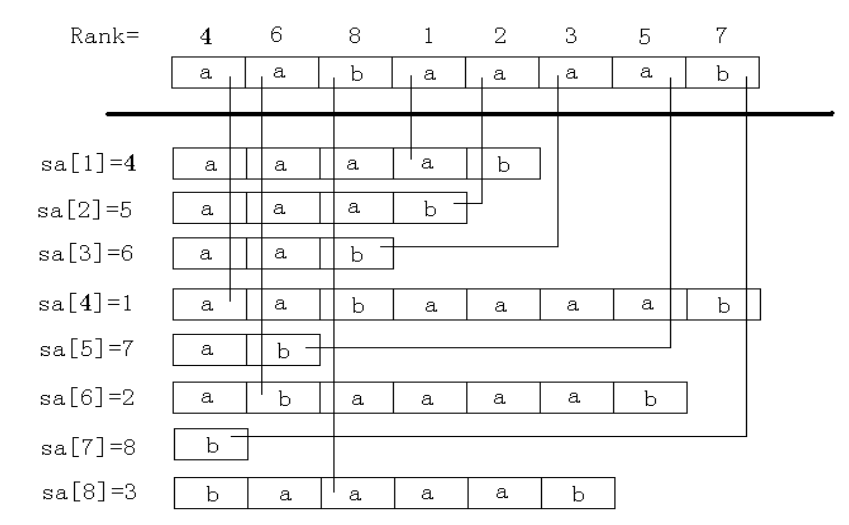
我们要求出所有字符串后缀对应的排位，我们不妨定义 $sa[i]$ 表示排序后排位为 $i$ 的字符串起点在位置 $sa[i]$ 。单从图示的角度来讲，后缀数组应该是长这样的：

vector<pair<string , int > >v;
for(int i = 0; s[i]; i++) {
    v.push_back(make_pair(s.substr(i), i));
}

这样就是属于直接搞定了所有的后缀，我的第二维还有一个整型变量，它的作用在于标记这个子串的位置。然后呢我们就可以排序 + 处理了。

sort(v.begin(), v.end());
for(int i = 0; i < v.size(); i++) {
    sa[i + 1] = v[i].second + 1;
}

然后我们也是正常的进行一波复杂度分析，一眼看上去似乎是 $O(n\log n)$ ；但是实际上，我们都应该知道的常识是 string 的 substr() 函数的复杂度应该是 $O(n)$ 的，然后字符串比较的复杂度最坏情况也应该是 $O(n)$ ，所以说真实的复杂度应该是 $O(n^2\log n)$ 。

进步思考：画则巧施

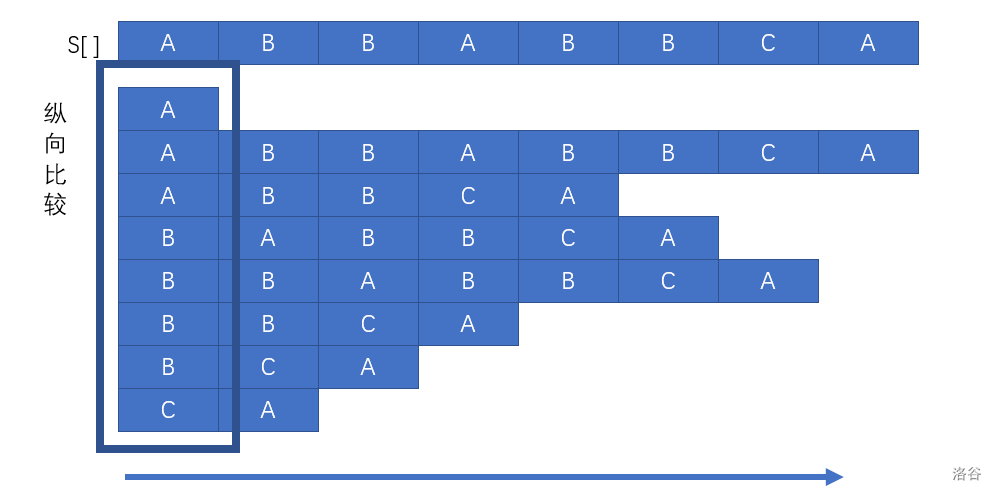
这个暴力给了我们什么提示呢？显而易见的我们不可能一次性求出所有的后缀，这样就会导致我们对于若干个字符串每两个之间的横向比较，这样就产生了 $O(n)$ 的比较复杂度。这是不优的，显然在这种情况下我们要更换思路，转战纵向比较才可以找到突破。

那么所谓纵向是怎么个说法呢？首先最最直观的就是一次性比对所有的字符串，大概可以认为是下面这样。

我们一开始时候的比较方式，就是这样的模拟形式，但是把所有的字符串都扫了一遍。这样就会出现大量的浪费，而算法的优化何来？不就是减少浪费嘛。可是说我们不是摈弃了这种做法吗？所以说这次的比较不能是线性扫描的了。而非线性做法，最不难想到的就是 $O(n \log n)$ ，从盲猜的角度来讲，一开始的复杂度是 $O(n^2\log n)$ 那么这一步优化掉一个 $O(n)$ 似乎是理所应当的。

这时候我们需要开辟新思路。

我们注意到刚刚说的一个字符串比对时的细节：

字典序顺序：
　　两个字符串逐个字符比较，遇到第一个不一样的时候看两个字符谁的 ASCII 值小，小的那个更小。如果发现有一个字符串比对完了都没有分出大小（也就是一个字符串是另外一个字符串的前缀）那么短的那个小。

直接看可能没什么感觉，但是我们来专业抓终点，“如果发现有一个字符串比对完了都没有分出大小” ，这似乎透露着不一样的味道，我们是不是可以认为，这个一个字符串比对完的时候，也就是字符串的最后一个字符的后一个，是传说中的 \0 也就是 ASCII 值最小的字符。这个就是我们学字符串时候老师说过的一个标识符。

那么，我们就来想想，如果我们把比对的字符串全都用 \0 补齐，是不是也能得到相同的效果？就是下面这样：

abaaba
aba000

还是一样的，比对到第四个的时候，发现 \0 小于 a ，于是就可以判断出下面的字符串要小于上面的那个。似乎和一开始的思路一点变化都没有？不，这只是一个契机。

这时候，我们就发现了特性，似乎字符串长度对于我们已经不再重要了，也就是说即使长度超出的极大，我们也可以通过补齐 \0 的形式来得到长度一样的串，而且这对答案没有丝毫的影响。

我觉得已经不用再提示了，直接拍板！看看上面分析的关键字：

1. 纵向比对
2. 非线性
3. 长度无关

还没反应过来的出门右转倍增算法谢谢！我们可以先猜猜看这是倍增算法，然后验证嘛，在算法的建立之初就是通过分析来在那么多优化方式中寻找一个可能性最大的，然后一个一个试过去找到答案，很少有人一步到位的。

然后接下来就是验证刚刚的猜测了，到底能不能用倍增，或者说倍增的正确性何在。首先我们明确一个终点，倍增算法的要求：处理的数据满足结合律。那么我们处理的字符串排位是否满足结合律呢？

我们姑且用 $\operatorname{substr}(i, k)$ 表示字符串 $s$ 从 $i$ 到 $i + 2^k - 1$ 的子串，如果有超出 $n$ 的部分，用 \0 补齐。那么，任意的一个后缀都可以通过若干次倍增组合而成，举个例子：

sample(01) - i = 1
 s :  a a b a a a a b
k=0:  a a b a a a a b
k=1:  a_a b a a a a b
k=2:  a_a_b_a a a a b
k=3:  a_a_b_a_a_a_a_b

下划线连接的表示一个分组，但是说由于这种静态字符画的限制，没能展现出其他的分组，所以说我还可以再来一个演示一下。

sample(02) - i = 3
 s :  a a b a a a a b
k=0:  a a b a a a a b
k=1:  a a b_a a a a b
k=2:  a a b_a_a_a a b
k=3:  a a b_a_a_a_a_b_0

我们最后的一部分超出了，但是这样的话才能保证这个字符串包括了最后一个字符，也就是他是一个后缀，最后在贴上一张经典的图片自己来体会一下关于 满足结合律 方面的正确性。

那么除了刚刚说的，字符串拼接满足结合律，还有一个重要的点，就是如何在过程中计算答案。首先我们提出一个重要的概念，就是上图中的 rank 数组。这个 rank 是干什么的呢？就是一个重要的辅助计算答案数组，其含义是 rank[i] 表示以 $i$ 为起点的后缀排序后在 rank[i] 位，详细的去看上面的内容 基本思路：旋规设矩 。

有了这个东西，他会有什么具体作用吗？这时候就要搬出结合律了，由于我们把字符串倍长了，也就是说他会由两个部分组成，而这两个部分的优先级分别是前半段大于后半段，因为如果前半段就已经分出大小，那么后半段就没有必要计算了。

那么前后半段的大小，都分别是什么呢？显然的是我们已经求出来的 rank 也就是说我们每一次更新出来的 rank 数组，都是辅助计算下一层答案用的，这就是这个算法非常巧妙的一点了。

那么其实这里就是利用每次的 rank 来搞出上图中的 x y 也就是两个关键字，然后排序就可以了。但是这样倍增要倍增到什么时候呢？显而易见的是如果 $2^k \ge n$ 我们就可以停下来了。因为 $2^k = n$ 的时候，我们也就只是刚刚把 $1$ 开头的后缀完整算出来，其他的就都已经溢出用 $0$ 补齐了；那 $2^k > n$ 就更加不用说。

说了这么多，我们先来尝试写一下这次的代码吧，应该不算特别难写。

int SA[N], RK[N << 1];
int rk[N << 1]; 
// 翻倍的原因是倍增的时候我们会访问到 rk[i + k]

inline void Work() {
    n = strlen(s + 1);
    for(int i = 1; i <= n; i++) {
        SA[i] = i; RK[i] = s[i];
        // 这里的 SA 就是一个编
        // 因为最终都会溢出成后缀，所以说 SA 会慢慢被改正成正确答案
        // RK 的初始值用 ASCII 是因为 字典序排序天生用的 ASCII
    }
    for(int k = 1; k < n; k <<= 1) {
        // 正经的双关键字排序
        sort(SA + 1, SA + n + 1, [&](int a, int b) {
            return RK[a] == RK[b] ? RK[a + k] < RK[b + k] : RK[a] < RK[b];
        });
        // 交换 RK 和 rk ，因为一会重新标号要用 RK 存储
        // 但是直接覆盖会丢失数据，所以备份
        swap(RK, rk); int cnt = 0; // cnt 是新的标号
        for(int i = 1; i <= n; i++) {
            // 和上一个一样，就还是 cnt
            if( rk[SA[i]] == rk[SA[i - 1]] && 
                rk[SA[i] + k] == rk[SA[i - 1] + k]) {
                    RK[SA[i]] = cnt;
            }
            else {
                // 不然的话就更大（因为已经排好序）
                RK[SA[i]] = ++cnt;
            }
        }
    }
    // 上面的循环中 k = 2^x < n, 如果跳出来了就说明 2^x >= n 说明都溢出成后缀了，答案也变得可用
    for(int i = 1; i <= n; i++) {
        printf("%d ", SA[i]);
    }
}

那么又到了万众瞩目的分析复杂度时间，首先我们外层的倍增一眼 $O(\log n)$，内部由于那个不争气的 sort 导致了内部的复杂度是 $O(n\log n)$，那么总体复杂度就是 $O(n\log^2 n)$ 。

最终优化：繁绘隅穹

上面说的思路似乎是极限了，貌似无懈可击是不是？我们也分析了，上面的复杂度瓶颈在于 sort ，我们只有两个关键字，但是却需要用到 $O(n\log n)$ 复杂度的 sort ，非常难受。也就是说，接下来的突破方式，就是在排序上了。

可是我们目前所熟知的排序，要么是复杂度低劣，像冒泡插入等；要么是上限低，快排归并上限就是 $O(n\log n)$ 不能再快了。那么难道就是止步于此了吗？

我相信大家在普及组初赛知识的时候都学过一个重要的排序算法，基数排序。这个排序方式和希尔排序一样，都是学初赛时老师提到的小概念，就是不会写，但要知道大概的意思。希尔排序我们可以直接排除，大大滴不稳定，最坏情况竟然可以直接飙到 $O(n^2)$ 这是在想屁吃呢？所以说只能慢慢的把目光投向基数排序。

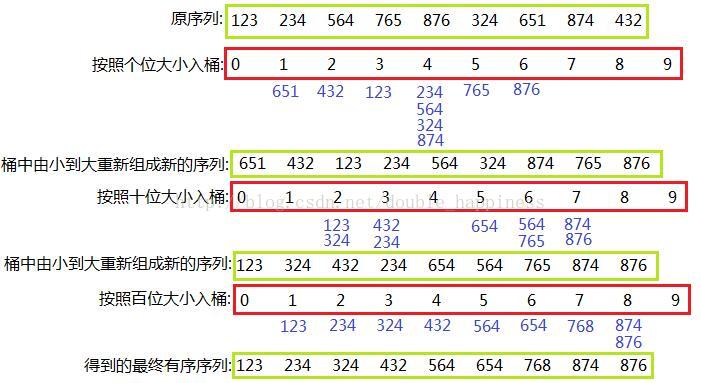
基数排序是什么呢？大概讲一下基础概念。最基础的，如果是对一堆十进制数排序的话，那么我们直接开十个桶，把个位依次存进去。然后按照桶里的顺序把它取出来，这样的话个位就是有序的了；然后对于十位做同样的操作即可，循环往复，知道不存在更高位。

然后我们就发现了，这样的排序算法复杂度非常非常非常低。单从这个十位数排序来讲，它的复杂度就是 $O(n\log_{10} n)$ 也就是位数乘以长度。

那么这个思想能运用到我们这里的排序吗？显然可以，我们可以把这个二元组看作是一个 $n$ 进制数，这样的话我们就可以在 $\Theta(2n)$ 的复杂度搞定排序。

我们一样的也是开一个桶，不过这个桶的大小应该是 $n$ 也就是字符串的后缀的数量。然后一开始的时候，我们排序是只有单个的字母，所以说我们可以写出这样的代码：

for(int i = 1; i <= n; i++) buc[s[i]]++; // buc 是我们说的桶
int m = 127; // 值域，目前是整体的 ASCII 
// 前缀和的目的是找到有多少比自己小的字符串以知道排名
for(int i = 0; i <= m; i++) buc[i] += bus[i - 1];
for(int i = n; i >= 1; i--) SA[buc[s[i]]--] = i; // SA[排名]=id
// 字面意思的计算 rank
for(int i = 1; i <= n; i++) RK[SA[i]] = RK[SA[i - 1]] + (s[SA[i]] != s[SA[i - 1]]);

准备就绪后，我们需要正式的开始处理内部的数据了。那么先根据刚刚的思路，优先基数排序第二关键字，然后排第一关键字，这样就可以保证是以一关键字优先的排序了。

for (w = 1; w < n; w <<= 1, m = n) {
    // 对第二关键字：id[i] + w进行计数排序
    memset(buc, 0, sizeof(buc));
    // 备份大 SA 到小 sa，防止覆盖丢失数据
    memcpy(sa + 1, SA + 1, n * sizeof(int));
    for (i = 1; i <= n; ++i) ++buc[RK[sa[i] + w]];
    for (i = 1; i <= m; ++i) buc[i] += buc[i - 1];
    for (i = n; i >= 1; --i) SA[buc[RK[sa[i] + w]]--] = sa[i];

    // 对第一关键字：id[i]进行计数排序
    memset(buc, 0, sizeof(buc));
    memcpy(sa + 1, SA + 1, n * sizeof(int));
    for (i = 1; i <= n; ++i) ++buc[RK[sa[i]]];
    for (i = 1; i <= m; ++i) buc[i] += buc[i - 1];
    for (i = n; i >= 1; --i) SA[buc[RK[sa[i]]]--] = sa[i];
	
    // 和 sort 那会一样
    memcpy(rk + 1, RK + 1, n * sizeof(int));
    for (p = 0, i = 1; i <= n; ++i) {
        if (rk[SA[i]] == rk[SA[i - 1]] &&
            rk[SA[i] + w] == rk[SA[i - 1] + w]) {
            RK[SA[i]] = p;
        }
        else {
            RK[SA[i]] = ++p;
        }
    }
}

这样就可以处理好我们的最终答案，大 O 复杂度应该是 $O(n\log n)$，似乎很对啊。但是你仔细看看，你细品细细的品，发现了什么，常数奇大无比。这个 $\log $ 的循环里，放了 $12$ 个复杂度在 $O(n)$ 左右的循环和清空，非常的不划算，我们线段树仅仅是 $4$ 的常数我们都嫌大，更别说这里直接翻了三倍！过于不划算了。

也就是说我们要对于这里的内容经行优化。我们发现了，这里的问题就在于两次的基数排序。那么想要加强它，就说明了有一个基数排序是不必要的。动用你强力的第六感想想，应该是第二关键字的排序，首先这玩意我们一开始就说了，我们倍增过去，第二关键字有大部分为空。也就是说不同的空白部分组成了第二关键字的排序，我们大可以直接根据空白部分处理掉他们，这样就可以省掉一大堆的常数。

然后我们就可以得到一个更加玄学的代码：

void suffix_array() {
    // Step 1: 初始化阶段，基于单个字符排序
    // 统计每个字符的频率
    for(int i = 1; i <= n; i++) buc[s[i]]++;
    // 计算前缀和，确定每个字符在后缀数组中的区间
    for(int i = 'a'; i <= 'z'; i++) buc[i] += buc[i - 1];
    // 从后往前填入后缀数组，确保排序的稳定性
    for(int i = n; i >= 1; i--) sa[buc[s[i]]--] = i;
    // 根据排序结果初始化排名数组，初始排名由字符值决定
    for(int i = 1; i <= n; i++) 
        rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]);
    // Step 2: 倍增阶段，每次排序按 2k 的长度划分两个部分
    for(int k = 1; k <= n; k <<= 1) {
        // 计数排序的第一部分：基于后半部分 (rk[sa[i] - k]) 排序
        // 由于 rk 是连续的排名数组，buc 只需用作计数，不需要前缀和
        for(int i = 1; i <= n; i++) buc[rk[sa[i]]] = i;
        for(int i = n; i >= 1; i--) 
            if(sa[i] > k) SA[buc[rk[sa[i] - k]]--] = sa[i] - k;
        // 特殊处理：对于超出范围的后缀，直接将其放入排序结果中
        for(int i = n - k + 1; i <= n; i++) SA[buc[rk[i]]--] = i;
        // 更新排名数组：根据当前后缀的两部分排名 (rk 和 rk + k) 确定新排名
        for(int i = 1; i <= n; i++) 
            RK[SA[i]] = RK[SA[i - 1]] + 
                !(rk[SA[i]] == rk[SA[i - 1]] && rk[SA[i] + k] == rk[SA[i - 1] + k]);
        // 将 SA 和 RK 的结果更新到 sa 和 rk 中，为下一轮倍增做准备
        swap(rk, RK); swap(sa, SA);

        // 如果所有后缀的排名都已唯一 (rk[sa[n]] >= n)，可以提前结束
        if(rk[sa[n]] >= n) break;
    }
}

这样的话，我们的常数大大降低，缩小到了原来的三倍左右，是个不错的优化，这也是目前的最终版本了。后缀数组还有一个 $O(n)$ 的版本（我当然是不会啦 qwq ）

算法模板：金塔的香献

那么趁热打铁，来看看这种算法如何应用。

题目大意

读入一个长度为 $n$ 的由大小写英文字母或数字组成的字符串，请把这个字符串的所有非空后缀按字典序从小到大排序，然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 $1$ 到 $n$ 。

题目思路

好吧绝对不是我没找到一个合适的题，，，，

就当是练手了。这个就是最基础的后缀数组，我重新申明一下 SA 和 RK 的定义。

• SA ：排名为 $i$ 的字符串
• RK ：字符串 $i$ 的排名

别忘了，很重要

题目代码

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

const int N = 1e6 + 10;

char s[N];

inline void Input() {
    scanf("%s", s + 1);
}

int n;

int SA[N], sa[N];
int RK[N << 1], rk[N << 1];
int buc[N];

inline void SuffixArray() {
    for(int i = 1; i <= n; i++) buc[s[i]]++;
    for(int i = 0; i < 128; i++) buc[i] += buc[i - 1];
    for(int i = n; i >= 1; i--) SA[buc[s[i]]--] = i;
    for(int i = 1; i <= n; i++) RK[SA[i]] = RK[SA[i - 1]] + (s[SA[i]] != s[SA[i - 1]]);
    for(int k = 1; k <= n; k <<= 1) {
        for(int i = 1; i <= n; i++) buc[RK[SA[i]]] = i;
        for(int i = n; i >= 1; i--) if(SA[i] > k)
            sa[buc[RK[SA[i] - k]]--] = SA[i] - k;
        for(int i = n - k + 1; i <= n; i++) sa[buc[RK[i]]--] = i;
        for(int i = 1; i <= n; i++) 
            rk[sa[i]] = rk[sa[i - 1]] + 
                !(RK[sa[i]] == RK[sa[i - 1]] && RK[sa[i] + k] == RK[sa[i - 1] + k]);
        swap(rk, RK); swap(sa, SA);
        if(rk[sa[n]] >= n) break;
    }
}

inline void Work() {
    n = strlen(s + 1);
    SuffixArray();
    for(int i = 1; i <= n; i++) {
        printf("%d ", sa[i]);
    }
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

算法拓展：百柱的酣宴

接下来是这个算法的主要应用。后缀数组的主要用法是求后缀最长公共前缀，看上去好神奇啊，明明是后缀算法，最后主要应用是求最长前缀？！

模型构建：营造者的担当

如果我们设 height[i] 表示排名为 $i$ 和 $i - 1$ 的后缀的最长公共前缀。那么就可以得到一个显而易见的式子：$height[i]=\operatorname{LCP}(sa[i], sa[i - 1])$ 。

但是这个式子对于我们似乎用处不大，如果是让我们暴力求公共前缀还是算了，显而易见这是超时的。我们先给结论，就是 $height[rk[i]]\ge height[rk[i - 1]]-1$ 。证明的话，我们可以来一个小小的分类讨论：

• 当 $height[rk[i-1]]\le1$ 时，上式显然成立
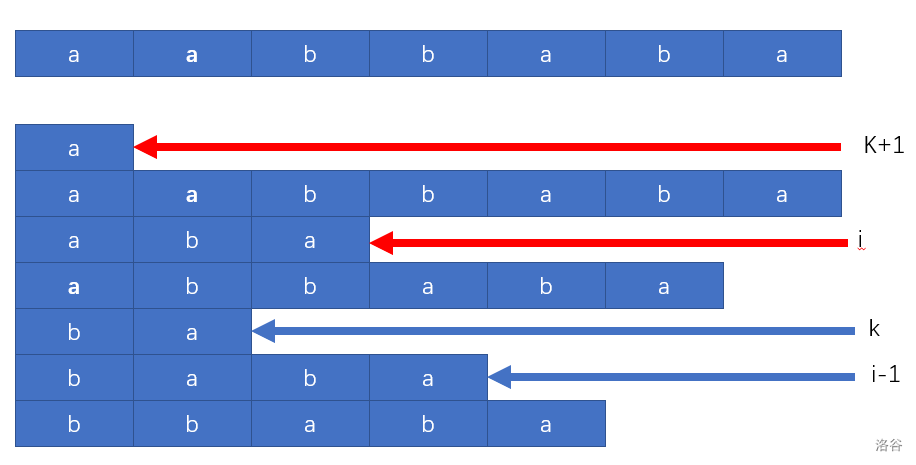
• 当 $height[rk[i-1]] > 1$ 时：

我们在后缀数组找找一个后缀，设它的起点是 $i - 1$ 。排名比它靠前的一个，我们把它的起点称为 $k$ 。然后分别删去他们的首字母，就会得到上图中红色的 $i-1 \rightarrow i$ 和 $k\rightarrow k+1$，这当然不是巧合，自己用后缀的定义推一推就知道了。

然后就有一个不那么明显的细节，就是他们的相对大小没有变，也就是说一开始 $sa[k]\lt sa[i-1]$ 然后删除了首字母以后就是 $sa[k+1]\lt sa[i]$ 这是为什么？不难发现他们的首字母相同，因为在字典序比较时，第一个不相同的才会影响结果，但是首字母相同那么就说明他是无关紧要的，所以删去了以后顺序没有变。

那么这有什么特殊的吗？显然有。这就是我们苦苦寻找的公共前缀啊，这个两个字符串首字母一样，那么它的公共前缀一定的首字母一定是这个字母，他们的公共前缀长度就从 $height[rk[i-1]]\ $变成了 $height[rk[i-1]-1]$ 。

然后说，我们继续来推。首先大家知道一个常识，$\operatorname{LCP}(i,k)=\min(\operatorname{LCP}(i,j),\operatorname{LCP}(j,k))$ 就是说我们这个 SA 都是已经排好序了，这种时候相邻的部分一定是公共部分较多的，不然他也不会这么排，字典序排序导致了从第一个 SA 开始到最后一个，单论第一个字符，他一定是按照顺序排列的，如果两个排好序的 $i,k$ 他们有公共前缀，他们中间的任意一个两两配对都应该至少是 $\operatorname{LCP}(i,k)$ 的长度，也就是 $\operatorname{LCP}(i,k)=\min\limits_{1\le i\le j\le k\le n}\{\operatorname{LCP(j,j+1)}\}$ 。

我们可以试想一下，对于比第 $i$ 个字符串的排名更靠前的那些字符串，谁和第 $i$ 个字符串的相似度最高（这里说的相似度是指最长公共前缀的长度）？显然是排名紧邻第 $i$ 个字符串的字符串，即 $sa[rk[i]-1]$ 。但是我们前面求得，有一个排在 $i$ 前面的字符串 $k+1$，$\operatorname{LCP}(rk[i],rk[k+1])=height[rk[i-1]]-1$，又因为$height[rk[i]]=\operatorname{LCP}(i,i-1)\ge \operatorname{LCP}(i,k+1)$。所以 $height[rk[i]]\ge height[rk[i-1]]-1$，至此证毕。

算法模板：工艺家的奇想

有了上面的强劲性质，我们就可以用一种近乎暴力的方式计算出 height 数组：

inline void HeightArray() {
    for(int i = 1, k = 0; i <= n; i++) {
        while(s[i + k] == s[sa[rk[i] - 1] + k]) k++;
        H[rk[i]] = k;
        if(k) k--;
    }
}

算法例题：圣古的库藏

老规矩，来到简单模板题看看。

题目大意

给你一个长为 $n$ 的字符串，求不同的子串的个数。

我们定义两个子串不同，当且仅当有这两个子串长度不一样或者长度一样且有任意一位不一样。

子串的定义：原字符串中连续的一段字符组成的字符串。

题目思路

好把这个还真的挺玄学，我们学的 SA 一直都是求公共公共公共……哎？我们求总方案数然后挖掉公共部分不就好了，然后这道题就非常愉快的通过了！

题目代码

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

const int N = 1e5 + 10;

int n;
char s[N];

inline void Input() {
    read(n);
    scanf("%s", s + 1);
}

int sa[N], SA[N], rk[N << 1], RK[N << 1];
int buc[N];

void SuffixArray() {
    for(int i = 1; i <= n; i++) buc[s[i]]++;
    for(int i = 1; i <= 127; i++) buc[i] += buc[i - 1];
    for(int i = n; i >= 1; i--) sa[buc[s[i]]--] = i;
    for(int i = 1; i <= n; i++) 
        rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]);
    for(int k = 1; k <= n; k <<= 1) {
        for(int i = 1; i <= n; i++) buc[rk[sa[i]]] = i;
        for(int i = n; i >= 1; i--) 
            if(sa[i] > k) SA[buc[rk[sa[i] - k]]--] = sa[i] - k;
        for(int i = n - k + 1; i <= n; i++) SA[buc[rk[i]]--] = i;
        for(int i = 1; i <= n; i++) 
            RK[SA[i]] = RK[SA[i - 1]] + 
                !(rk[SA[i]] == rk[SA[i - 1]] && rk[SA[i] + k] == rk[SA[i - 1] + k]);
        swap(rk, RK); swap(sa, SA);
        if(rk[sa[n]] >= n) break;
    }
}

int H[N];

inline void HeightArray() {
    for(int i = 1, k = 0; i <= n; i++) {
        while(s[i + k] == s[sa[rk[i] - 1] + k]) k++;
        H[rk[i]] = k;
        if(k) k--;
    }
}

inline void Work() {
    SuffixArray();
    HeightArray();
    ll ans = 1LL * n * (n + 1) / 2;
    for(int i = 2; i <= n; i++) {
        ans -= H[i];
    }
    printf("%lld\n", ans);
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

算法实战：天园的理想

查看相关算法标签喵！

参考资料（以下排名不分先后）

• 浅谈后缀数组算法 - 洛谷专栏
• 后缀数组简介 - OI Wiki
• 五分钟搞懂后缀数组！后缀数组解析以及应用(附详解代码)_后缀数组模板-CSDN博客
• 基数排序详解-CSDN博客
• 最详细的【基数排序】—-排序算法，思路清晰动图保姆级讲解，五分钟搞懂！_csdn基数排序动图-CSDN博客
• 后缀数组 学习笔记 - xMinh讲解.html)