算法简介：晨曦酒庄的大公子

轮廓线 DP 作为状压 DP 的一大变种，难度极高，模板即是紫题，这里浅浅的讲一讲。

算法演示：清算黑暗的炎之剑

例题选讲：钢铁炽焰

用宽为 $2$ 高为 $1$ 的砖头去平铺一个宽为 $w$ ，高为 $h$ 的矩形，问有多少种不同的方案。

如下图所示，平铺 $4\times2$ 的有 $5$ 种方案， $3\times2$ 有 $3$ 种方案。

方案数

例题思路：流火焦灼

这就是一道轮廓线 $\tt DP$ 的模板题，我们设一个轮廓的状态为这一行的某一个点有或没有填充，用二进制表示。

那么首先可以列出状态：$dp[i][mask]$ 当第 $i$ 行的轮廓长这样的时候，方案的数量。

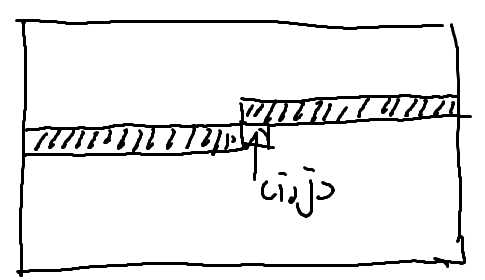
这里定义一下我们所谓的《第 $i$ 行轮廓》当我们枚举到点 $(i,j)$ 的时候，轮廓长这样：

那么递推怎么递推呢？我们只考虑当前的这一个点如何填充的话，那么不重不漏的考虑应该只需要讨论以我这个点为右下角的横竖两种摆法。那么其实转移方程也好想，我们枚举一个 $m ask$ 表示上一行的轮廓，那么如果上面那一行未被填充，这里就是竖着排，不然排不满；如果上一行的这里已经填充，那么我这个位置就可以考虑竖着或者横着，横着的前提是旁边的那个没有填充。

例题代码：炙热余烬

最后提一嘴，因为这个可能会爆空间，所以用的滚动数组。

inline void Work() {
    dp[0][(1 << n) - 1] = 1;
    int cur = 0;
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            cur ^= 1;
            for(int mask = 0; mask < (1 << n); mask++) {
                if(dp[cur ^ 1][mask] == 0) continue;
                if(!(mask & (1 << j - 1))) {
                    dp[cur][mask | (1 << j - 1)] += dp[cur ^ 1][mask];
                }
                else {
                    if(j > 1 && !(mask & (1 << j - 2))) {
                        dp[cur][mask | (1 << j - 2)] += dp[cur ^ 1][mask];
                    }
                    dp[cur][mask ^ (1 << j - 1)] += dp[cur ^ 1][mask];
                }
            }
            memset(dp[cur ^ 1], 0, sizeof(dp[cur ^ 1]));
        }
    }
    printf("%lld", dp[cur][(1 << n) - 1]);
}