题面

小A和小B又在通过游戏决一胜负了。

今天他们玩的游戏是这样的，小A拿出了张卡片，每张卡片上都写了一个数 $a$ 。他们每个人轮流交替取走一张卡片，直到取完，小A先取。

记小A取走的卡片的权值和为 $A$ ，小B取走的卡片的权值和为 $B$ ，则小A最终得分为 $|A|-|B|$ 。小A自然希望自己的得分最大，小B则希望其得分最小。

优策略的情况下，小A的最终得分是多少？

$n\le 1e5$

思路

不难发现，这就是一道非常经典的博弈类型的贪心题。这里有两个人，小A和小B，他们分别有着自己的决策 $A,B$ ，得分的表现形式为 $|A|-|B|$ ，所以说这是一道双变量的博弈。而处理这种问题的方法之一，就是把双变量转化为单变量。而想要把双变量转化为单变量，我们需要找到不变量。

观察题目，不难发现不变量就是所有元素之和。我们记 $sum = \sum\limits_{i=1}^n a_i$ 。那么当小A取得行动得分 $|A|$ 时，小B的分数自然是 $|sum-A|$ 。最后的答案就等价于 $|A|-|sum-A|$ 。如果我们用函数 $f(A)$ 表示结果，我们可以得到函数 $f(A) = |A|-|sum-A|$ 。

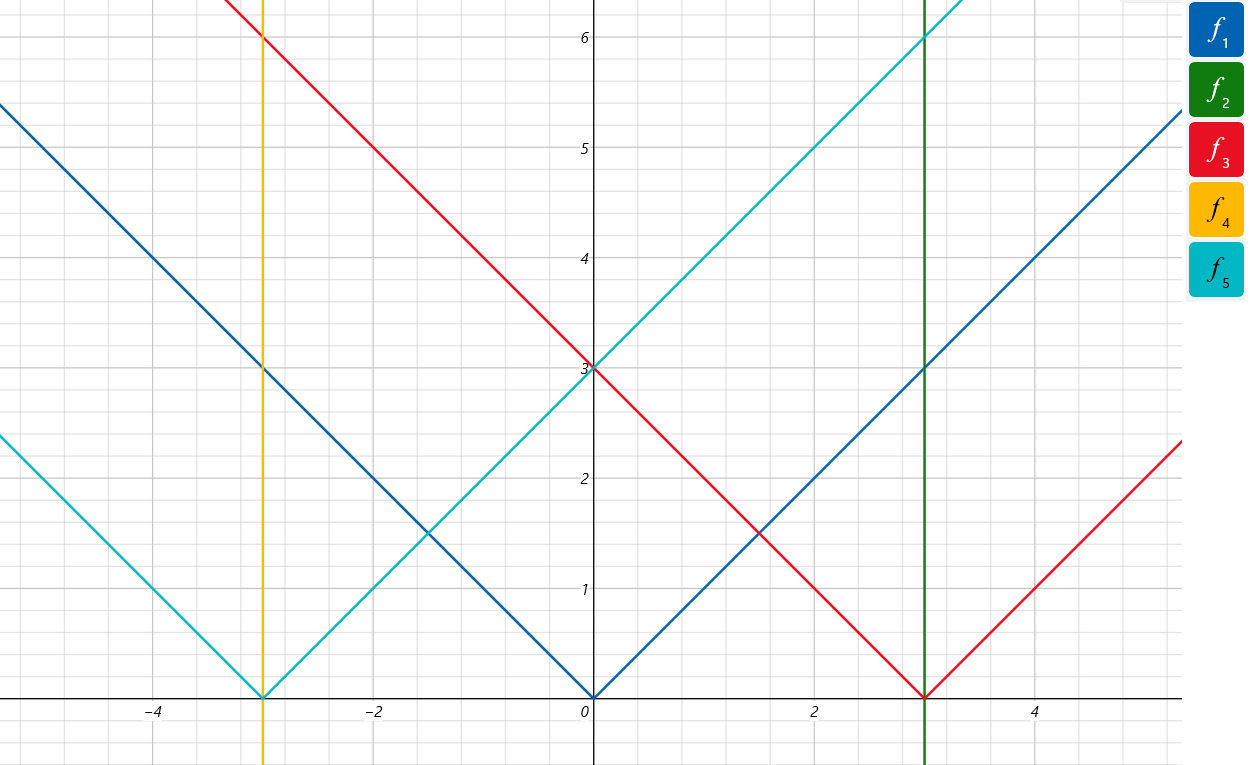
那么对于处理绝对值的问题我们可以分为 $sum>0$ 和 $sum <0$ 两种表示。首先画出函数 $f_1(y) = |x|$ 的图像。

本题需用函数

这个图中的深蓝色 $f_1$ 函数就是我们的绝对值函数，我们下面分为两种情况考虑。

  1. $sum>0$
    图中的深绿色 $f_2$ 函数表示 $sum>0$ 时的一种取值，与其对应的红色函数 $f_3(A)=|sum-A|\ \ \ (sum>0)$
  2. $sum<0$
    图中的浅黄色 $f_4$ 函数表示 $sum<0$ 时的一种取值，与其对应的青色函数 $f_5(A)=|sum-A|\ \ \ (sum<0)$

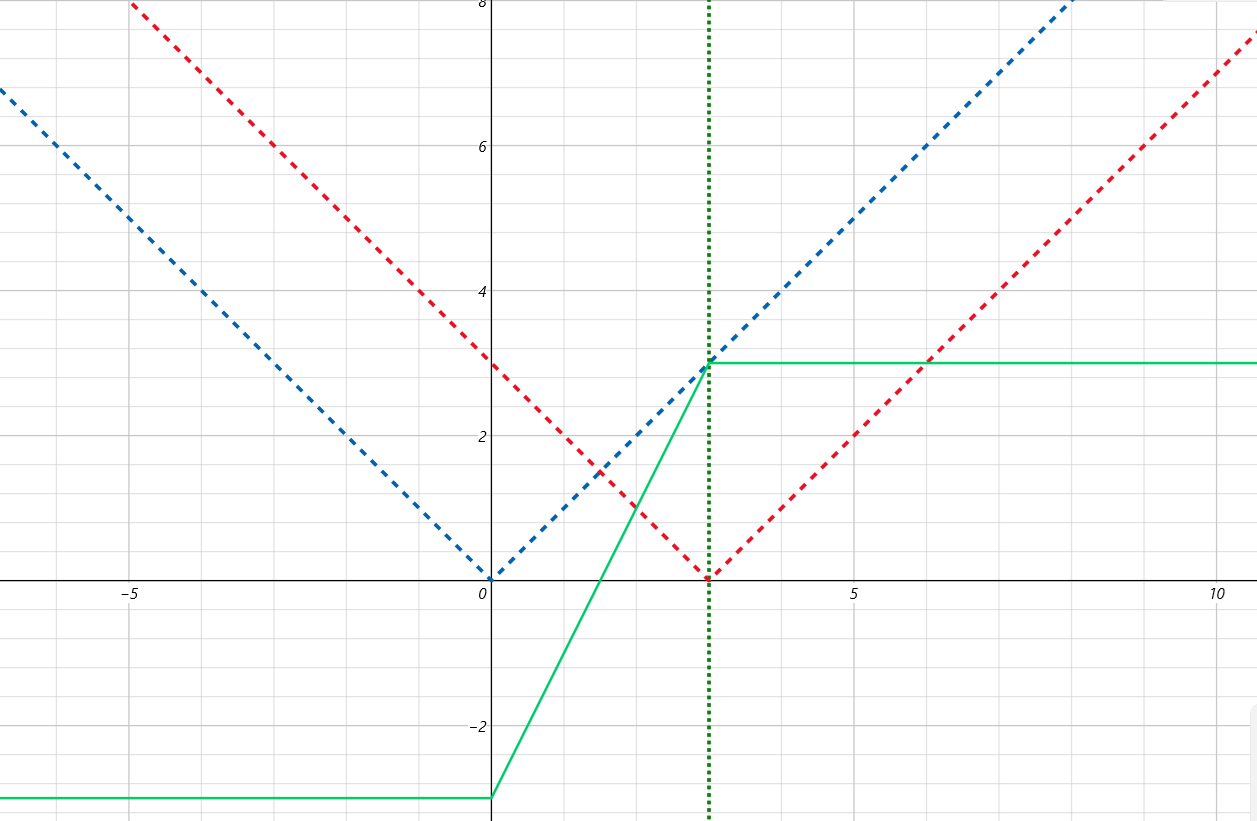
那么当两个函数相减，分别得到两种函数的时候，他们的图像长下面这样：

图中的实线函数是当 $sum > 0$ 时的一种可能的函数取法。不难发现他是呈现一个单调不降的形式，那么也就是说我们的最终答案 $f(A)=|A|-|sum-A|$ 在 $sum > 0$ 时取决于 $A$ 的大小，$A$ 越大，$f(A)$ 越大。而题目说的小A想要让自己的得分大，其实就是想要让自己取到的权值和 $A$ 尽可能大；小B想要让得分少，其实就是想要让 $A$ 小，而 $A$ 小了，那么 $B = sum-A$ 就大了。也就是说，在 $sum > 0$ 的时候，两人的都希望自己取的数尽可能大，那么其实就是数组从大到小排序 A 先手，两人轮流取。

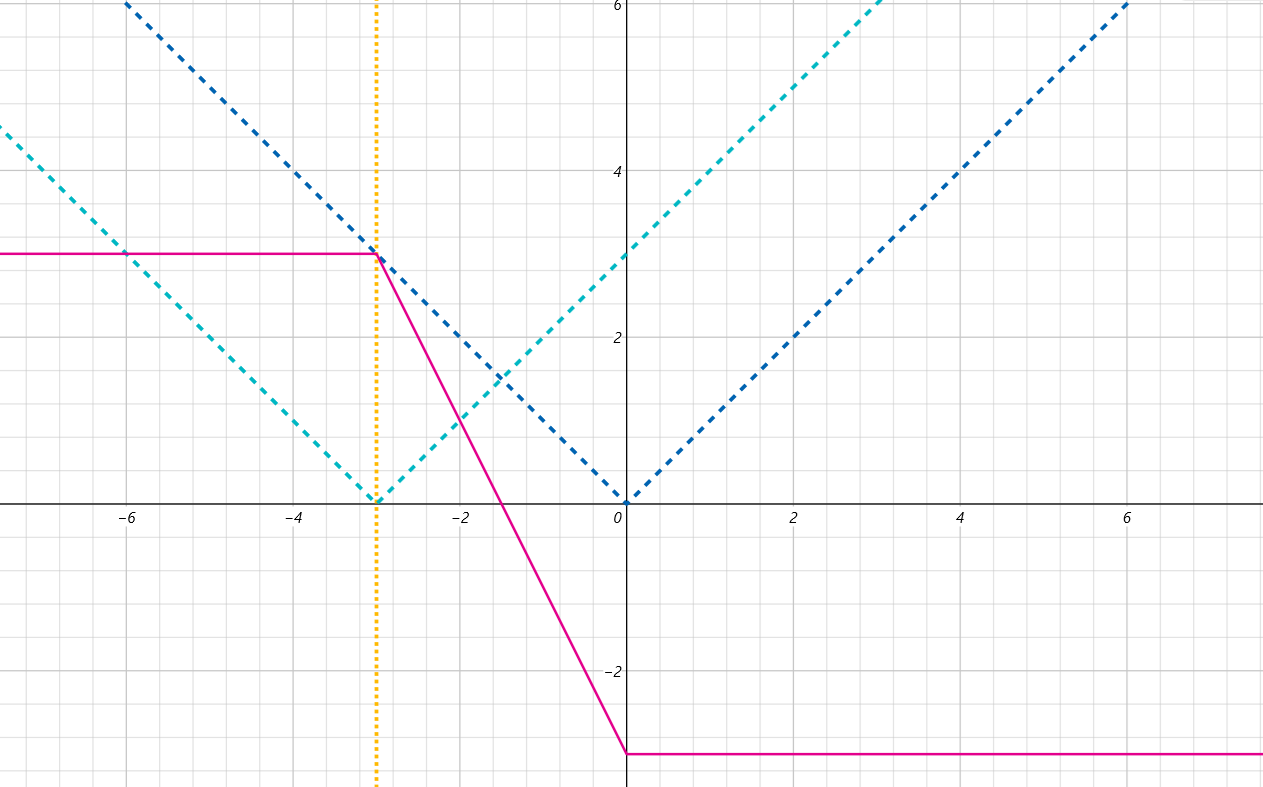
说完 $sum > 0$ 那么 $sum < 0$ 其实也是同理。我们还是先给出函数图像。

图中的实线函数是当 $sum < 0$ 时的一种可能的函数取法。不难发现他是呈现一个单调不升的形式，那么也就是说我们的最终答案 $f(A)=|A|-|sum-A|$ 在 $sum < 0$ 时取决于 $A$ 的大小，$A$ 越大，$f(A)$ 越小。而题目说的小A想要让自己的得分大，其实就是想要让自己取到的权值和 $A$ 尽可能小；小B想要让得分少，其实就是想要让 $A$ 大，而 $A$ 大了，那么 $B = sum-A$ 就小了。也就是说，在 $sum < 0$ 的时候，两人的都希望自己取的数尽可能小，那么其实就是数组从小到大排序 A 先手，两人轮流取。

那么这就是这道题的全部内容，最后的代码其实就是通过判断数组所有元素总和是正数还是负数在选择排序方式即可。

这也为我们打开了双变量博弈问题的另一种思路，数学分析。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
// #pragma GCC optimize(2)
// #pragma GCC optimize(3, "Ofast", "inline")
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

const int N = 1e5 + 10;

int n;
int a[N];

ll sum;

inline void Input() {
    read(n);
    for(int i = 1; i <= n; i++) {
        read(a[i]);
        sum += a[i];
    }
}

inline void Work() {
    sort(a + 1, a + n + 1, [](int a, int b) {
        if(sum > 0) return a > b;
        return a < b;
    });
    ll A = 0, B = 0;
    for(int i = 1; i <= n; i++) {
        if(i % 2) A += a[i];
        else B += a[i];
    }
    printf("%lld", llabs(A) - llabs(B));
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}