算法简介:释凌咏冰
这篇文章是基于 【算法介绍】连通分量 | 祝馀宫 改进总结得到的,可以先阅读上篇,然后继续阅读本篇,包括一些前置知识比如说强连通分量:【算法介绍】Tarjan 求强连通分量 | 祝馀宫 这个必须阅读,不然很难理解本篇内容(
所谓双连通分量,分为点双连通和边双连通,以及它们对应的概念割点以及割边,还有我会讲的点双连通缩点,和边双连通缩点。就难度而言,这两个其实差不太多,但是点双连通缩点的概念以及实现却略有难度。
算法演示:周天运转
边双连通分量:云尽光生
首先我们来介绍一下,边双连通分量 (e-DCC) 的概念。如果我们在一个图中,把这个图的任意一边切断,依然能保持连通,那么这个图就被称为是边双连通的;那么一个无向图中,每一个极大的边双连通的子图,我们称之为边双连通分量。

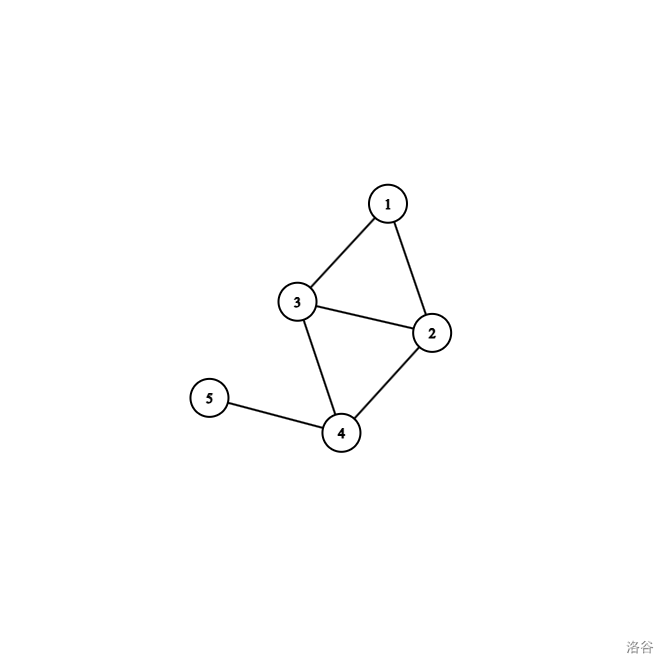
这样一看,我们可以试着找一找边双连通分量。比如说子图 $1-2-3$ 删去任意的一条边,他都保持连通,所以他是边双连通的,但是他不是极大的,显然的包含这个子图 $1-2-3$ 的还有 $1-2-3-4$ ,它就是包含他最大的边双连通的子图了,也就是说,他是这个图的边双连通分量之一。而为什么没有 $5$ ?因为 $5$ 唯一的一边指向 $4$ ,删去了就会不连通,也就是说 $5$ 自成一个边双连通分量。
有了上面的示例,我们就发现边双连通分量和强连通分量有一个极大的共性:都是环,一定要有环,才能保证破开来仍然连通,而且这个环是在无向图意义下的,也就是说,如果把它认为是两条相反的单向边,那他的环只能用一对边中的一条构成。这个是什么意思?如果你把刚刚的示例换为有向图,他的有向边是由无向边拆分出来的两条,也就是说对于边 $1-2$ 会变为 $1\rightarrow2,2\rightarrow1$ 。这样处理完之后去跑强连通分量的代码,就会导致 $5$ 也被算到了一起,这样是绝对不允许的,造成这样的原因,就是在有向图中,$4\rightarrow5,5\rightarrow4$ 被认为是一个环,然后就被算到了一起,这个是我们在写边双连通分量中要注意的一个点。
那么我们要如何记录两条边是相反的呢?因为我们每次存储无向边都是用连着的两个相反的有向边得到,这样就是没问题的。那么在我的实现过程中,边是从 $1$ 开始的,但是我们发现 1^1=0,0^1=1; 2^1=3,3^1=2 这就导致很麻烦,所以说在用 Tarjan 求边双连通分量的时候,我一般是把链式前向星变成从 2 开始计数。
用这样的建模形式,我们就发现其实边双连通分量就是无向图意义下的强连通分量,那么它的缩点以及处理过程都是好处理的。不过还有一个问题,就是栈中点还需不需要标记。显然不需要了,因为标记是否在栈中,目的是区分有向图中的四种边,但是在无向图中不会有这样的情况,这是因为在无向图中只有两种边:树边和返祖边。因为他是无向图,在搜索的过程中只要能搜的都会搜到,也是因为他是无向图,所谓前向边和返祖边其实都已经没有区别了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| void Tarjan(int u) {
dfn[u] = low[u] = ++cntd;
stk.push(u);
for(int i = G.head(u); i; i = G.nt(i)) {
int v = G.to(i);
if(vise[i^1]) continue;
vise[i] = vise[i^1] = 1;
if(!dfn[v]) {
Tarjan(v);
low[u] = min(low[u], low[v]);
}
else {
low[u] = min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]) {
++cntc;
int v = stk.top(); stk.pop();
while(v != u) {
col[v] = cntc;
clb[cntc].push_back(v);
v = stk.top(); stk.pop();
}
col[v] = cntc;
clb[cntc].push_back(v);
}
}
|
那么边双连通缩点的方式,就和这个强连通分量缩点的形式完全一样了。这里不再重复,还是那句话,如果你没有看过【算法介绍】Tarjan 求强连通分量 | 祝馀宫 就来看这篇文章,非常不建议,要是没看的还是先点出去看看强连通分量再回来。
那么说完了边双连通分量还有它的缩点,接下来是他的一大应用 —— 桥。
什么是桥?我们上面其实已经说过了,一个边双,它里面一定不存在一条边删除后会使得原图不连通,那么如果存在,这条边就是我们说的桥。也就是说,边双缩点后,每一条边都是桥,这也能看出边双缩点后的无向图会变成一棵树。
那么我们还是根据 low 和 dfn 的关系来判断什么是桥。显然的,如果某一条边是桥的话,他较深的那个端点,一定不论如何都到达不了较浅那个端点的位置及以上,也就是说,假设我们现在有一个点 $u$ ,他的儿子是 $v$ ,$v$ 以及 $v$ 的子孙所能到达的最小 dfn 值,也就是 low[v] 一定会比 dfn[u] 大。那么这个点 $u$ 指向 $v$ 的无向边就是桥,这就是桥的判定方式了。

代码很简单,就是在发现一个树边并搜索完回溯的时候,判断 $low[v]\gt dfn[u]$ 即可。代码很简单,不再赘述。
总结一下,我们可以想想边双的一些性质,用来作题:
- 桥在被割断后图会变为两段
- 边双缩点后,原图会变为一颗树
- 同一个边双连通分量内的点,一定存在环,而且是环环相扣,任意两个点之间都至少有两条完全不含重复点的路径存在(起点和终点不算)。
点双连通分量:浮云霜天
这下边双完了,我们接下来就是点双。点双的定义和边双差不多,如果我们在一个图中,把这个图的任意一点删除,依然能保持连通,那么这个图就被称为是点双连通的;那么一个无向图中,每一个极大的点双连通的子图,我们称之为点双连通分量。
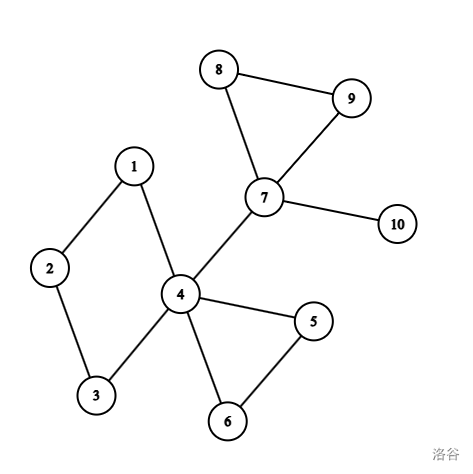
那么点双连通分量怎么算呢?我们可以先来一个点双的图,来看看什么是点双连通分量。

这张图,如果进行点双的划分,应该是这样的:
| 点双连通分量编号 |
点双连通分量内容 |
| 一 |
1 2 3 4 |
| 二 |
4 5 6 |
| 三 |
7 8 9 |
| 四 |
7 10 |
有人就会说,你这是不是搞错了啊?为什么 $4,7$ 重复出现了?没有搞错,我们注意到上面说一个点双的分界线应该是删除后让图不连通的点。但是我们会发现,对于连通分量一,四点往外不论怎么扩散,都会存在一个删去后让图不连通的点,也就是四号点,所以说四号点使我们能取到的极限了,而对于联通分量二也是如此。所以说我们会得出一个结论:
原图中删去会使得原图不在联通的点,也就是我们常说的割点,属于多个连通分量。
这个结论很重要,后面讲点双缩点的时候,也需要用到。
那么这时候我们就发现了,如果我们还需要用 Tarjan 的方式去得到点双连通分量的话(也就是弹栈的形式)这时候一个点双的起点就不再是当 $low[u] = dfn[u]$ 的时候了,而是找到一个割点的时候。
所以说,我们要先求点双连通分量,我们需要优先知道怎么求割点。
那么首先,我们还是稍稍借用一下上面的图,不过这里对他进行一点点的处理:

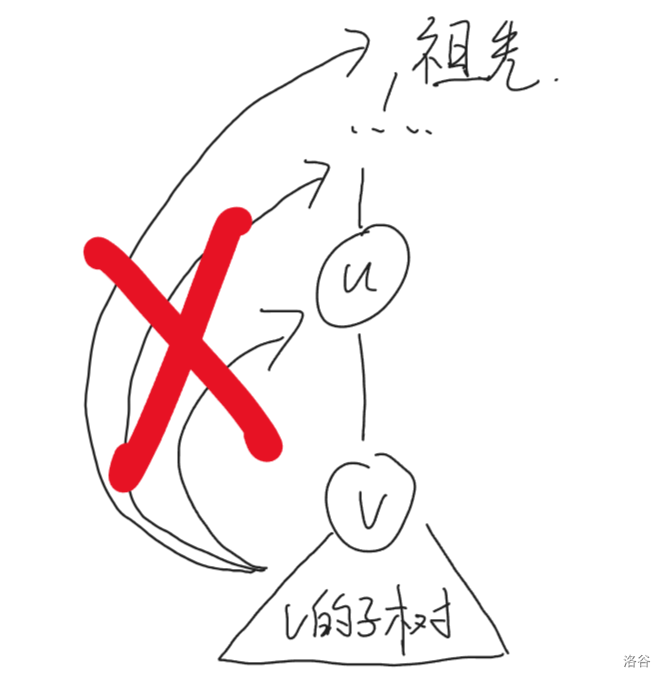
我们现在已经知道了这张图的割点是 $4,7$ 我们来看看他的性质。四和七,他们作为割点,我们可以在他们身上大致的经行猜想。他们肯定和割边类似,也就是说,他们的子孙,一定最多不会跑到他的上面,也就是说 $low[v]\ge dfn[u]$ 。这里和割边不一样的是,他可以取到等号,因为割边就是割边,他不允许儿子及其子孙可以连到父亲,这样就会出现环,而导致删除这条边后仍然联通;但是割点不一样,割点的消失会导致所有与其相连的边都不见,所以即使我的子孙可以连接到我也没关系,但是超过我就不可以了。
当然这里还有一个坑,就是根节点他一定满足上面说的要求,这时候怎么办?我们要看他有几个儿子,这里的儿子是指 Dfs 树上的儿子,也就是直接用树边连接的儿子,就比如上图,根节点 1 直观上来讲有两个儿子,2 和 4,但是连接他和 4 的是一条返祖边,返祖边并不能算作根的一个儿子,所以说 1 号点只有一个儿子,所以他不是割点,他如果是割点的话,至少要有两个树边儿子。这是要特判的。
而且我们发现,对于点双连通分量,我们不需要像边双一样担心会有边被重复计算,所以说,我们可以省略掉求边双用的标记边数组,而改为只要不走自己的父亲就可以了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int , int > pii;
typedef unsigned long long ull;
namespace FastIO
{
template<typename T> inline T read(T& x) {
x = 0;
int f = 1;
char ch;
while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
x *= f;
return x;
}
template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
read(x);
read(x_...);
return;
}
inline ll read() {
ll x;
read(x);
return x;
}
};
using namespace FastIO;
const int MaxV = 5e5 + 10;
const int MaxE = 2e6 + 10;
template<int N, int M>
class Graph {
private :
struct Edge {
int to, nt, wt;
Edge() {}
Edge(int to, int nt, int wt) : to(to), nt(nt), wt(wt) {}
}e[M];
int hd[N], cnte;
public :
inline void clear() { memset(hd, 0, sizeof(hd)), cnte = 0; }
inline void AddEdge(int u, int v, int w = 0) {
e[++cnte] = Edge(v, hd[u], w);
hd[u] = cnte;
}
inline int head(int u) { return hd[u]; }
inline int nt(int u) { return e[u].nt; }
inline int to(int u) { return e[u].to; }
inline int wt(int u) { return e[u].wt; }
};
int n, m;
Graph<MaxV, MaxE << 1> G;
inline void Input() {
read(n, m);
int u, v;
for(int i = 1; i <= m; i++) {
read(u, v);
if(u == v) continue;
G.AddEdge(u, v);
G.AddEdge(v, u);
}
}
int dfn[MaxV], low[MaxV], cntd;
stack<int >stk;
int cntc, col[MaxV];
vector<int >clb[MaxV];
int cut[MaxV];
void Tarjan(int u, int fa) {
dfn[u] = low[u] = ++cntd;
stk.push(u);
if(u == fa && G.head(u) == 0) {
clb[++cntc].push_back(u);
stk.pop();
return ;
}
int ch = 0;
for(int i = G.head(u); i; i = G.nt(i)) {
int v = G.to(i);
if(!dfn[v]) {
Tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) {
if(++ch >= 2 || u != fa) cut[u] = 1;
cntc++;
int now;
do {
now = stk.top();
col[now] = cntc;
clb[cntc].push_back(now);
stk.pop();
}while(now != v);
clb[cntc].push_back(u);
}
}
else if(v != fa) {
low[u] = min(low[u], dfn[v]);
}
}
}
inline void Work() {
int cnt = 0;
for(int i = 1; i <= n; i++) {
if(!dfn[i]) {
Tarjan(i, i);
}
if(cut[i]) cnt++;
}
printf("%d\n", cnt);
for(int i = 1; i <= n; i++) {
if(cut[i]) printf("%d\n", i);
}
}
int main() {
int T = 1;
while(T--) {
Input();
Work();
}
return 0;
}
|
这里注意一下,我们弹栈不可以弹到 u 点,是因为一些 Dfs 的顺序会导致栈里的一个点双连通分量的内容与割点之间间隔了内容,具体的话我这里有一组 hack 数据:
用这个模拟栈,就可以知道为什么说割点和点双连通分量的内容会有间隔。
然后其实求割点的代码也在里面了,这里不再重复。
点双连通缩点:真道正理
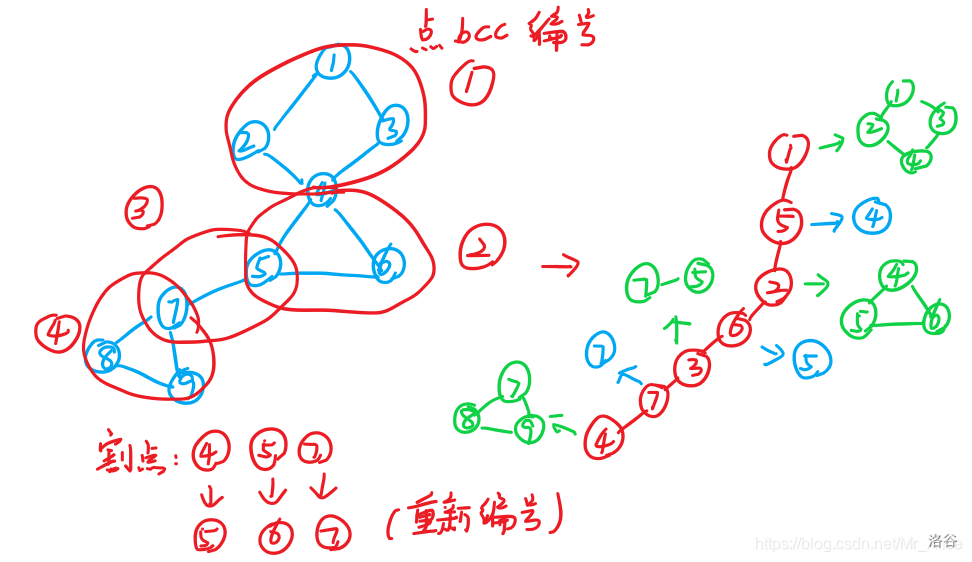
接下来就是点双缩点的内容了。点双缩点很难评,他也是一样,把一整个点双连通分量看作一个点,但是,我们发现割点同时处于多个连通分量怎么办?单独拿出来。我们可以做出下面的这张图表示过程:

这个的话,就是双缩点的图示。但是呢,这种缩点方式处理不到单个点,所以说我们有时候还会对于每一个代表点双连通分量的点,和其内部的所有点相连。这是一种叫做圆方树的表现形式,很好说。
这个就是缩点的实现图示,但是具体的实现其实也差不多,我下面放一个代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| int dfn[MaxV], low[MaxV], cntd;
stack<int >stk;
int cntc, col[MaxV];
vector<int >clb[MaxV];
int cut[MaxV];
Graph< MaxV << 1, MaxE << 1 >T;
void Tarjan(int u, int fa) {
dfn[u] = low[u] = ++cntd;
stk.push(u);
if(u == fa && G.head(u) == 0) {
clb[++cntc].push_back(u);
stk.pop();
return ;
}
int ch = 0;
for(int i = G.head(u); i; i = G.nt(i)) {
int v = G.to(i);
if(!dfn[v]) {
Tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) {
if(++ch >= 2 || u != fa) cut[u] = 1;
cntc++;
int now;
do {
now = stk.top();
T.AddEdge(cntc + n, now);
T.AddEdge(now, cntc + n);
col[now] = cntc;
clb[cntc].push_back(now);
stk.pop();
}while(now != v);
clb[cntc].push_back(u);
T.AddEdge(cntc + n, u);
T.AddEdge(u, cntc + n);
}
}
else if(v != fa) {
low[u] = min(low[u], dfn[v]);
}
}
}
|
这样的结构就可以让我们解决很多问题,有了树的结构,我们可以用树剖等各种树上算法去处理问题,也算是点双的必备技能之一。
算法实战:四灵捧圣
查看相关算法标签喵!
参考资料(以下排名不分先后):