前言:号 · 未授勋之花
本文更新于 【算法介绍】连通分量 | 祝馀宫 基础之上。如要阅读下面的内容,建议优先观看上文。本篇内容主要用更加通俗易懂的方式去表现出强连通分量的这个概念以及用 Tarjan 求强连通分量的思想。不会特别注重于讲解基础内容。
序章:武 · 赤角石溃杵
首先,我们回顾一下 Tarjan 算法的主要思想。Tarjan 算法的主要思想,是基于每一个点的 Dfs 序,以及对应的一些性质,去判断某一些边,某一些点,他们所代表的内容。
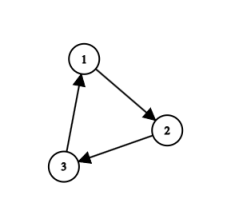
那么所谓强连通分量,就是指有向图中,如果两个点可以互相到达,那么称他们是强连通的,他们就是在同一个强连通分量。对于强连通分量在有向图中,最直观的结构,就是环。

首章:花 · 华馆梦醒形
首先我们现在给出一个设定,点的颜色:黑白灰。我们定义一个未走的点是白色,走了但是没有回溯回来的是灰色,完全走完的是黑色。那么我们可以有新的定义表示有向图中的四种边。
- 树边:显然的是当前的点指向了一个白色的点。
- 返祖边:我们当前的点指向了灰色的点。
- 前向边:当前的点指向黑色的点。
- 横插边:当前的点指向黑色的点。
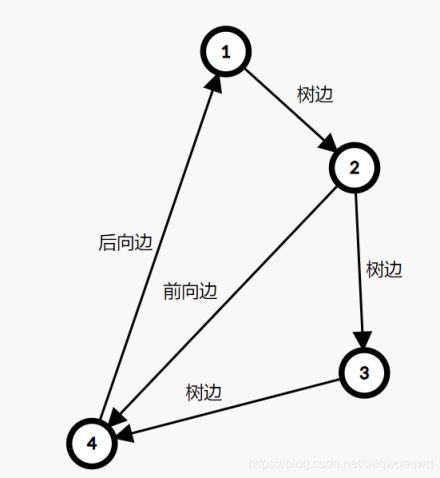
具体的我们可以看下面的这张图来理解:

我们的深搜以 $1\rightarrow2\rightarrow3\rightarrow4$ 进行。那么我们到了 $4$ 的时候就会发现,他连到的点 $1$ 已经开始了搜索但是还没回溯,也就是灰色点,那么这条边就是所谓的后向边,也就是常说的返祖边。然后我们开始回溯,从四回溯到三,从三回溯到二。这时候三四都已经回溯,被标记成了黑色点,然后就发现二的还有个点,也就是我们说的前向边,它指向的四其实是一个黑色节点。树边很明显,每次访问之前这个点一定是白色的。
这个图片中没有表现出来的横插边和前向边特别像。上面的定义中我们说他们指向的都是黑色节点,而黑色节点的区别在于横插边指向的两个节点不在一个子树,前向边连接的两个点是祖先和子孙关系。那么我们判断两个点是否是在同一个子树,或者说是不是子孙关系,有两种方式:
- 第一种就是我刚刚提到的染色方式
- 第二种就是用 Dfs 序,记录每一个点的起始位和结束位,在同一个子树的这个区间,一定是包含关系;不在同一个子树,一定是完全不相交。这种类似于括号序列的形式,就是 Dfs 序的一大特性。
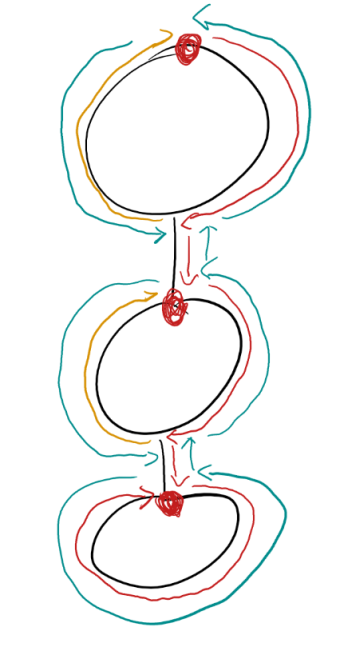
我们在区分出所有的边之后,考虑如何实现,进一步挖掘性质。如果一个强连通分量的第一个点,被访问了,那么这一个强连通分量的所有点都会被访问,但是访问的顺序就不一样了,因为我们是 Dfs 序,也就是实现过程是 Dfs ,我们的访问顺序,就是下图所示:

这个长得像糖葫芦一样的图片,就是我们深搜的过程,下面给出每一种颜色的定义:
- 黑圈圈:一个强连通分量
- 黑边边:连接两个强连通分量的边
- 红点点:每一个强连通分量第一个被访问的点
- 红箭头:第一次深搜过程
- 蓝箭头:回溯过程
- 黄箭头:回溯后对于未访问完的点的访问
我们来看看他是怎么深搜的:
- 首先一条红边下到底,出现了三个红点,这三个红点是这个强连通分量第一个被访问的点,尤为重要,后面会讲为什么
- 然后出现了最下面的蓝边。因为最下面的强连通分量搜完了,开始回溯
- 回溯到了最下面的强连通分量的第一个点,然后往上回溯到第二个,开始对于第二个强连通分量剩余点的搜索
- 第二个强连通分量搜完了,开始回溯
- 回溯到了第二个强连通分量的第一个点,往上回溯到第一个强连通分量,然后开始对于第一个强连通分量剩余部分的搜索
- 搜完了,回溯。
仔细观察这个过程,我们会发现,强连通分量的统计顺序,是最后访问的,最先被记录。也就是说,强连通分量的统计顺序是后进先出,也就是栈的结构。这也给了我们用栈来记录每一个点的想法。
那么如果我们用了栈来记录每一个点,其实一开始定义的颜色也就不需要了。因为所谓黑色点,就是访问了退出栈了的点;白色点就是未访问不在栈里的点;灰色点,就是访问了在栈里的点。这样我们就完成 Tarjan 求强连通分量的初步构建。
次章:御 · 心护护心铠
接下来就是进一步的 Tarjan 求强连通分量的推导。首先我们知道,标记点其实是不必要的,因为如果一个点未走过,他的 $\tt dfn$ 一定是 $0$ ,我们最小的 Dfn 值都是从 1 开始算的,所以 Dfn 是 0 的一定是没有访问过。那么根据新的规则,我们可以得到这样的思路,去分辨有向图的四种边:
- 树边:指向 dfn 为 0 的点
- 返祖边:指向 dfn 不为 0 并且在栈里的点
- 前向边:指向 dfn 不为 0 且不在栈里的点
- 横插边:指向 dfn 不为 0 且在栈里,但是栈中位置一定在这个强连通分量起始点更深的位置的点
不难发现,能够判断环的,一定只有树边和返祖边,显然的另外两种边都是非必要的。一个环,它最明显的特点,就是最终会和起点连到一起。而根据我们深搜的顺序,起点一定是这个强连通分量中 dfn 值最小的点。所以说,我们可以定义一个数组 low ,它用来记录当前点以及当前点的子孙所能到达的 dfn 最小的点。
那么我们就发现了,如果他是一个强连通分量,他的 low 值一定等于 dfn 值。这样的话,我们就能判断一个强连通分量了。接下来就是开始退栈,我们每访问一个节点,就把他们放到栈里,这样存储顺序是 Dfs 序。然后找到了强连通分量就开始退栈,每次退栈就退到这个强连通分量的起点。这样就可以标记完了,这也是 Tarjan 求强连通分量的全过程了。
尾章:攻 · 旋风大扫除
那么这里就献上一份详细注释的 Tarjan 求强连通分量模板题:B3609 图论与代数结构 701 强连通分量 - 洛谷 的代码,自行感性理解一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int , int > pii;
typedef unsigned long long ull;
namespace FastIO
{
template<typename T> inline T read(T& x) {
x = 0;
int f = 1;
char ch;
while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
x *= f;
return x;
}
template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
read(x);
read(x_...);
return;
}
inline ll read() {
ll x;
read(x);
return x;
}
};
using namespace FastIO;
const int MaxV = 1e4 + 10;
const int MaxE = 1e5 + 10;
template<int N, int M>
class Graph {
private :
struct Edge {
int to, nt, wt;
Edge() {}
Edge(int to, int nt, int wt) : to(to), nt(nt), wt(wt) {}
}e[M];
int hd[N], cnte;
public :
inline void AddEdge(int u, int v, int w = 0) {
e[++cnte] = Edge(v, hd[u], w);
hd[u] = cnte;
}
inline int head(int u) { return hd[u]; }
inline int nt(int u) { return e[u].nt; }
inline int to(int u) { return e[u].to; }
inline int wt(int u) { return e[u].wt; }
};
int n, m;
Graph< MaxV, MaxE >G;
inline void Input() {
read(n, m);
int u, v;
for(int i = 1; i <= m; i++) {
read(u, v);
G.AddEdge(u, v);
}
}
int dfn[MaxV], low[MaxV], cntd;
stack<int >stk; int instk[MaxV];
int cntc, col[MaxV];
vector<int >clb[MaxV];
void Tarjan(int u) {
dfn[u] = low[u] = ++cntd;
stk.push(u), instk[u] = 1;
for(int i = G.head(u); i; i = G.nt(i)) {
int v = G.to(i);
if(!dfn[v]) {
Tarjan(v);
low[u] = min(low[u], low[v]);
}
else if(instk[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]) {
++cntc;
int v = stk.top(); stk.pop();
while(v != u) {
col[v] = cntc;
instk[v] = 0;
clb[cntc].push_back(v);
v = stk.top(); stk.pop();
}
col[v] = cntc;
instk[v] = 0;
clb[cntc].push_back(v);
}
}
inline void Work() {
for(int i = 1; i <= n; i++) {
if(dfn[i] == 0) {
Tarjan(i);
}
}
printf("%d\n", cntc);
for(int i = 1; i <= n; i++) {
if(clb[col[i]].empty()) continue;
sort(clb[col[i]].begin(), clb[col[i]].end());
for(auto &p : clb[col[i]]) {
printf("%d ", p);
}
printf("\n");
clb[col[i]].clear();
}
}
int main() {
int T = 1;
while(T--) {
Input();
Work();
}
return 0;
}
|
后记:性 · 女仆的态度
这个就是本文的全部内容了,希望能让大家有更好的理解。