算法简介：开拓的心魂

区间类动态规划，是作为线性动态规划的拓展。与线性不同的是，区间类动态规划的递推操作，可以是任意的。当我们发现这样的一道例题出现了有可以分为两个子区间合并的这样的性质，且满足最优子结构和无后效性，就是区间类动态规划的题目了。

算法演示：烈火与勇气

例题选讲：冒险憧憬

那么首先的，作为动态规划的题目，最好的方式还是通过例题去理解这样一个算法的大致特点。

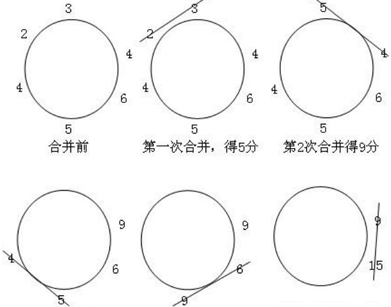
将 $n(1≤n≤200)$ 堆石子绕圆形操场摆放，现要将石子有次序地合并成一堆。规定每次只能选相邻的两堆石子合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

  1. 选择一种合并石子的方案，使得做 $n-1$ 次合并，得分的总和最小。
  2. 选择一种合并石子的方案，使得做 $n-1$ 次合并，得分的总和最大。

例题思路：踏破绝境

那么首先拿到一道 DP 题，一般都会给人一种贪心的假象，这题也不例外。尤其是收到合并果子那道题的影响，有些人可能根本不会想到 DP 去，贪心的做法确实很难找到一种可以推翻掉他的数据。

那么这里先给出一个感性的证明，就是给出这个贪心错误的数据。首先明确一点：贪心策略是每次合并相邻的较小的两堆（如果是让答案最小的话）

1
2
3
// The Example can break the Greedy Algorithm
// n = 6
// a = { 3, 4, 6, 5, 4, 2 }

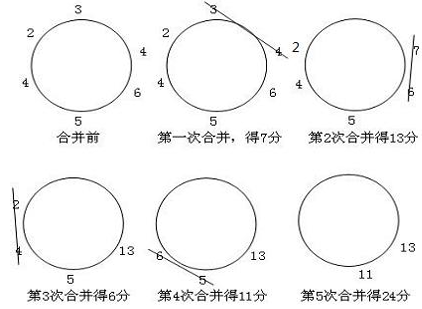
我们试试先模拟一下贪心的解法：

贪心错解

算一算这个贪心算出来就是 $62$ 的答案。那么正确的划分是多少呢？

手模正解

这样的解法，应该是 $61$ 的。确实比贪心要少，那么这样就是感性的证明了贪心为什么是错误的。

那么我们有为什么选择 DP 呢？

例题正解：火热激情

我们考虑若最初的第 $L$ 堆石子和第 $R$ 堆石子被合并成一堆，则说明 $L$ ~ $R$ 之间的每堆石子也已经被合并，这样 $L$ 和 $R$ 才有可能相邻。因此，在任意时刻，任意一堆石子均可以用一个闭区间 $[L,R]$ 来描述，表示这堆石子是由最初的第 $L$ ~ $R$ 堆石子合并而成的，其重量为 $∑\limits_{i = L}^{R}a_i$ 。

另外，一定存在一个整数 $k$ ，在这堆石子形成之前，先有第 $L$ ~ $k$ 堆石子（闭区间 $[L,k]$ ）被合并成一堆，第 $k+1$ ~ $R$ 堆石子（闭区间 $[k+1,R]$ ）被合成一堆，然后这两堆石子才合并成[L,R]。

这样的模型对应到动态规划中，就是两个长度较小的区间上的信息向一个更长的区间发生了转移，划分点 $k$ 就是转移的决策，区间长度 $len$ 就是 DP 的阶段。

不过，区间长度可以由左端点和右端点表示，即 $len=R-L+1$ 。根据动态规划 “选择最小的能覆盖状态空间的维度集合” 的思想，我们可以只用左、右端点表示 DP 的状态。

设 $sum[i]$ 表示从第 $1$ 堆到第 $i$ 堆石子数总和。
$Fmx[i][j]$ 表示将第 $i$ 堆石子合并到第 $j$ 堆石子的最大得分；
$Fmi[i][j]$ 表示将从第 $i$ 堆石子合并到第 $j$ 堆石子的最小得分；
则有状态转移方程:

这样的时间复杂度为 $O(n^3)$ 。

例题代码：热情不灭

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
using namespace std;

const int N=310;

int n;
int a[N];
int d[N];
int dp1[N][N];
int dp2[N][N];

void Input(){
	scanf("%d", &n);
	for(int i=1; i<=n+n; i++){
		scanf("%d", &a[i]);
        a[i+n]=a[i];  
        d[i]=d[i-1]+a[i];
	}
}

void Work(){
    for(int len=1; len<n; len++){ 
        for(int i=1, j=i+len; (j<n+n) && (i<n+n); i++, j=i+len){  
            dp2[i][j]=999999999;  
            for(int k=i; k<j; k++){  
                dp1[i][j] = max(dp1[i][j], dp1[i][k]+dp1[k+1][j]+d[j]-d[i-1]);   
                dp2[i][j] = min(dp2[i][j], dp2[i][k]+dp2[k+1][j]+d[j]-d[i-1]);  
            }  
        }  
    }  	
    int mi=999999999, mx=0;  
    for(int i=1; i<=n; i++){  
        mx=max(mx, dp1[i][i+n-1]);  
        mi=min(mi, dp2[i][i+n-1]);  
    }  
	printf("%d\n%d", mi, mx);    
}

int main(){
	Input();
	Work();
    return 0;
}

算法实战：无畏的热血

查看相关标签喵！