算法简介：堆叠真空域

在做题的过程中，我们经常会发现那些看上去是纯暴力，但是复杂度却是 $n\log n$ 或者其他的算法或思想。这些题抓住了做题人在计算复杂度时候的失误，从而达到了思维难度提升的效果。他们通常题目评级不高，但是却总是很难想到。

算法演示：不羁型贝特

大致思想：零失误少女

这类题目有一大特点：倍增

比如说这些题目 P9974【USACO23DEC】Candy Cane Feast B 、【ABC315F】Shortcuts 等等等等，他们的题目或多或少都点到了一个关键字二的幂次、翻倍。比如说 USACO 的这道，虽然没有直接提到翻倍，但是我们会注意到奶牛最多吃到和自己一样高的糖果，也就是说第一只奶牛会一直翻倍，这也保证了复杂度。

这样倍增的性质，通常是隐蔽的，有些甚至感觉微小的不可发现，这也是成就了这些题目难度的主要因素。而这种倍增是丰富多样的，比如说刚刚给出的第二题，跳过的代价显而易见是极高的，我们发现最大距离会远小于跳过多个点，更具这个性质，我们可以把题目的空间以及时间复杂度压到 $\log n$ 。这是一种倍增代价，去发现优劣的思路。

除此之外，比如说启发式合并，每次合并较小的就可以在 log 的复杂度内搞定，这些算法也是因为不断的使小区间至少翻一倍大，使得复杂度越来越低。

也就是说，倍增（或者说翻倍）的思想，是无处不在的，我们再做题的时候需要仔细分析复杂度，去找到这个可压缩的点，千万不能搞错了。

例题之一：炼金的偏执

大致题面

Farmer John 的奶牛对甜食情有独钟，它们尤其喜欢吃糖果棒。FJ 共有 $N$ 头奶牛，每头奶牛都有一个特定的初始高度。他想要喂它们 $M$ 根糖果棒，每根糖果棒的高度也各不相同（$1 \le N,M \le 2\cdot 10^5$）。

FJ 计划按照输入给出的顺序，逐一喂给奶牛们糖果棒。然后，奶牛们会按照输入给出的顺序一个接一个地排队，走向糖果棒，每头奶牛最多吃到与它高度相同的部分（因为它们够不到更高的地方）。即使奶牛吃掉了糖果棒的底部，糖果棒也在最初悬挂的地方保持不动，并不会被降低到地面。如果糖果棒的底部已经高于某头奶牛的高度，那么这头奶牛在它的回合中可能什么也吃不到。每头奶牛轮流吃过后，它们的身高会增加它们吃掉的糖果棒的单位数量，然后农夫约翰挂上下一根糖果棒，奶牛们再次重复这个过程（第一头奶牛再次成为第一个开始吃下一根糖果棒的）。

题目思路

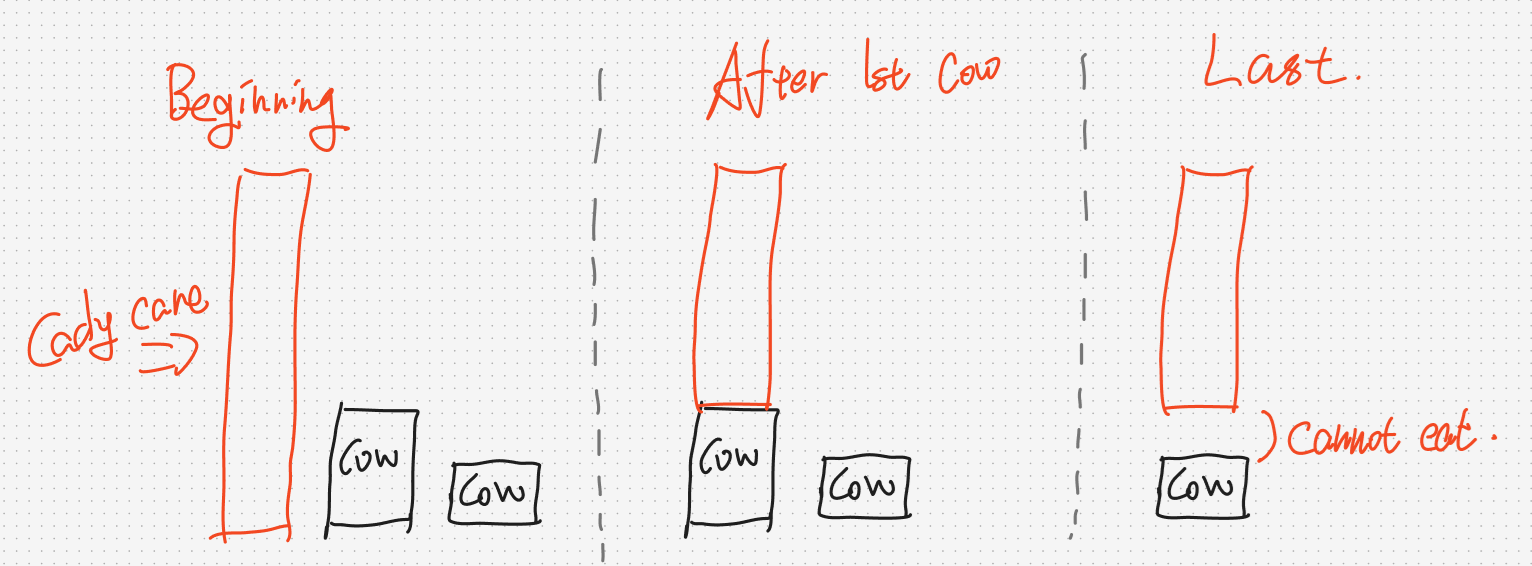
题目意思，很简单，就是让奶牛一轮一轮吃过去，只不过呢，糖果是悬在天上的，前面的奶牛吃掉了一段长度，就有可能会导致后面的奶牛吃不到糖果，大概有如下示意图：

题意演示

这张图很显然的模拟出了奶牛吃糖果的情形（没有画出奶牛一吃完后长高的样子）如果前面的奶牛存在一个特别高的，就会导致后面矮的吃不到任何糖果，那么想要解决问题，就只能模拟了。这样的话复杂度似乎是 $O(n^2)$ （ $n,m$ 同阶所以写作 $n^2$ ），过不了这道题啊，这怎么办？

仔细想想，这样做的复杂度，真的是 $O(n^2)$ 吗？既然这么问了，显然不是，我要是说这个的复杂度是 $O(n\log 1e9)$ 你信吗？为什么是 $\log $ 复杂度，不应该罢。我们注意到，所有牛都有可能吃不到，但是有一头牛，他一定能吃到糖果，那就是第一只牛。第一支牛一定可以吃到等同于自己高度的糖果并长到自己一倍的长度。这时候，出题人的目标就已经显现出来了，这是一道伪装成暴力算法的题目，就是考验做题人能不能看出这一点并 AC 。第一只奶牛一倍一倍的长，显而易见的至多 32 次就可以超过糖果的最高高度 $1e9$ ，我们只需要模拟的时候判断糖果是否吃完就可以。至此，题目解决。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

const int N = 2e5 + 10;

int n, m;
ll a[N], b[N];

inline void Input() {
    read(n, m);
    for(int i = 1; i <= n; i++) {
        read(a[i]);
    }
    for(int i = 1; i <= m; i++) {
        read(b[i]);
    }
}

inline void Work() {
    for(int i = 1; i <= m; i++) {
        ll ate = 0;
        for(int j = 1; j <= n; j++) {
            if(a[j] > ate) {
                if(b[i] + ate < a[j]) {
                    a[j] += b[i], b[i] = 0;
                    break;
                }
                b[i] -= a[j] - ate;
                ll add = a[j] - ate;
                ate = a[j];
                a[j] += add;
            }
        }
    }
    for(int i = 1; i <= n; i++) {
        printf("%lld\n", a[i]);
    }
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

例题之二：认真普通瓶

大致题面

对于平面坐标上 $n$ 个点，输出从 $1$ 走到 $n$ 的代价。两点直线距离为欧几里得距离。

正常来讲，你的路径应该为 $1 \to 2\to 3 \to \cdots \to (n-1)\to n $，你的代价即为你走过的距离。

但是你被允许跳过一些点，使路径变为 $1\to 2\to \cdots \to (x-1) \to (x+1) \to \cdots \to (n-1) \to n$，跳过的点数不限，但 $1$ 号点和 $n$ 号点不能被跳过。

跳过操作需要花费，此时你的代价为你走过的距离加跳过产生的花费。

跳过的花费如下定义：

对于整个旅途，如果你跳过 $c$ 个点，设花费为 $S$，

  • $c=0$ 时 $S=0$；
  • $c>0$ 时 $S=2^{c-1}$。

输出从 $1$ 走到 $n$ 的最小代价。

题目思路

那么这题显而易见是不难的，我们可以很容易的想到一个动态规划状态 $dp[i][j]$ 表示前 $i$ 个点跳过 $j$ 个的最小代价，然后显然多跳过了一个点的时候从 $2^{j-1}$ 到 $2^j$ 这个花费不好计算，所以说在最后的时候再统计。

但是，这样显而易见复杂度非常不正确。于是，我们再次把目光看向跳过花费 $S = 2^{c-1}$ 。每个点的坐标取值范围是 $[0,1e4]$ 可以根据勾股定理得到两个点的最大距离也就是 $1e4$ 多一点的范围，一共也就 $1e4$ 个点，也就是说最长最长总路程也就 $1e8\sim 1e9$ 我们就算是算他有 $1e9$ 但是两倍两倍翻倍算，也就最多翻 $32$ 次的机会，也就是说，当我们跳过比 $32$ 个点还要多的时候，跳过点就已经不再优秀了，这样也就可以把状态压到 $dp[i][32]$ 的大小，通过此题。

示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
double dp[N][50];

inline double Dis(int i, int j) {
    return sqrt(
        1.0 * (a[i].first - a[j].first) * (a[i].first - a[j].first) + 
        1.0 * (a[i].second - a[j].second) * (a[i].second - a[j].second) );
}

inline void Work() {
    for(int i = 0; i <= n; i++) {
        for(int j = 0; j <= 25; j++) {
            dp[i][j] = 1e9;
        }
    }
    dp[1][0] = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j < min(25, i); j++) {
            dp[i][j] = min(dp[i][j], dp[i - 1][j] + Dis(i - 1, i));
        }
        for(int j = 1; j < i - 1; j++) {
            for(int k = i - j - 1; k <= 25; k++) {
                dp[i][k] = min(dp[i][k], dp[j][k - (i - j - 1)] + Dis(i, j));
            }
        }
    }
    double ans = dp[n][0];
    for(int i = 1; i <= 25; i++) {
        ans = min(ans, dp[n][i] + (1LL << (i - 1)));
    }
    printf("%lf", ans);
}

算法总结：混元熵增论

其实吧，这个技巧还是广泛而出其不意的。刚刚动规的那道题，主要思路就是存在一种情况使得一个选择不再优秀，这就让我想到了曾经做过的题目，让你用一个马一个炮杀死一个子，显然我们有跳马或者移动炮两种选择。但是我们会发现如果棋盘超过了某个边界值，跳马不在优秀，所以只能用炮了。

这种找到题目极限的思想，是一种很新同样也很具备思维难度的思想，希望以后可以多多注意。