题面
大秦为你打开题目传送门
题目描述
小朋友要玩,卡卡颂。
在开始游戏之前他们要拼地图,有 $n$ 行 $m$ 列的格子,每个格子上有一个小方块,每个小方块的四条边可能是城市 $(C)$ ,道路 $(R)$ 或者空地 $(F)$ 。现在要求旋转这些小方块,使得相邻的小方块对应的边上是相同的建筑。
问有多少种旋转方案,不准对方块翻转,不准交换方块的位置。
思路
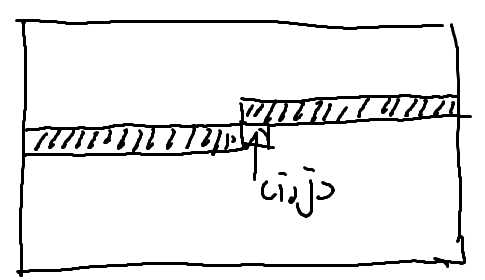
这题也是直接一眼轮廓线DP,直接处理出所有方块旋转以后的值,然后处理出这个轮廓线边缘的所有值,由于三进制的计算十分的复杂,我这里就直接用了字符串来处理。我用 $1$ ~ $m$ 表示这个轮廓线的底边的值,再用 $m + 1$ 表示这个轮廓线突出来能看到的这个右边的边(如下图)

这样就简单了,直接递归做就可以了,算是一个非常玄学的代码了,,
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef __int128 int128;
namespace FastIO
{
template<typename T> inline T read(T& x) {
x = 0;
int f = 1;
char ch;
while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
x *= f;
return x;
}
template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
read(x);
read(x_...);
return;
}
inline ll read() {
ll x;
read(x);
return x;
}
};
using namespace FastIO;
const int P = 1e9 + 7;
struct Cube{
char lt , rt , dw , up;
Cube(char a = 'A' , char b = 'A' , char c = 'A' , char d = 'A'){
up = a , dw = b , lt = c , rt = d;
}
};
int n, m;
Cube a[20][20][4];
map<string , ll> dp[20][20];
inline void Input(){
read(n, m);
char s[5];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
scanf("%s", s);
a[i][j][0].up = s[0];
a[i][j][0].rt = s[1];
a[i][j][0].dw = s[2];
a[i][j][0].lt = s[3];
}
}
}
inline ll DP(int i , int j , string mask){
if(i > n) return 1;
if(dp[i][j].find(mask) != dp[i][j].end()) return dp[i][j][mask];
ll ans = 0;
for(int k = 0; k < 4; k++){
if((a[i][j][k].up == mask[j] || i == 1) && (a[i][j][k].lt == mask[m + 1] || j == 1)){
string ts = mask;
ts[m + 1] = a[i][j][k].rt;
ts[j] = a[i][j][k].dw;
if(j+1 <= m) ans = (ans + DP(i, j + 1 , ts)) % P;
else ans = (ans + DP(i + 1 , 1 , ts)) % P;
}
}
return dp[i][j][mask] = ans % P;
}
inline void Work(){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
for(int k = 1; k < 4; k++){
a[i][j][k].up = a[i][j][k-1].lt;
a[i][j][k].rt = a[i][j][k-1].up;
a[i][j][k].dw = a[i][j][k-1].rt;
a[i][j][k].lt = a[i][j][k-1].dw;
}
}
}
string s = " ";
for(int i = 1; i <= m + 1; i++) s += 'A';
printf("%lld\n" , DP(1, 1, s) % P);
}
int main(){
int T = 1;
while(T--) {
Input();
Work();
}
return 0;
}
|