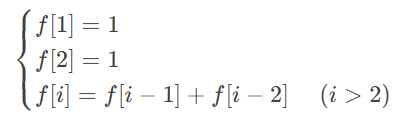算法简介： DP 与算法之歌

所谓 DP 也就是 $\tt Dynamic\ Programming$ 的缩写，即动态规划算法。我们常说的动态规划，它是一种基于把一个问题分为多个子问题，通过权衡他们之间的最优，得到最后的最优。而这种做法和我们一开始学过的暴力枚举的区别就在于 —— $\tt DP$ 数组。$\tt DP$ 的核心就是把子问题分解为不相互独立的子问题后，使用数组记录最优解，从而减少计算次数的一种算法。穷举法也可以称为静态规划。对于和 DP 特别像的另外两个算法，也就是贪心和分治。贪心，是一种对于每一步都取最优解，最后使得总答案最优的算法。他和 DP 的区别是，DP 为了求全局最优，可以适当舍弃一部分的最优解，而贪心不行。分治算法，是把问题分为相互独立的子问题计算，这一点与 DP 是不同的。而对于 DP 算法，我们完全不需要有那么多的顾忌，不要以为他是英文的名称就很高大上，我们只需要知道，它不过是存下了每一步的答案去权衡最优解罢了。DP 其实并没有特别的拘泥于一些模板，所以没有太多需要记的东西，我们只需要一个灵活的大脑。

算法演示：递推递归千题间

对于 DP 的几种常见形式，我们需要以几个常见的问题切入。最开始的，因为其需要分子问题，记录答案，合并答案，我们不由自主的想到一种东西：搜索。

万能记搜，恒常乐土

我们从一个最最基础的东西开始。搜索天生的具有这些性质，我们可以尝试用这种东西解决一些基础的例子。比如说现在给出斐波那契数列的地推式子：

对于这个式子，不难写出其递归代码。

1
2
3
4
5
ll feb(int n) {
    // cout << n << endl; // 打表用
    if(n <= 2) return 1;
    return feb(n - 1) + feb(n - 2);
}

上述的代码显而易见是会超时的。具体的复杂度分析我们可以大概的打表看看 $n = 5$ 的情况。

代码输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5
4
3
2
1
2
3
2
1
总计：
5 ： 1次
4 ： 1次
3 ： 2次
2 ： 3次
1 ： 2次

这样重复的数据在 $n$ 更大的时候会更加明显，我们要拒绝这样的事发生。重新回顾一下我们的 $\tt DP$ 算法核心：记录答案。那么我们就可以记数组 $feb_i$ 表示的是第 $i$ 个斐波那契数的值，这样如果某一个值已经计算过，就不必接着递归找了，这样大大减少了递归的量，代码如下：

1
2
3
4
5
6
7
8
memset(dp, -1, sizeof(dp));
ll feb(int n) {
    // 这里就是 DP 搜索的精髓，如果记录过答案的话就直接return，相当于就不需要往下递归了
    if(dp[n] == -1) return dp[n];
    // cout << n << endl; // 打表输出递归的量
    if(n <= 2) return dp[n] = 1;
    return dp[n] = feb(n - 1) + feb(n - 2);
}

这样的话我们打表输出递归的量。

代码输出：

1
2
3
4
5
5
4
3
2
1

这样的话，我们的复杂度就掉到了 $O(n)$

无念无想，泡影断灭

那么除了递归的做法，就是递推了。观察递归的结构不难发现由于其嵌套的结构，基本上写完了就是写完了，完全没有优化的空间，相对的，递推的做法就会不太直观但是方便于优化。我们还是举斐波那契数列的例子。对于斐波那契，我们已经有了递推式，其实就是设一个数组记录了这个第 $i$ 个斐波那契数列的答案，按照给出的式子递推。不难写出如下的代码。

1
2
3
4
5
int dp[N]; // dp[i] 表示 第i个斐波那契数的值
dp[1]=dp[2]=1; // 初始值
for(int i = 3; i <= n; i++) { // 按照式子递推
    dp[i] = dp[i - 1] + dp[i - 2];
}

我们发现这样的代码具有一个特殊的形式：从多个已知答案递推到一个未知答案。这就是动态规划常见的多对一递推形式。这样的形式需要经过一定程度的分类讨论和思考。

不论是递归的记录答案还是递推的 DP 数组 ，我们在动态规划类的问题中，将其称为状态。
而递推答案的式子，就像刚刚代码中的 $dp[i]=dp[i-1]+dp[i-2]\ \ \ \ \ \ \ \ (i\ge3,i∈N^)$ 这个被称为动态规划*转移方程。

这两个东西都具有较强的思维性，需要慎重考虑。我们可以大概的看一个例题简单了解。

例题：铺地板

我们有两种方块，一种是 $2\times 2$ ，一种是 $2\times1$ ，问铺满 $2\times n$ 的矩阵有多少种不同的摆法。

首先拿到一道 $\tt DP$ 题目，要设计状态。我们设 $dp_i$ 表示铺满 $2\times i$ 的方案数。在设计状态的时候首先考虑能不能直接表示答案，这样是最好的，因为如果不做什么优化的话，一般来讲你从一个状态到另外一个状态这个枚举状态的过程，就是你设置 $dp$ 数组的维度大小。如果是像刚刚那样设状态的话我们发现这是可以做的，答案应该是 $dp_n$ 。

然后就是设计方程，我们要开始分类讨论结果了。首先这道题目肯定是多对一的递推方便，我们有几种选择：

  1. 从 $2 \times (i -1)$ 的图转移过来，就只有 $1$ 种方式，也就是竖着放一个 $2 \times 1$ 的方块，这样对于答案造成的贡献是 $1$ 。
  2. 从 $2\times(i-2)$ 的图转移过来，有 $2$ 种方式，放一个 $2\times2$ 或两个 $2\times1$ 这样可以保证铺满，可以继续递推，对于答案造成的贡献是 $2$ 。
  3. 此时不难发现，接下来的像 $(i - 3),(i-4)$ 什么的，有已经没有意义，都是从如上两种形式出来，不会有别的，所以说，转移方程式子如下：

接下来考虑初始值，首先当 $i = 1$ 的时候，$dp[1] = 1$ 就只有一种摆放方式。当 $i = 2$ 的时候，$dp[2] = 2$ 就是如上说的两种。

至此，这道 $\tt DP$ 宣告结束。

千手百眼，多向递推

那么刚刚说的是多对一的递推方式，那么既然有多对一，就一定有一对多，这种做法相对于多对一，一对多是一种我到那里去的形式。

为了解释这一种方式，我们可以整活性质地在写一次斐波那契。。。为什么说是整活性质呢，因为这种低级的递推题目，一对多就有点小题大作了。

那么这时候就不能用上面的递推式子了，我们考虑对于第 $i$ 个斐波那契数会对什么答案造成贡献。显而易见的，对于第 $i$ 给斐波那契数，会被第 $i + 1$ 和 $i + 2$ 相继采用，那么还是设 $dp[i]$ 表示第 $i$ 个斐波那契数列的值，可以写出如下代码：

1
2
3
4
5
6
dp[1] = dp[2] = 1;
for(int i = 1; i <= n; i++) {
    if(i + 1 != 2) dp[i + 1] += dp[i];
    dp[i + 2] += dp[i];
    // cout << dp[i] << ' ';
}

这就是这样写出来的纯弱智代码，仅仅图一个乐子（（（（

但是基本的考虑都是要有的，对于多对一和一对多这是需要看情况来分的，你觉得哪一种顺手，就用那个。但是万变不离其宗，只需要知道，所谓 $\tt DP$ 也不过是记录答案罢了。

算法实战：拾题杂谈—动规

见标签，分类喵！