文章总览：一心

平衡树是我 114514 年前就说要学的知识点，结果拖到现在……甚至这个封面都是今年春节前就做好了qwq。因为我太菜了，这篇文章主要讲的内容是普通的二叉搜索树和两种 Treap（或许封面得改成 Treap 专题？

下为本文大纲：

  1. 二叉搜索树概念简介
  2. 二叉搜索树分段推导
  3. 二叉搜索树优劣分析
  4. 无旋 Treap 基本概念
  5. 无旋 Treap 思想模拟
  6. 无旋 Treap 区间操作
  7. 无旋 Treap 综合例题
  8. 带旋 Treap 思想简介
  9. 带旋 Treap 分段实现
  10. 带旋 Treap 代码一览
  11. 两类 Treap 对比分析

前置知识：二观

概念讲解：幽府

说起二叉搜索树，各位并不陌生，在很久很久以前，我曾写过这样一篇文章：

友情链接：

【算法介绍】笛卡尔树 | 祝馀宫

这里面提到的笛卡尔树，也是二叉搜索树的一种。不过那篇文章并没有详细解释二叉搜索树的详细定义与编码方式，所以说作为平衡树重要的前置知识，我们把二叉搜索树一并在这里讲了。

首先我们来简单介绍一下二叉搜索树的概念。

  1. 规定每个节点有一个附加权值。
  2. 左子树和右子树都是二叉搜索树。
  3. 左子树上所有点的附加权值都小于其根节点的附加权值
  4. 右子树上所有点的附加权值都大于其根节点的附加权值
  5. 特殊的，空树也是二叉搜索树。

看上去很玄学，但是说白了就是，二叉搜索树的中序遍历是严格递增的，而且中序遍历严格递增的树也一定是二叉搜索树。而这一个性质也让我们可以完成很多的事情，最典型的就是根据左右子树的大小关系来寻找点，或者寻找第 K 大的值等等等等，有点类似于二分。

所以接下来我们来简单实现以下关于二叉搜索树的各项操作。

分段推导：录事

那么作为一个树形数据结构，它的操作无非就是最基础的增删改查，具体的操作总类可以右边的侧栏上。接下来我们来介绍较为基础的二叉搜索树实现。

节点定义

首先来看节点的定义，不难发现，二叉搜索树每一个节点的信息应该是不算少的，首先最最基础的是树的基本信息，左右儿子、节点权值、子树大小之类的。

另外的话，其实有一个小细节，那就是由于二叉搜索树的中序遍历要求严格递增，所以它内部不可能会有重复元素，这时候我们要存储重复元素的话，就需要保存重复元素数量的变量。

另外的话我感觉就没什么特殊的了，如果题目特殊要求可以增加一些要维护的信息。

1
2
3
4
5
6
7
struct TreeNode {
    int val; // 权值
    TreeNode *ls, *rs; // 左右儿子
    int cnt, sz; // 重复数量，子树大小
    TreeNode(int val)
      : val(val), size(1), count(1), left(nullptr), right(nullptr) {}
}

元素搜索

类似于二分，很简单。

1
2
3
4
5
6
bool search(TreeNode *p, int x) {
    if(p == nullptr) return false;
    if(p->val == x) return true;
    if(p->val > x) return search(p->ls, x);
    else return search(p->rs, x);
}

元素搜索看似不重要，但是删除等一系列修改操作都需要以搜索为前提，不然会有非法操作。

除了基本的元素搜索，还有两个可能会有用的函数，就是极值查询，这个会在后面讲到为什么会用，先来想一下代码怎么写。我们在二叉搜索树的概念中讲到，“中序遍历是递增的”是“某一个树是二叉搜索树”的充分必要条件。也就是说根据这个性质，二叉搜索树的最小值一定是从根节点开始一直往做儿子走的点；最大值同理。那么不难写出如下代码：

1
2
3
4
5
6
7
8
9
10
// 由于直接返回了指针，所以先认为不会是空节点
// 这个两个函数的含义都是求以 p 为根的子树的极值
inline TreeNode *findMin(TreeNode *p) {
    while(p->ls != nullptr) p = p->ls;
    return p;
}
inline TreeNode *findMax(TreeNode *p) {
    while(p->rs != nullptr) p = p->rs;
    return p;
}

插入元素

插入元素和元素搜索一个原理，如果找不到就新建点，重复了就增加一开始的重复元素变量。

1
2
3
4
5
6
7
8
TreeNode  *insert(TreeNode *p, int x) {
   	if(p == nullptr) return new TreeNode(x);
    if(x < p->val) p->ls = insert(root->ls, x);
    else if(x > p->val) p->rs = insert(p->rs, x);
    else p->cnt++;
    p->sz = p->cnt + (root->ls ? root->ls->sz : 0) + (root->rs ? root->rs->sz : 0);
	return p;
}

删除元素

删除元素的细节就比较多了。我们来考虑删除一个点有多少种情况：

  1. 要求删除的是一个不存在的点，忽略操作
  2. 删除点的 cnt 大于 $1$，即有重复点，直接减少 cnt 即可。
  3. 删除点的 cnt 等于 $1$，即没有重复点，这时候情况复杂，需要分类讨论。

没有重复点，那么这个点就需要被移除，而这样移除的操作就需要修改问题的一系列点，那么不难想到也把删除函数的返回值设置为指针类型，这样方便书写。

回到分讨的问题上来，删除一个点会有三种情况：

  1. 这个点没有左子树，那么显然直接把右子树接到这个位置上即可
  2. 这个点没有右子树，同理。
  3. 这个点左右两个子树都有。那么这时候如何修改呢？介于二叉搜索树的性质，右子树的最小值一定比左子树的最大值大，所以我们有两种修改方式：
    • 把左子树的最大值作为新的根节点，然后把当新的根节点的左子树变为删去最大值以后的原来左子树即可。
    • 右子树同理。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
TreeNode *erase(TreeNode *p, int x) {
    if(p == nullptr) return p; // 空指针，直接忽略
	if(x < p->val) p->ls = erase(p->ls, x);
    else if(x > p->val) p->rs = erase(p->rs, x);
    else if(p->cnt > 1) p->cnt--;
    else {
        if(p->ls == nullptr) {
            TreeNode* np = p->rs;
            delete p; // 释放内存
            return np; // 因为右子树直接接过来，没有任何要修改的内容，所以可以直接返回
        }
        else if(p->rs == nullptr) {
            TreeNode* np = p->ls;
            delete p;
            return np;
        }
        else {
            // 这里已经提前特判了左右子树空集的情况，所以直接调用了函数，当时函数里也没判断空指针
            TreeNode* np = findMin(p->rs);
			p->val = np->val, p->cnt = np->cnt;
            np->cnt = 1; // 保证后续递归时一遍删除就能删掉该点
            p->rs = erase(p->rs, np->val);
        }
    }
    // 重新处理一路上修改掉的其他信息
    p->sz = p->cnt + (root->ls ? root->ls->sz : 0) + (root->rs ? root->rs->sz : 0);
	return p;
}

计算排名

这个很简单，按照查询的顺序一路返回答案即可。

这里定义排名是树上每一个值排序后，相同元素中的第一个在排序后序列的位置（从一开始）

1
2
3
4
5
6
int queryRank(TreeNode *p, int x) {
    if(p == nullptr) return 0;
    if(p->val == x) return (p->ls ? p->ls->sz : 0) + 1;
    if(p->val > v) return queryRank(p->ls, x);
    return queryRank(p->rs, x) + (p->ls ? p->ls->sz : 0) + p->cnt;
}

定位查找

与计算元素的排名同理，一路反推回去即可。

1
2
3
4
5
6
7
8
9
int querykth(TreeNode *p int x) {
    if(p == nullptr) return -1; // 空指针特殊值
    if(p->ls) {
        if(p->ls->sz >= k) return querykth(p->ls, k);
        else if(p->ls->sz + p->cnt >= k) return p->val;
    }
    else if(k == 1) return p->val;
    return querykth(p->rs, k - (p->ls ? p->ls->sz : 0) - p->cnt);
}

特性剖析：还阳

仔细观察一下上面的函数，基本上全都是最坏情况下会从根一直走到叶子的。那么从根到叶子的距离，其实就是一棵树的高度，一般记作 $h$，那么上面的函数的时间复杂度全都是 $O(h)$，而这个 $h$ 的大小是多少呢？理想情况下，这棵二叉树接近一棵完整二叉树（即所有点的儿子数量不是 $0$ 个就是 $2$ 个）那么显然它的深度就是 $\log n$ 数量级的。也就是说，二叉搜索树的期望最优复杂度，应该是 $O(\log n)$，其中 $n$ 是节点数量。

但是这对吗？期望是期望，实际是实际。我们可以想一下对于一个 $n$ 节点的二叉树，其深度最坏是多少？没错，当树退化成一条链的时候，我们二叉搜索树的复杂度就退化成了 $O(n)$，完全无法接受。这时候我们要如何是好呢？

由于树高度的不平衡，一种新的数据结构应运而生，也就是我们常说的平衡树，如果一棵树的高度越接近 $\log n$，就说明这棵树具有越强的平衡性。平衡树就是可以通过一些操作来维持树的高度以降低复杂度的二叉搜索树。

基本上来说，最常用的平衡树也就两种：$\tt Treap$ 和 $\tt Splay$。本文的主要内容就是讲解 Treap 的两种类型：带旋 Treap 和无旋 Treap，我个人来说觉得无旋 Treap 更简单，所以就放在了前面，第二个讲带旋 Treap，预计不久之后也会发文讲一下 Splay 树。大概就是这样，接下来我们来看——无旋 Treap。

算法其一：三尘

基础概念：冥谶天笔

首先来说无旋 Treap。第一个要了解的概念是，为什么这个算法叫无旋 Treap。重点自然在“无旋”二字，这是因为一般来说，平衡树维持二叉搜索树平衡的方式是旋转，而无旋 Treap 维护高度的方式不是旋转，而是分裂与合并，这种特殊的操作就使得无旋 Treap 可以有修改区间和可持久化的能力（有空我也研究下qwq，已知名字叫 FHQ-Treap）

分裂与合并两个操作，其实很简单，字面意思就是把一个 Treap 分裂成两个 Treap；而合并就是把两个 Treap 合并成一个 Treap。（接下来介绍无旋 Treap 时候的 Treap 除特殊指出以外，全部都是无旋 Treap；介绍有旋 Treap 的时候同理）

另外还有一个 Treap 的特性，就是不论有旋还是无旋的 Treap 都有的性质。Treap 之所以叫 Treap 它的名字其实是两个数据结构的结合体：Tree+Heap，其中 Tree 特指二叉搜索树，Heap 表示堆。所以 Treap 也被叫做树堆，它上面的节点拥有两个关键字 val,key 。其中关键字 val 满足二叉搜索树的性质、key 满足堆的性质。

这样做原因，是因为如果没有 $\tt key$ 这个参数，就会导致顺序插入 $\tt val$ 的时候，树退化成一条链。而加入了 $\tt key$ 这个参数以后，由于要额外满足 $\tt key$ 成一个堆，所以就以堆是完全二叉树这样的性质锁住了 Treap 的高度（当然由于同时要满足是二叉搜索树，所以大多数时候 Treap 都不是完全二叉树，高度也会高于 $\log n$，这是一种弱平衡的平衡树）

而由于这个 $\tt key$ 是用来维持树的高度的，它可能不会参与操作，但是他的值至关重要。如果每一个插入的点的 $\tt key$ 是与插入顺序正相关的话，这棵树会严重失衡（可以自己举例试一下，不论你是维护小根堆 $\tt key$ 还是大根堆都是如此）如果与插入的 $\tt val$ 正相关的话，这棵树会直接退化成链。所以最好的方式就是随机生成键值 $\tt key$。

复杂度证明我不会，建议直接看 Treap - OI Wiki 。

思想模拟：生灭系缚

那么刚刚说过了，无旋 Treap 的主要维护平衡手段是分裂和合并，但不论是分裂还是合并，最终的结果一定是一个由若干 Treap 组成的森林。也就是分裂或者合并前后，都同时满足二叉搜索树及堆的性质。

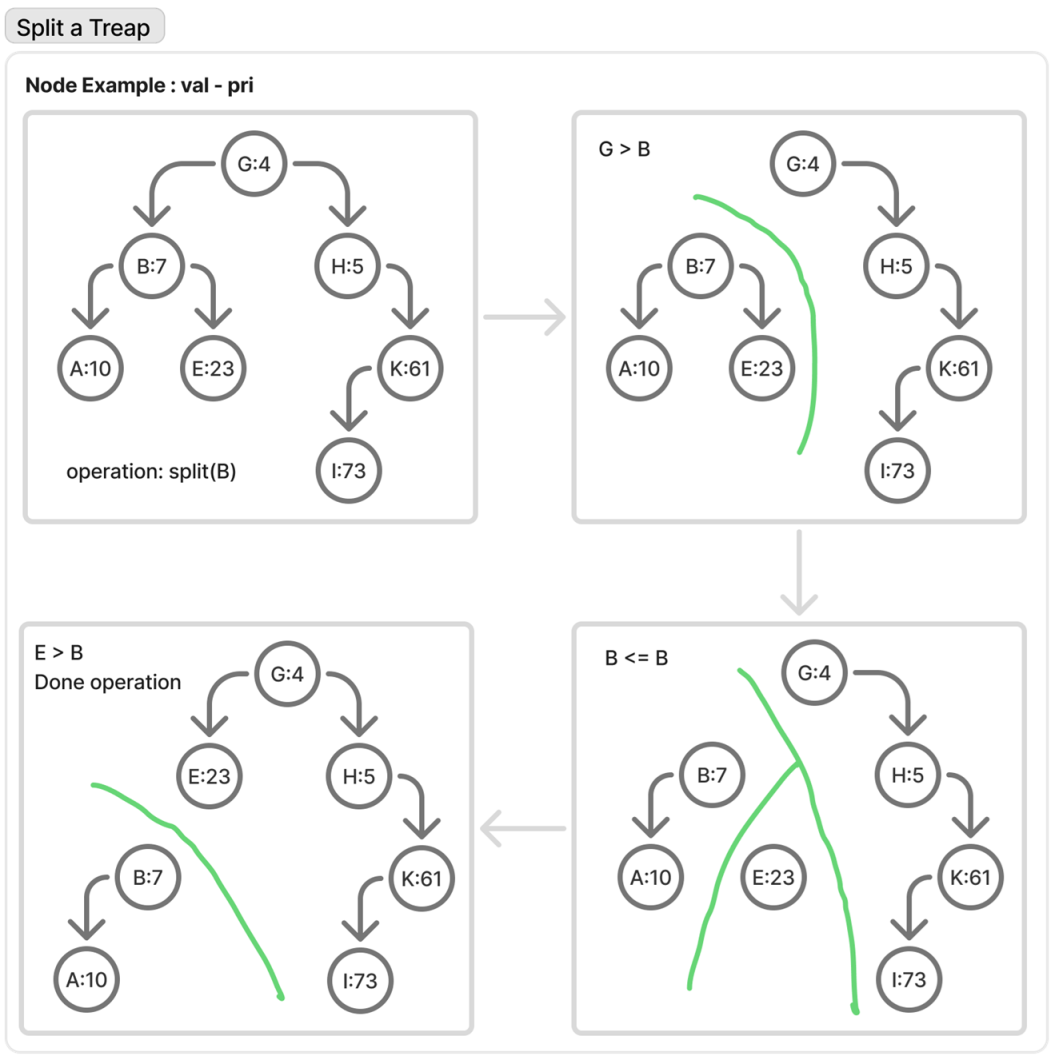
分裂

首先来看分裂。一般来说，无旋 Treap 的分裂都是按照数值分裂的。我们可以先随便给出一个 Treap 然后手动模拟一下分裂的过程来感受。

分裂操作示例

由于二叉搜索树的性质，当我们发现某一个点的权值要小（或者大）的时候，由于左子树全都小于根，右子树全部大于根，所以每次可以扔掉一个子树，这样理想情况下每次扔掉一半的点，复杂度即为 $O(\log n)$。

代码也就不难写了。这里说一下如何设计这个函数，由于分裂操作会导致一个 Treap 变为 两个 Treap，这就需要我们保存新的两个 Treap 的根节点，以方便合并操作。每一次会经过一个节点，辅助判断的信息只有我们需要分裂的键值，所以参数只需要根节点指针和分裂键值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
pair<Node *, Node *> split(Node *p, int x) {
    // 日常特判空指针
    if(cur == nullptr) return {nullptr, nullptr};
    if(p->val <= x) {
        // 左子树一定都小了，接下来处理右子树
        auto tmp = split(p->rs, x);
        p->rs = tmp.first; // 把右子树小于 x 的部分拼过来
        p->upd_siz(); // 更新子树大小
        return {p, tmp.second};
    }
    else {
        // 同理
        auto tmp = split(p->ls, x);
        p->ls = tmp.second;
        p->upd_siz();
        return {tmp.first, p};
    }
}

这样就是无旋 Treap 分裂的代码了，接下来是另外一个基本操作——合并。

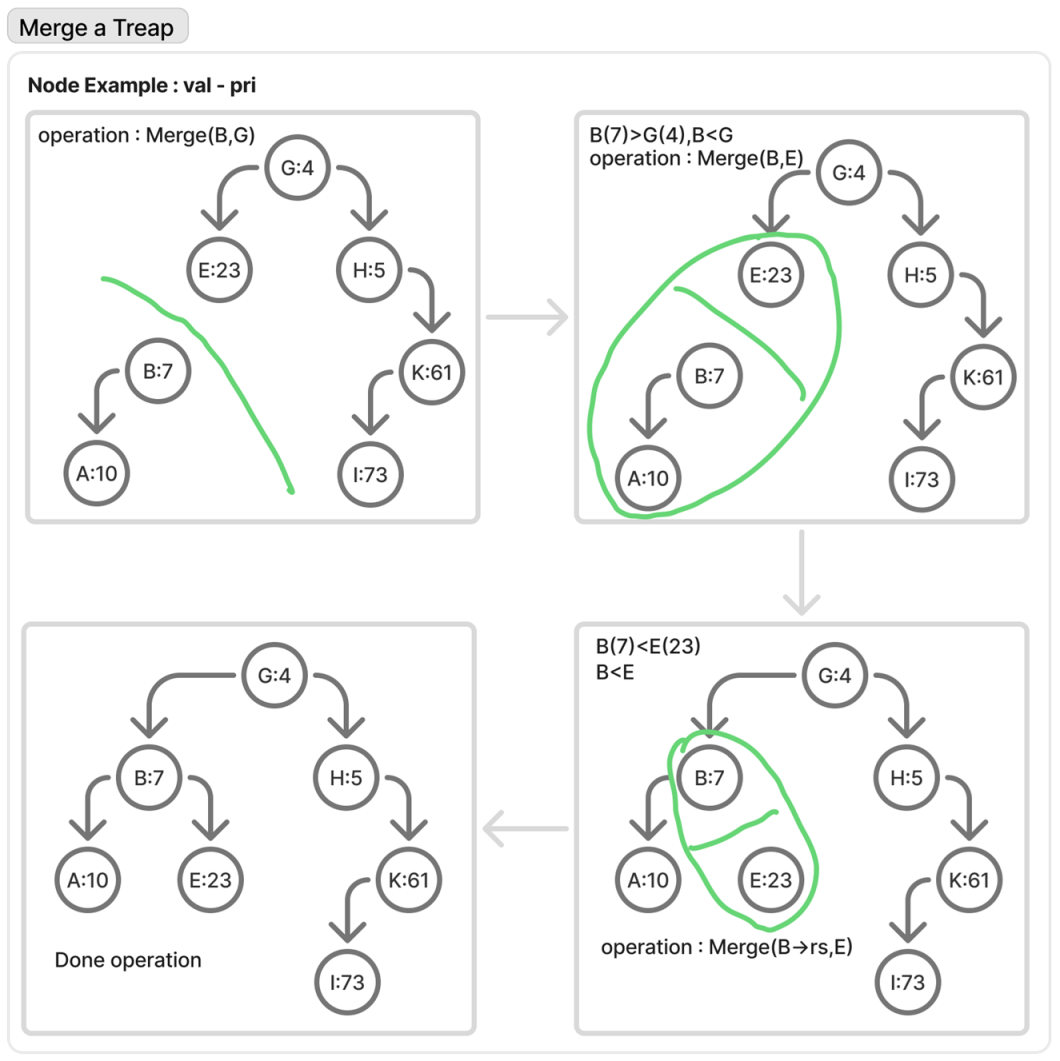
合并

合并其实是分裂的逆运算，由于分裂后的两个 Treap 都满足二叉搜索树性质，所以在分裂函数中主要维护的是堆键值的堆性质。同样我们可以把刚刚分裂开来的两个 Treap 合并一下，来验证合并是否是分裂逆运算。

合并操作示例

可以注意到确实合并回了原来的那颗 Treap。合并需要注意两个点，由于两边都是 Treap 所以有限考虑维护堆性质。堆只需要满足小堆键值在父亲方向即可。除此之外，知道了父亲和儿子的关系，接下来就可以开始考虑左右子树。左右子树的要求来自二叉搜索树的性质，因为二叉搜索树要求左子树全部小于根，右子树全部大于根。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 输入要合并的两个子树，返回新的根。
Node *merge(Node *u, Node *v) {
    // 空指针特判
    if(u == nullptr && v == nullptr) return nullptr;
    if(u == nullptr) return v;
    if(v == nullptr) return u;
    // 方便后续左右儿子的插入
    if(u.val > v.val) swap(u, v);
    // 维护堆，判断父亲
    if(u.pri < v.pri) {
        // 上面确立的 u 的所有维护值都小于 v
        // 根据二叉搜索树的性质，v 应该被并到右子树
        u.rs = merge(u.rs, v);
        u->upd_siz();
        return u;
    }
    else {
        // 同理
        v.ls = merge(u, v.ls);
        v->upd_siz();
        return v;
    }
}

插入

那么我们搞定了两个最大的操作，生下来全都是基于这两个操作的变种了。

最简单的莫过于插入和删除。试想一下，在一个存储了 $[l,r]$ 值的 Treap 中，我们要删除一个存在的 $x$，这时候如何使用分裂和合并操作是这个点消失呢？很简单，只要四步。

  1. $\tt auto\ now = Split(root, x);$
  2. $\tt auto\ tmp = Split(now.first, x - 1);$
  3. $\tt add\ tmp.second$
  4. $\tt root = merge(tmp.first, now.second);$

上面这段伪代码也不难理解。先按照 $x$ 的值把原树分裂，这里要注意的是，$x$ 不一定是在原来的 Treap 里面就被存储的，最终分裂结果一定是第一个 Treap $\le x$、第二个 Treap $\gt x$。然后我们就要把 $x$ 这个值的位置给预留出来。这里为什么第二个分裂不是也按照 $x$ 来分裂呢？当然也可以按照 $x$ 分裂，只不过 $x-1$ 分裂的话第二个 Treap 的根其实就是一个小于等于 $x$、大于 $x-1$ 的值，这个值只能有两种，$x$ 或者 NULL，这样的话对于我们来说非常的方便，所以选择了这样来分裂 Treap。

1
2
3
4
5
6
7
inline void insert(int x) {
    auto tmp = split(root, x);
    auto ltr = split(tmp.first, x - 1);
    if(ltr.second == nullptr) ltr.second = new Node(x);
    else ltr.second->cnt++, ltr.second->upd_siz();
    root = merge(merge(ltr.first, ltr.second), tmp.second);
}

删除

删除是和插入同理的操作，这两个也是一组互逆运算，就不再赘述了。

1
2
3
4
5
6
7
inline void erase(int x) {
    auto tmp = split(root, x);
    auto ltr = split(tmp.first, x - 1);
    if(ltr.second->cnt > 1) ltr.second->cnt--, ltr.second->upd_siz();
    else delete ltr.second, ltr.second = nullptr;
    root = merge(merge(ltr.first, ltr.second), tmp.second);
}

排名

排名也很简单，我们知道每一个数值的定义，其实就是比它小的数的数量再加一。还是一样，如果我们按照要查询的数 $x$ 分裂 $x-1$，那么第一个子树的内容，就是所有小于 $x$ 的点，这样就可以查询出排名。

1
2
3
4
5
6
inline int qrank(Node *p, int x) {
    auto tmp = split(p, x - 1);
    int ans = (tmp.first == nullptr ? 0 : tmp.first->sz) + 1;
    p = merge(tmp.first, tmp.second); // 最后
    return ans;
}

顺带一提，这一部分OI-wiki上是有误的，我发现的……

位值

另外一个部分就是根据排名查询值。根据排名与根据数值是不一样的，因为数值我们可以轻松的判断出大小，但排名不同。虽然二叉搜索树有左右子树大小关系的性质，我们确实可以递归来得到排名第几的点是什么。但是更广泛的，如果我们要查询一个数的前驱或者后继，这时候用排名分裂 Treap 会显得更加有效。

那么我们来思考一下如何用排名分裂 Treap。其实也和按照数值分裂差不多。只不过判断的依据变成了左子树的大小，直接放代码了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pair<Node *, Node *>split_rk(Node *p, int rk) {
    if(p == nullptr) return {nullptr, nullptr};
	int siz = p->ls ? p->ls->sz : 0;
	if(rk <= siz) {
        auto tmp = split_rk(p->ls, rk);
        p->ls = tmp.second;
        p->upd_siz();
        return {tmp.first, p};
    }
    else {
        auto tmp = split_rk(p->rs, rk - siz - 1);
        p->rs = tmp.first;
        p->upd_siz();
        return {p, tmp.second};
    }
}

那么有了这个东西，位置查询值也就呼之欲出了。

1
2
3
4
5
6
7
inline int qval(Node *p, int rk) {
    auto tmp = split_rk(p, rk);
    auto ltr = split_rk(tmp.first, rk - 1);
    int ans = ltr.second->val;
    p = merge(merge(ltr.first, ltr.second), tmp.second);
    return ans;
}

算法拓展：十王赦令

那么在最开始就说过，无旋 Treap 天生有处理区间问题的优势，所以我们来看看 Treap 如何应用于区间修改问题。

区间操作思想

显然的，一棵树的中序遍历可以看作一个区间，如果我们对于 Treap 进行中序遍历，它所得到一定是一个递增的序列。如果对于这个序列进行改动，也就是更改 Treap 的形态，也可以达到修改区间的目的。

但是我们直接修改 Treap 形态是不现实的。Treap 既要维护二叉搜索树性质，又要维护堆性质，这使得直接修改 Treap 的形态会使 Treap 丧失两种性质。事实上确实如此，我们只维护堆性质，放弃二叉搜索树性质。但这也使得分裂不再可以以数值分裂，而是只能以排名（甚至不是排名，应该说是该节点在中序遍历中的位置）来分裂了。

合并同样需要改动，由于不再需要维护二叉搜索树性质，左右子树便没有判断大小的需要了。

区间操作实现

接下来解析一下一些区间操作。第一个还是把分裂与合并先掏出来，分裂与合并的区别我们都讲过了。但是除此之外，还有一个重要的变化，无旋 Treap 支持区间操作以后，其实更加倾向于一个线段树的加强版。他也会有自己每个节点要维护的信息，而且同样的，为了节省时间复杂度，他也有懒标记，所以其实还多了 pushdown 和 pushup 这类的维护树上信息正确性的函数。

关于这些函数，灵活性较高，所以不放在这里模板代码解释了，如果还有线段树的区间操作不会的，可以去看看我的博文，我写线段树的文章还挺多的。

友情链接：

标签: 线段树 | 祝馀宫

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
pair<Node*, Node*> split(Node* cur, int sz) {
    // 按照树的大小划分
    if (cur == nullptr) return { nullptr, nullptr };
    cur->check_tag();
    if (sz <= siz(cur->ch[0])) {
        // 左边的子树就够了
        auto temp = split(cur->ch[0], sz);
        // 左边的子树不一定全部需要，temp.second 是不需要的
        cur->ch[0] = temp.second;
        cur->upd_siz();
        return { temp.first, cur };
    }
    else {
        // 左边的加上右边的一部分（当然也包括这个节点本身）
        auto temp = split(cur->ch[1], sz - siz(cur->ch[0]) - 1);
        cur->ch[1] = temp.first;
        cur->upd_siz();
        return { cur, temp.second };
    }
}

Node* merge(Node* sm, Node* bg) {
    // small, big
    if (sm == nullptr && bg == nullptr) return nullptr;
    if (sm != nullptr && bg == nullptr) return sm;
    if (sm == nullptr && bg != nullptr) return bg;
    sm->check_tag(), bg->check_tag();
    if (sm->prio < bg->prio) {
        sm->ch[1] = merge(sm->ch[1], bg);
        sm->upd_siz();
        return sm;
    }
    else {
        bg->ch[0] = merge(sm, bg->ch[0]);
        bg->upd_siz();
        return bg;
    }
}

这下全都是按照区间的表示方法来的了，也就是说比如我要从 Treap 中分裂出一个区间 $[l,r]$ 很简单只需要调用分裂函数两次 ：Split(l-1) 和 Split(r - l + 1)，这个的意思是先把前 $l-1$ 个数去掉，再在剩下的序列里面取出前序列长度个数字，这样做法的优点据说是如果 $r$ 超出了数的范围，它不会报错（好吧无法理解）

然后其实就都挺常规了，自己理解理解其实是可以做的。

实现综合：遍土遵行

这里主要是放两道例题。

普通无旋 Treap

P3369 【模板】普通平衡树 - 洛谷

这个其实就是最基础的 Treap，但是众所周知上面的代码全都是来自 OI Wiki，这玩意实在是太抽象了，所以这里放上我自己觉得挺不错的普通无旋 Treap 的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

struct Node {
    ll val, pri;
    ll cnt, sz;
    Node *ls, *rs;
    Node(ll x) : val(x), pri(rand()), cnt(1), sz(1), ls(nullptr), rs(nullptr) {}
};

class fhq_Treap {
private:
    Node *root;

    inline void upd(Node* p) {
        p->sz = p->cnt + (p->ls ? p->ls->sz : 0) + (p->rs ? p->rs->sz : 0);
    }

    void split(Node* p, ll x, Node*& left, Node*& right) {
        if (!p) { left = right = nullptr; return; }
        if (p->val < x) {
            left = p;
            split(p->rs, x, left->rs, right);
            upd(left);
        } else {
            right = p;
            split(p->ls, x, left, right->ls);
            upd(right);
        }
    }

    Node* merge(Node* a, Node* b) {
        if (!a || !b) return a ? a : b;
        if (a->pri > b->pri) {
            a->rs = merge(a->rs, b);
            upd(a);
            return a;
        } else {
            b->ls = merge(a, b->ls);
            upd(b);
            return b;
        }
    }

public:
    fhq_Treap() : root(nullptr) {}

    void insert(ll x) {
        Node *left, *right, *mid, *tmp;
        split(root, x, left, tmp);
        split(tmp, x + 1, mid, right);
        if (mid) {
            mid->cnt++;
            upd(mid);
        } else {
            mid = new Node(x);
        }
        root = merge(merge(left, mid), right);
    }

    void erase(ll x) {
        Node *left, *right, *mid, *tmp;
        split(root, x, left, tmp);
        split(tmp, x + 1, mid, right);
        if (mid) {
            if (mid->cnt > 1) {
                mid->cnt--;
                upd(mid);
            } else {
                delete mid;
                mid = nullptr;
            }
        }
        root = merge(merge(left, mid), right);
    }

    ll qrank(ll x) {
        Node *left, *right;
        split(root, x, left, right);
        ll res = (left ? left->sz : 0) + 1;
        root = merge(left, right);
        return res;
    }

    ll qval(ll k) {
        Node* p = root;
        while (p) {
            ll lsz = p->ls ? p->ls->sz : 0;
            if (k <= lsz) {
                p = p->ls;
            } else if (k > lsz + p->cnt) {
                k -= lsz + p->cnt;
                p = p->rs;
            } else {
                return p->val;
            }
        }
        return -1;
    }

    ll qpre(ll x) {
        Node *left, *right;
        split(root, x, left, right);
        Node* p = left;
        if (!p) {
            root = merge(left, right);
            return -1;
        }
        while (p->rs) p = p->rs;
        ll res = p->val;
        root = merge(left, right);
        return res;
    }

    ll qnxt(ll x) {
        Node *left, *right;
        split(root, x + 1, left, right);
        Node* p = right;
        if (!p) {
            root = merge(left, right);
            return -1;
        }
        while (p->ls) p = p->ls;
        ll res = p->val;
        root = merge(left, right);
        return res;
    }
};

const int N = 1e5 + 5;

int n;

inline void Input() {
    read(n);
}

fhq_Treap treap;

inline void Work() {
    int op, x;
    while(n--) {
        read(op, x);
        if(op == 1) treap.insert(x);
        else if(op == 2) treap.erase(x);
        else if(op == 3) printf("%d\n", treap.qrank(x));
        else if(op == 4) printf("%d\n", treap.qval(x));
        else if(op == 5) printf("%d\n", treap.qpre(x));
        else if(op == 6) printf("%d\n", treap.qnxt(x));
    }
}

int main() {
    srand(time(0));
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

区间无旋 Treap

这有一道关于区间无旋 Treap 的超级史山题：266. 超级备忘录 - AcWing题库

能过的都是属于 FHQ-Treap 大蛇了（

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const ll inf = 4557430888798830399;
const ll N = 200010;

ll n, m;
ll ch[N][2], val[N], key[N], idx;
ll sz[N], mn[N];
ll add[N], rev[N];
ll root;

ll newNode(ll v) {
    val[++idx] = v;
    key[idx] = rand();
    sz[idx] = 1;
    mn[idx] = val[idx];
    return idx;
}

void pushUp(ll u) {
    sz[u] = sz[ch[u][0]] + sz[ch[u][1]] + 1;
    mn[u] = min(val[u], min(mn[ch[u][0]], mn[ch[u][1]]));
}

void pushAdd(ll u, ll k) {
    val[u] += k;
    mn[u] += k;
    add[u] += k;
}

void pushRev(ll u) {
    swap(ch[u][0], ch[u][1]);
    rev[u] ^= 1;
}

void pushDown(ll u) {
    if (add[u]) {
        pushAdd(ch[u][0], add[u]);
        pushAdd(ch[u][1], add[u]);
        add[u] = 0;
    }
    if (rev[u]) {
        pushRev(ch[u][0]);
        pushRev(ch[u][1]);
        rev[u] = 0;
    }
}

void split(ll u, ll &x, ll &y, ll k) {
    if (!u) {
        x = y = 0;
        return;
    }
    pushDown(u);
    if (sz[ch[u][0]] + 1 <= k) {
        x = u;
        split(ch[u][1], ch[x][1], y, k - sz[ch[u][0]] - 1);
        pushUp(x);
    } else {
        y = u;
        split(ch[u][0], x, ch[y][0], k);
        pushUp(y);
    }
}

ll merge(ll x, ll y) {
    if (!x || !y) return x + y;
    pushDown(x);
    pushDown(y);
    if (key[x] <= key[y]) {
        ch[x][1] = merge(ch[x][1], y);
        pushUp(x);
        return x;
    } else {
        ch[y][0] = merge(x, ch[y][0]);
        pushUp(y);
        return y;
    }
}

void insert(ll pos, ll v) {
    ll x, y;
    split(root, x, y, pos);
    root = merge(merge(x, newNode(v)), y);
}

void deleteNode(ll pos) {
    ll x, y, z;
    split(root, y, z, pos);
    split(y, x, y, pos - 1);
    root = merge(x, z);
}

void updateAdd(ll l, ll r, ll k) {
    ll x, y, z;
    split(root, x, y, l - 1);
    split(y, y, z, r - l + 1);
    pushAdd(y, k);
    root = merge(x, merge(y, z));
}

void updateRev(ll l, ll r) {
    ll x, y, z;
    split(root, x, y, l - 1);
    split(y, y, z, r - l + 1);
    pushRev(y);
    root = merge(x, merge(y, z));
}

void updateShift(ll l, ll r, ll n) {
    ll len = r - l + 1 - n % (r - l + 1);
    ll x, y, z, p;
    split(root, x, y, l - 1);
    split(y, y, z, len);
    split(z, z, p, r - l + 1 - len);
    root = merge(merge(merge(x, z), y), p);
}

ll queryMin(ll l, ll r) {
    ll x, y, z;
    split(root, x, y, l - 1);
    split(y, y, z, r - l + 1);
    ll res = mn[y];
    root = merge(x, merge(y, z));
    return res;
}

int main() {
    srand(time(0));
    val[0] = mn[0] = inf;
    scanf("%lld", &n);
    for (ll i = 1; i <= n; i++) {
        ll x;
        scanf("%lld", &x);
        root = merge(root, newNode(x));
    }
    scanf("%lld", &m);
    while (m--) {
        char op[10];
        ll x, y, k;
        scanf("%s", op);
        if (op[0] == 'A') {
            scanf("%lld%lld%lld", &x, &y, &k);
            updateAdd(x, y, k);
        } else if (op[0] == 'I') {
            scanf("%lld%lld", &x, &k);
            insert(x, k);
        } else if (op[0] == 'D') {
            scanf("%lld", &x);
            deleteNode(x);
        } else if (op[0] == 'M') {
            scanf("%lld%lld", &x, &y);
            printf("%lld\n", queryMin(x, y));
        } else if (op[3] == 'E') {
            scanf("%lld%lld", &x, &y);
            updateRev(x, y);
        } else {
            scanf("%lld%lld%lld", &x, &y, &k);
            updateShift(x, y, k);
        }
    }
    return 0;
}

算法其二：四谛

思想简介：幽府判罚

带旋 Treap 可能相对来说会复杂一点，但不多。带旋 Treap 之所以叫做带旋，是因为它维护平衡性的操作是旋转。那么什么是旋转操作呢？

首先给出旋转操作的定义：在不影响二叉搜索树性质的情况下，把原来的左子树变为根节点（或者把原来的右子树变成根节点）然后取名变成更节点的子树相反方向的旋转名称（比如说左子树变根就是右旋）

这个操作的意义在于，旋转可以修改原来的树的高度，这样就使得复杂度变得正确。

分段实现：命尔臂助

同样的我们一段一段来完成有旋 Treap 的代码编写。

节点结构

不多说，和无旋 Treap 基本没有 区别，唯一的区别是为了方便旋转操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
struct Node {
  Node *ch[2];  // 两个子节点的地址
  int val, rank;
  int rep_cnt;  // 当前这个值（val）重复出现的次数
  int siz;      // 以当前节点为根的子树大小

  Node(int val) : val(val), rep_cnt(1), siz(1) {
    ch[0] = ch[1] = nullptr;
    rank = rand();
    // 注意初始化的时候，rank 是随机给出的
  }

  void upd_siz() {
    // 用于旋转和删除过后，重新计算 siz 的值
    siz = rep_cnt;
    if (ch[0] != nullptr) siz += ch[0]->siz;
    if (ch[1] != nullptr) siz += ch[1]->siz;
  }
};

子树旋转

模拟刚刚的意思即可。这里放上一张 OI-wiki 的图片，清晰的讲述了旋转操作的过程。

旋转操作

不难注意到旋转操作不会影响中序遍历，即二叉搜索树的性质，主要是用来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void _rotate(Node *&cur, int dir) {  // dir参数代表旋转的方向 0为右旋，1为左旋
  // 注意传进来的 cur 是指针的引用，也就是改了这个
  // cur，变量是跟着一起改的，如果这个 cur 是别的 树的子节点，根据 ch
  // 找过来的时候，也是会找到这里的

  // 以下的代码解释的均是左旋时的情况
  Node *tmp = cur->ch[dir];  // 让 C 变成根节点，
                             // 这里的 tmp
                             // 是一个临时的节点指针，指向成为新的根节点的节点

  /* 左旋：也就是让右子节点变成根节点
   *         A                 C
   *        / \               / \
   *       B  C    ---->     A   E
   *         / \            / \
   *        D   E          B   D
   */
  cur->ch[dir] = tmp->ch[!dir];    // 让 A 的右子节点变成 D
  tmp->ch[!dir] = cur;             // 让 C 的左子节点变成 A
  cur->upd_siz(), tmp->upd_siz();  // 更新大小信息
  cur = tmp;  // 最后把临时储存 C 树的变量赋值到当前根节点上（注意 cur 是引用）
}

数值插入

插入一个数也很简单，我们先按照二叉搜索树的性质，找到这个点应该存在的位置，然后用旋转操作维护堆键值就可以了（是因为学完无旋 Treap 的原因吗，怎么莫名感觉简单的没话说

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void _insert(Node *&cur, int val) {
  if (cur == nullptr) {
    // 没这个节点直接新建
    cur = new Node(val);
    return;
  } else if (val == cur->val) {
    // 如果有这个值相同的节点，就把重复数量加一
    cur->rep_cnt++;
    cur->siz++;
  } else if (val < cur->val) {
    // 维护搜索树性质，val 比当前节点小就插到左边，反之亦然
    _insert(cur->ch[0], val);
    if (cur->ch[0]->rank < cur->rank) {
      // 小根堆中，上面节点的优先级一定更小
      // 因为新插的左子节点比父节点小，现在需要让左子节点变成父节点
      _rotate(cur, RT);  // 注意前面的旋转性质，要把左子节点转上来，需要右旋
    }
    cur->upd_siz();  // 插入之后大小会变化，需要更新
  } else {
    _insert(cur->ch[1], val);
    if (cur->ch[1]->rank < cur->rank) {
      _rotate(cur, LF);
    }
    cur->upd_siz();
  }
}

数值删除

数值删除就略微有一些复杂，我们要分类讨论这个删除的点的左右子树情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
void _del(Node *&cur, int val) {
  if (val > cur->val) {
    _del(cur->ch[1], val);
    // 值更大就在右子树，反之亦然
    cur->upd_siz();
  } else if (val < cur->val) {
    _del(cur->ch[0], val);
    cur->upd_siz();
  } else {
    if (cur->rep_cnt > 1) {
      // 如果要删除的节点是重复的，可以直接把重复值减小
      cur->rep_cnt--, cur->siz--;
      return;
    }
    uint8_t state = 0;
    state |= (cur->ch[0] != nullptr);
    state |= ((cur->ch[1] != nullptr) << 1);
    // 00都无，01有左无右，10，无左有右，11都有
    Node *tmp = cur;
    switch (state) {
      case 0:
        delete cur;
        cur = nullptr;
        // 没有任何子节点，就直接把这个节点删了
        break;
      case 1:  // 有左无右
        cur = tmp->ch[0];
        // 把根变成左儿子，然后把原来的根节删了，注意这里的 tmp 是从 cur
        // 复制的，而 cur 是引用
        delete tmp;
        break;
      case 2:  // 有右无左
        cur = tmp->ch[1];
        delete tmp;
        break;
      case 3:
        int dir = cur->ch[0]->rank < cur->ch[1]->rank
                           ? 0
                           : 1;  // dir 是 rank 更小的那个儿子
        _rotate(cur, dir);  // 这里的旋转可以把优先级更小的儿子转上去，rt 是 0，
                            // 而 lf 是 1，刚好跟实际的子树下标反过来
        _del(
            cur->ch[!dir],
            val);  // 旋转完成后原来的根节点就在旋方向那边，所以需要
                   // 继续把这个原来的根节点删掉
                   // 如果说要删的这个节点是在整个树的「上层的」，那我们会一直通过这
                   // 这里的旋转操作，把它转到没有子树了（或者只有一个），再删掉它。
        cur->upd_siz();
        // 删除会造成大小改变
        break;
    }
  }
}

排名查询

这个简单，同理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int _query_rank(Node *cur, int val) {
  int less_siz = cur->ch[0] == nullptr ? 0 : cur->ch[0]->siz;
  // 这个树中小于 val 的节点的数量
  if (val == cur->val)
    // 如果这个节点就是要查的节点
    return less_siz + 1;
  else if (val < cur->val) {
    if (cur->ch[0] != nullptr)
      return _query_rank(cur->ch[0], val);
    else
      return 1;  // 如果左子树是空的，说比最小的节点还要小，那这个数字就是最小的
  } else {
    if (cur->ch[1] != nullptr)
      // 如果要查的值比这个节点大，那这个节点的左子树以及这个节点自身肯定都比要查的值小
      // 所以要加上这两个值，再加上往右边找的结果
      // （以右子树为根的子树中，val 这个值的大小的排名）
      return less_siz + cur->rep_cnt + _query_rank(cur->ch[1], val);
    else
      return cur->siz + 1;
    // 没有右子树的话直接整个树 + 1 相当于 less_siz + cur->rep_cnt + 1
  }
}

定位询问

这个也是同理……

1
2
3
4
5
6
7
8
9
10
11
int _query_val(Node *cur, int rank) {
  // 查询树中第 rank 大的节点的值
  int less_siz = cur->ch[0] == nullptr ? 0 : cur->ch[0]->siz;
  // less siz 是左子树的大小
  if (rank <= less_siz)
    return _query_val(cur->ch[0], rank);
  else if (rank <= less_siz + cur->rep_cnt)
    return cur->val;
  else
    return _query_val(cur->ch[1], rank - less_siz - cur->rep_cnt);  // 见前文
}

代码一览：在此成书

同样，还是以 P3369 为例，把 OI-wiki 的抽象代码人类化一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar()(p1 == p2 &&(p2 =(p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while(!isdigit(ch = getchar())) if(ch == '-') f = -1;
        while(isdigit(ch)) x =(x << 1) +(x << 3) +(ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

struct Node {
    Node* ch[2];
    int val, pri;
    int cnt, siz;
    Node(int val) : val(val), cnt(1), siz(1) {
        ch[0] = ch[1] = nullptr;
        pri = rand();
    }
    void upd_siz() {
        siz = cnt;
        if(ch[0] != nullptr) siz += ch[0]->siz;
        if(ch[1] != nullptr) siz += ch[1]->siz;
    }
};
class Treap {
private:
    Node* root;
    int q_prev_tmp = 0, q_nex_tmp = 0;
    void _rotate(Node*& p, int dir) {
        Node* tmp = p->ch[dir];
        p->ch[dir] = tmp->ch[!dir];
        tmp->ch[!dir] = p;
        p->upd_siz(), tmp->upd_siz();
        p = tmp;
    }
    void _insert(Node*& p, int val) {
        if(!p) { p = new Node(val);return; }
        else if(val == p->val) p->cnt++, p->siz++;
        else if(val < p->val) {
            _insert(p->ch[0], val);
            if(p->ch[0]->pri < p->pri) _rotate(p, 0);
            p->upd_siz();
        }
        else {
            _insert(p->ch[1], val);
            if(p->ch[1]->pri < p->pri) _rotate(p, 1);
            p->upd_siz();
        }
    }
    void _del(Node*& p, int val) {
        if(val > p->val) _del(p->ch[1], val), p->upd_siz();
        else if(val < p->val) _del(p->ch[0], val), p->upd_siz();
        else {
            if(p->cnt > 1) {
                p->cnt--, p->siz--;
                return;
            }
            Node* tmp = p;
            if(!p->ch[0] && !p->ch[1]) {
                delete p;
                p = nullptr;
                return;
            }
            else if(!p->ch[0]) {
                p = tmp->ch[1];
                delete tmp;
            }
            else if(!p->ch[1]) {
                p = tmp->ch[0];
                delete tmp;
            }
            else {
                int dir = p->ch[0]->pri < p->ch[1]->pri ? 0 : 1;
                _rotate(p, dir);
                _del(p->ch[!dir], val);
                p->upd_siz();
            }
        }
    }
    int _query_rank(Node* p, int val) {
        if(p == nullptr) return 0;
        int less_siz = p->ch[0] == nullptr ? 0 : p->ch[0]->siz;
        if(val == p->val) return less_siz + 1;
        else if(val < p->val) {
            if(p->ch[0] != nullptr) return _query_rank(p->ch[0], val);
            else return 1;
        }
        else {
            if(p->ch[1] != nullptr) 
                return less_siz + p->cnt + _query_rank(p->ch[1], val);
            else return p->siz + 1;
        }
    }
    int _query_val(Node* p, int rank) {
        int less_siz = p->ch[0] == nullptr ? 0 : p->ch[0]->siz;
        if(rank <= less_siz) return _query_val(p->ch[0], rank);
        else if(rank <= less_siz + p->cnt) return p->val;
        else return _query_val(p->ch[1], rank - less_siz - p->cnt);
    }
    int _query_prev(Node* p, int val) {
        if(val <= p->val) {
            if(p->ch[0] != nullptr) 
                return _query_prev(p->ch[0], val);
        }
        else {
            q_prev_tmp = p->val;
            if(p->ch[1] != nullptr) _query_prev(p->ch[1], val);
            return q_prev_tmp;
        }
        return -1;
    }
    int _query_nex(Node* p, int val) {
        if(val >= p->val) {
            if(p->ch[1] != nullptr) 
                return _query_nex(p->ch[1], val);
        }
        else {
            q_nex_tmp = p->val;
            if(p->ch[0] != nullptr) _query_nex(p->ch[0], val);
            return q_nex_tmp;
        }
        return -1;
    }
public:
    void insert(int val) { _insert(root, val); }
    void erase(int val) { _del(root, val); }
    int qrank(int val) { return _query_rank(root, val); }
    int qval(int rank) { return _query_val(root, rank); }
    int qpre(int val) { return _query_prev(root, val); }
    int qnxt(int val) { return _query_nex(root, val); }
};

const int N = 1e5 + 5;

int n;

inline void Input() {
    read(n);
}

Treap treap;

inline void Work() {
    int op, x;
    while(n--) {
        read(op, x);
        if(op == 1) treap.insert(x);
        else if(op == 2) treap.erase(x);
        else if(op == 3) printf("%d\n", treap.qrank(x));
        else if(op == 4) printf("%d\n", treap.qval(x));
        else if(op == 5) printf("%d\n", treap.qpre(x));
        else if(op == 6) printf("%d\n", treap.qnxt(x));
    }
}

int main() {
    srand(time(0));
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

细节对比：五阴

  • 两类 Treap 对比分析

就我写的这两份 Treap 代码而言，直观的区别有下。

有旋 Treap 无旋 Treap
代码长度 长 短
代码速度 短 长
代码空间 少 多
支持操作 少 多
可持久化 否 是

这个表格就是两类 Treap 的主要区别，可以按照标准来选择自己要使用哪种 Treap。

算法实战：六正

查看相关算法标签喵！

参考资料（以下排名不分先后）