理论:如何设计
需求:要解决的问题
对于一些题目,他们要求你计算一个区间内的最小值,没有操作,但是询问次数特别多,以至于树状数组和线段树 $O(m\log n)$ 的时间复杂度已经不够优秀,我们需要引入新的数据结构。
构造:寻找合理方案
同样的,我们说过,数据结构是时空平衡的,想要把单次询问复杂度降下来,就需要更高的预处理和空间复杂度。根据我们数据结构的根本是分组的思想,我们需要重新修改分组。
我们思考一下,理想状态是什么?理想状态是我们预处理出来的值可以直接拿出来用,或者经过 $1$ 次运算可以得出。
我们可以和两个极端比较一下。
| 预处理 | 单次 | |
|---|---|---|
| 数组 | 读入 $O(n)$ | for 一遍 $O(n)$ |
| 预处理出所有区间最值 | $O(n^2)$ | $O(1)$ |
| 理想数据结构 | 不知道 | 由于查询次数极多,所以必须需要单次 $O(1)$ 的算法 |
首先我们坑定得是 $1$ 对多的分组方式,我们可以打表看看
对于序列 $a[10] = [ 1, 4, 7, 3, 2, 8, 5, 9, 6, 10 ]$ 可以得出如下表格。
| 区间 $[l,r]$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 4 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | |
| 3 | 7 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | ||
| 4 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | |||
| 5 | 2 | 2 | 2 | 2 | 2 | 2 | ||||
| 6 | 8 | 5 | 5 | 5 | 5 | |||||
| 7 | 5 | 5 | 5 | 5 | ||||||
| 8 | 9 | 6 | 6 | |||||||
| 9 | 6 | 6 | ||||||||
| 10 | 10 |
首先,作为最基础的,每一个节点的单独值,都是要的。考虑 $[1, 2]$ 要不要,发现 $[1,2]$ 可以由 $[1, 1]$ 和 $[2, 2]$ 拼出来,但是如果不带的话,$[1, 3]$ 就不能 $1$ 次实现,所以 $[1, 2]$ 要带,同理,形如 $[l, l+1]$ 的区间都要带。可得下表:(加粗表示要带)
| 区间 $[l,r]$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :—————: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :——: |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | | 4 | 4 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | | | 7 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | | | | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 5 | | | | | 2 | 2 | 2 | 2 | 2 | 2 |
| 6 | | | | | | 8 | 5 | 5 | 5 | 5 |
| 7 | | | | | | | 5 | 5 | 5 | 5 |
| 8 | | | | | | | | 9 | 6 | 6 |
| 9 | | | | | | | | | 6 | 6 |
| 10 | | | | | | | | | | 10 |
同样的,考虑 $[1, 3]$ 要不要带,它可以被拼出来,而且如果不带,$[1, 4]$ 也可以一次拼出来,所以不用。而 $[1,4]$ 如果不带,$[1, 5]$ 就拼不出来。所以 $[1,3]$ 不带,$[1,4]$ 带。同理,形如 $[l, l+ 3]$ 的,都要带。
| 区间 $[l,r]$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :—————: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :——: |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | | 4 | 4 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | | | 7 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | | | | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 5 | | | | | 2 | 2 | 2 | 2 | 2 | 2 |
| 6 | | | | | | 8 | 5 | 5 | 5 | 5 |
| 7 | | | | | | | 5 | 5 | 5 | 5 |
| 8 | | | | | | | | 9 | 6 | 6 |
| 9 | | | | | | | | | 6 | 6 |
| 10 | | | | | | | | | | 10 |
以此类推,下一个要带的就是形如 $[l, l + 7]$ 的了,如下表
| 区间 $[l,r]$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :—————: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :—-: | :——: |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | | 4 | 4 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | | | 7 | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 4 | | | | 3 | 2 | 2 | 2 | 2 | 2 | 2 |
| 5 | | | | | 2 | 2 | 2 | 2 | 2 | 2 |
| 6 | | | | | | 8 | 5 | 5 | 5 | 5 |
| 7 | | | | | | | 5 | 5 | 5 | 5 |
| 8 | | | | | | | | 9 | 6 | 6 |
| 9 | | | | | | | | | 6 | 6 |
| 10 | | | | | | | | | | 10 |
观察刚刚的要的区间:$[l, l + 2^1 -1],[l, l+2^2 -1],[l,l+2^3-1]$ 。分组就显然了。
按照下标分组,将他的 $2^n$ 次幂分一组。
总结:何为倍增算法
倍增法(英语:$\tt binary\ lifting$),顾名思义就是翻倍。它能够使线性的处理转化为对数级的处理,大大地优化时间复杂度。
这个方法在很多算法中均有应用,其中最常用的是 $\tt RMQ$ 问题和求 $\tt LCA$(最近公共祖先)。
实现:如何编写
基础:基本结构
显而易见,首先是需要预处理,而预处理也十分简单。我们定义数组 $st[N][lg[N]]$ 因为我们是以 $2$ 的幂次分组,所以第二维只需要开 $\log n$ 的大小。首先从低次幂开始,因为递推的需要,从低次幂开始把每一位的值预处理出来以后在继续预处理。
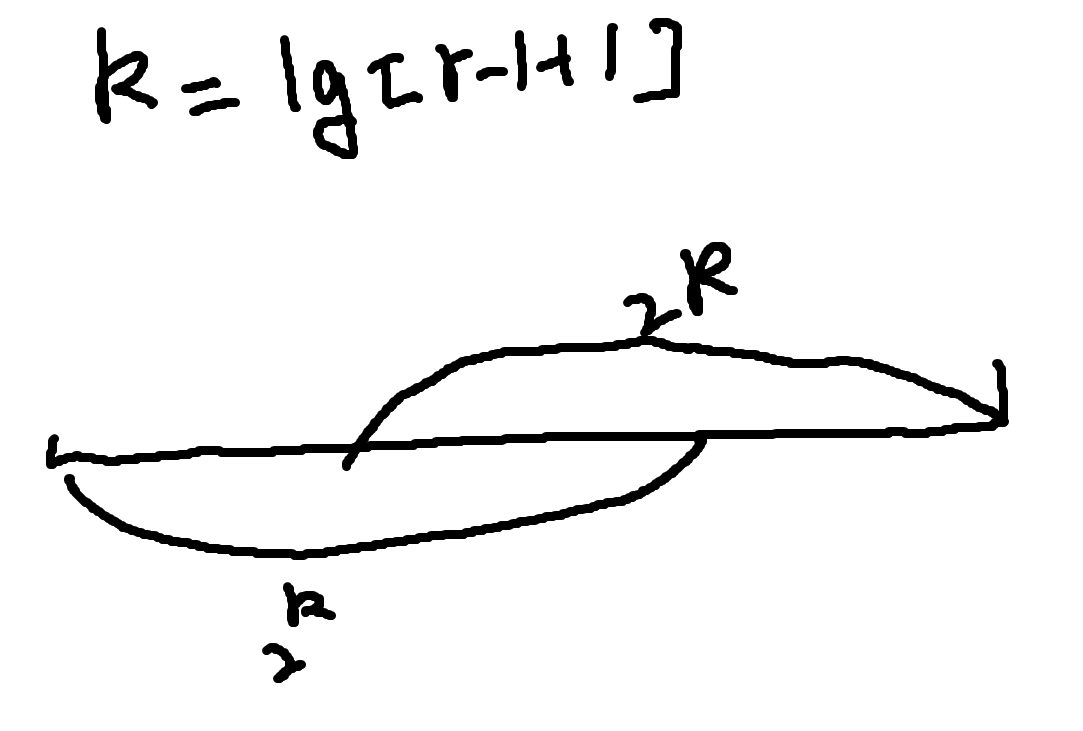
查询的时候我们考虑如何查询,因为我们的目标是 $O(1)$ ,所以肯定不可以从 $1$ 开始 $2$ 次幂跳。由于对于最值操作,重复是没有问题的,所以就不难得出:
1 | min(st[l][lg[r - l + 1]], st[r - (1 << (r - l + 1)) + 1][lg[r - l + 1]]); |
如图:
总结:完整模板
1 | int lg[100010]; |