算法简介：稳固阵线的魄力

实话实说，这个被叫做基环树东西，没有什么强制的算法。本质上来讲，这是一种特殊的图，因为他特殊的性质，存在一种方式去统计和综合上面的信息，所以被单独拿出来讲了。

基环树，这个名字可以仍未是基于环的树，这个思维去解决问题的思路，还有答案的计算已经图的构建，都和环离不开关系，所谓基环基环，就是有环且仅有一个环的树。有时候也被称为章鱼图

算法基础：诱导殉爆的狙击

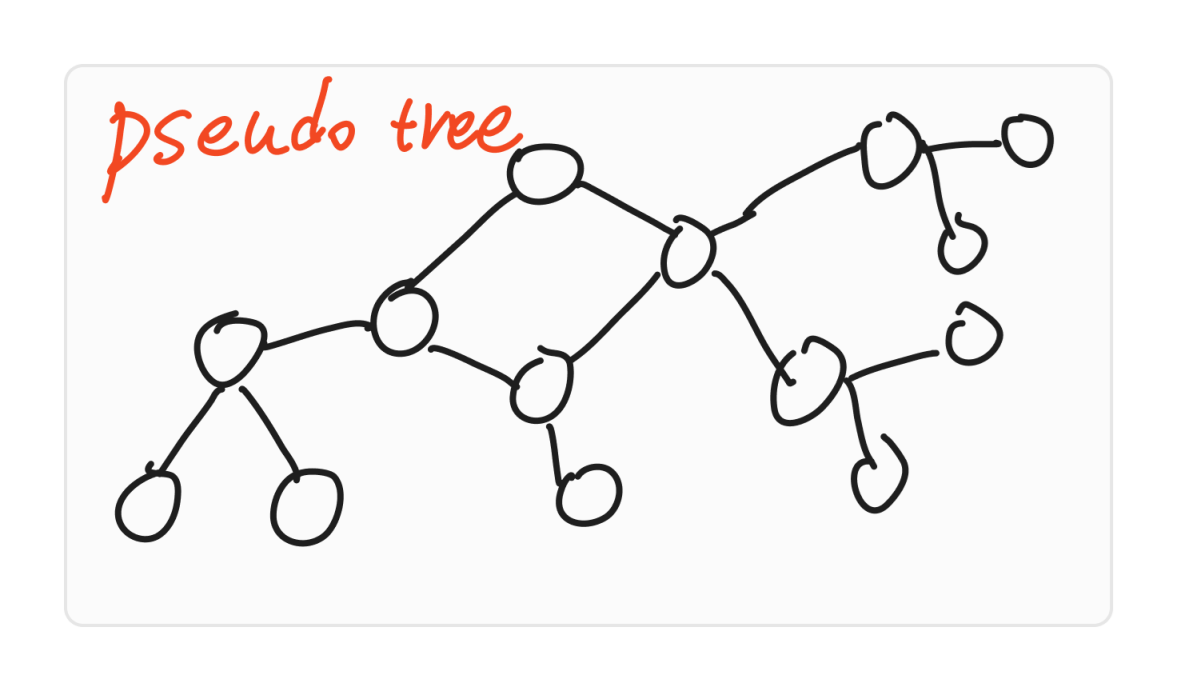
那么首先，我们来介绍基环树的基本相关内容，首先给出一个基环树的图片。

基环树结构

说实话，这张图片可能画的不够明显。我们会发现这个被称为基环树的结构分为两个部分：

  1. 中间的环。树周围的分支，都围绕着中间的那四个环节点连出来。
  2. 周围的支。环的每一个节点，都可以看做一个以当前环节点为根的子树。

这和基环树的定义有关，一棵树增加一条边使得原图存在了一个环，这就是基环树。

而基环树处理问题的思路，就是分别处理每一个子树，然后再通过环统计一些答案。这就是基环树处理问题的基本思想，下面给出一个实例尝试一下。

算法演示：娴熟复装的技巧

那么我们现在就给出演示实例。比如说我们要求基环树的直径，或者说距离最远的两个点对。这里给出一道例题：IOI2008 Island - 洛谷 | 计算机科学教育新生态

模型构建：线列枪刺

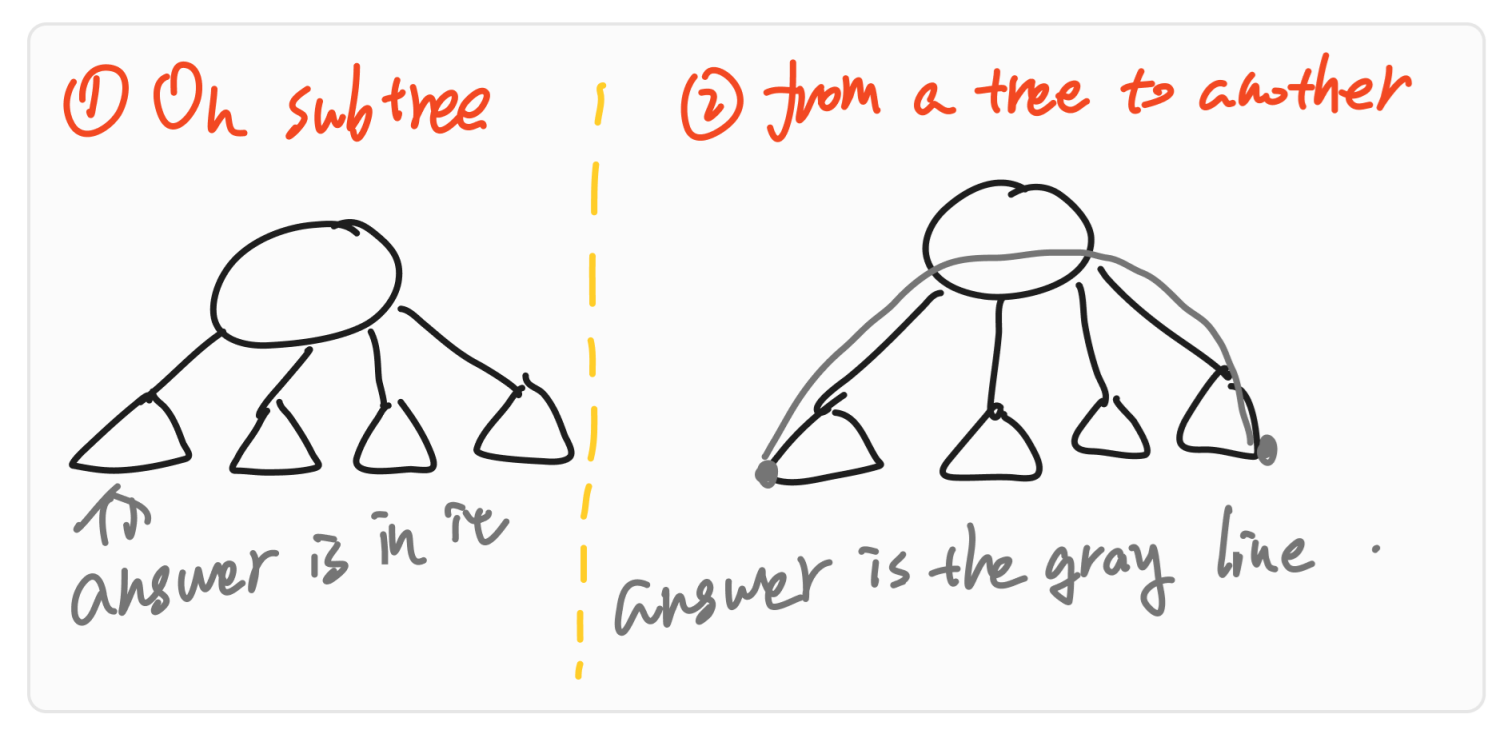
这道题给出的其实也不是基环树，是若干棵基环树，也就是所谓基环森林，但是换汤不换药，我们首先来看看单个的基环树如何解决。首先考虑答案的可能性，大致就是两种。

答案的种类

那么这两种情况中的第一种。其实就是子树的直径罢。这个没话说，但是对于两个子树之间的连接，又要如何考虑呢？由于只存在一个环，而第一种类型和第二种类型我们都是在基于环的基础上搞定的，所以我们优先考虑如何找到一个环。

环与直径：急促拦射

首先，就是找环。这个部分其实卡了我很久，我最初的代码的问题就出现在找环上，之后最后差点 AC 的代码问题也是在找环上，可以说这个找环是罪大恶极、罪孽深重。

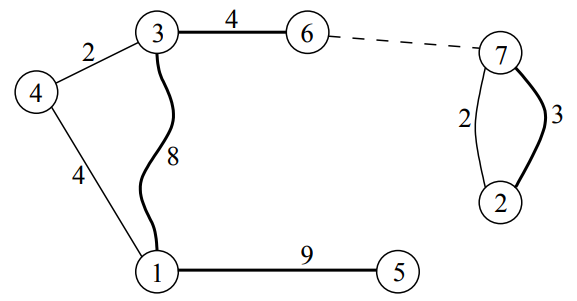
为什么这么说，不就是一个找环吗？有什么难的。但是我们首先观察题目给出的样例：

样例图示

如果，你是和我一样，一开始记录环的时候是不给走父亲，那么你会把环 2 -> 7 -> 2 算成一个链，而不是一个环。那么就需要标记边，而如何标记边？只能用链式前向星了。你若是用 vector 乱搞也不是不行

确保了环不会少算或者漏算，那么如何标记一个环呢？这里给出一个思路，我们可以用一个返回值为 bool 的 DFS 来记录当前这个点是不是在环上的。如果你走到了一个点，他是已经访问过的，说明这里有一个环，那么就可以把他当成环的起点，回溯找到整个环，这时候的返回值都是 true ；但是如果你回溯到了环的起点，那就说明一个环结束了，那么这之后回溯到的内容就不再属于环里面了，返回 flase 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool GetCircle(int u, int la) { // la 是父亲走向自己的那条边的编号
    if(vis[u] == 1) {
        vis[u] = 2; Cir[++tot] = u; vis2[u] = 1;
        // vis 表示这个点访问过没有，第二次访问的点也就是环的起点标记为 2
        // Cir 是存下来的环节点，vis2 记录是不是环节点，这个之后要用到
        return 1;
    }
    vis[u] = 1;
    for(int i = G.head(u); i; i = G.nt(i)) {
        int v = G.to(i);
        if(i != ((la - 1) ^ 1) + 1 && GetCircle(v, i)) {
            if(vis[u] != 2) { // 表示这个点不是环的起点，那就继续
                Cir[++tot] = u; vis2[u] = 1;
                dis[tot] = dis[tot - 1] + G.wt(i);
	            return 1;
            }
            else { // 否则的话，环就已经终结了
                dis[0] = dis[1] - G.wt(i);
                return 0;
            }
        }
    }
    return 0; // 无关节点还是无用的
}

那么基本的环找到了，就得是寻找每个树的内容了，首先，我们处理第一种情况，但在一个子树内的直径，十分好做，就是最基础的树形 DP 求直径。为什么要用树形 DP 求直径而不是 DFS 两次呢？

我们考虑动态规划的做法会是什么样的，我们设 $dp[i]$ 表示以 $i$ 为起点，往深度大的节点可以走的最远距离。那么动态规划的方程显而易见是非常简单的：

1
dp[u] = max(dp[u], dp[v] + G.wt(i));

那其实答案也就好说了，由于直径是不可以有重复边的，所以说呢，我们肯定是找到一条最大值和一条次大值，而最大值一定是在 DP 不断地递推过程中找到的，次大值就可以用当前儿子一遍一遍试过来，那么求子树内直径还有动态规划求一个点向外走的最远距离的方式就好搞了。

1
2
3
4
5
6
7
8
9
10
11
void GetDiameter(int u) {
    vis2[u] = 1;
    for(int i = G.head(u); i; i = G.nt(i)) {
        int v = G.to(i);
        if(vis2[v]) continue;
        GetDiameter(v);
        // ans 就是这个基环树的答案，由于单个直径也算在答案情况之中，所以直接就标记了
        ans = max(ans, dp[u] + dp[v] + G.wt(i));
        dp[u] = max(dp[u], dp[v] + G.wt(i));
    }
}

环上统计：掷弹爆轰

那么我们现在就成功处理完了每一个点向外走走出的最远距离，接下来就是统计两个子树之间的答案了。我们要统计两个子树之间的答案，可以写出下面的等式来表示答案的形式：

这里的 $dp[u]$ 就是上文中搞定的一个点向外走的最远距离。$\operatorname{dis}(u,v)$ 表示环上两点的最大距离，因为环上有两条路径嘛，但是我们要求最长链，所以说肯定是取最长路径。

上面在处理环的的时候，会注意到有一个 dis 数组，这个就是我们处理的环上距离的前缀和，他表示从环上第一个点到当前点的距离。那么我们就可以把刚刚的答案改成前缀和的形式：

当然这样的式子是有缺陷的，不过先不要经，我们把 “ 同类项 ” 合并一下，就会变成下面的二式。联系到环的最大长度就是 $n-1$ 并且曾经我们学过的破环为链的技巧，单调队列就已经呼之欲出。

1
2
3
4
5
6
7
8
9
10
11
12
13
inline void CalcCircle() {
    for(int i = 1; i <= tot; i++) {
        a[i + tot] = a[i] = dp[Cir[i]];
        dis[i + tot] = dis[i + tot - 1] + dis[i] - dis[i - 1];
    }
    deque<int> q;
    for(int i = 1; i <= 2 * tot; i++) {
        while(q.size() && q.front() <= i - tot) q.pop_front();
        if(q.size()) ans = max(ans, a[i] + a[q.front()] + dis[i] - dis[q.front()]);
        while(q.size() && a[q.back()] - dis[q.back()] <= a[i] - dis[i]) q.pop_back();
        q.push_back(i);
    }
}

那么最后答案就是这样了，这个只是求得了一个基环树。但是原图是一个基环森林，肯定不止一棵基环树，所以说最终的答案就是所有基环树的总和加起来，这样就正式做完了这道题。下面附上一个卡掉我的样例：

1
2
3
4
5
4
2 10
3 1
2 1
2 10

最终代码：协同战法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

template<int N, int M>
class Graph {
    private :
        struct Edge {
            int to, nt, wt;
            Edge() {}
            Edge(int to, int nt, int wt) : to(to), nt(nt), wt(wt) {}
        }e[M];
        int hd[N], cnte;
    public :
        inline void clear() { memset(hd, 0, sizeof(hd)), cnte = 0; }
        inline void AddEdge(int u, int v, int w = 0) {
            e[++cnte] = Edge(v, hd[u], w);
            hd[u] = cnte;
        }
        inline int head(int u) { return hd[u]; }
        inline int nt(int u) { return e[u].nt; }
        inline int to(int u) { return e[u].to; }
        inline int wt(int u) { return e[u].wt; }
};

const int MaxV = 1e6 + 10;
const int MaxE = 2e6 + 10;

int n;
Graph< MaxV, MaxE >G;

inline void Input() {
    read(n);
    int v, w;
    for(int i = 1; i <= n; i++) {
        read(v, w);
        G.AddEdge(i, v, w);
        G.AddEdge(v, i, w);
    }
}

int vis[MaxV], vis2[MaxV];
int Cir[MaxV], tot;
ll dis[MaxV << 1];

bool GetCircle(int u, int la) {
    // cout << u << ' ' << "\n";
    if(vis[u] == 1) {
        vis[u] = 2; Cir[++tot] = u; vis2[u] = 1;
        return 1;
    }
    vis[u] = 1;
    for(int i = G.head(u); i; i = G.nt(i)) {
        int v = G.to(i);
        if(i != ((la - 1) ^ 1) + 1 && GetCircle(v, i)) {
            if(vis[u] != 2) {
                Cir[++tot] = u; vis2[u] = 1;
                dis[tot] = dis[tot - 1] + G.wt(i);
            }
            else {
                dis[0] = dis[1] - G.wt(i);
                return 0;
            }
            return 1;
        }
    }
    return 0;
}

ll res, ans;

ll dp[MaxV];

void GetDiameter(int u) {
    vis2[u] = 1;
    for(int i = G.head(u); i; i = G.nt(i)) {
        int v = G.to(i);
        if(vis2[v]) continue;
        GetDiameter(v);
        ans = max(ans, dp[u] + dp[v] + G.wt(i));
        dp[u] = max(dp[u], dp[v] + G.wt(i));
    }
}

ll a[MaxV << 1];

inline void CalcCircle() {
    for(int i = 1; i <= tot; i++) {
        a[i + tot] = a[i] = dp[Cir[i]];
        dis[i + tot] = dis[i + tot - 1] + dis[i] - dis[i - 1];
    }
    deque<int> q;
    for(int i = 1; i <= 2 * tot; i++) {
        while(q.size() && q.front() <= i - tot) q.pop_front();
        if(q.size()) ans = max(ans, a[i] + a[q.front()] + dis[i] - dis[q.front()]);
        while(q.size() && a[q.back()] - dis[q.back()] <= a[i] - dis[i]) q.pop_back();
        q.push_back(i);
    }
}

inline void Work() {
    for(int i = 1; i <= n; i++) {
        if(vis2[i]) continue;
        ans = tot = 0;
        GetCircle(i, 0);
        for(int j = 1; j <= tot; j++) {
            GetDiameter(Cir[j]);
            // cout << Cir[j] << ' ';
        }
        // cout << endl;
        CalcCircle();
        res += ans;
    }
    printf("%lld\n", res);
}

int main() {
    int T = 1;
    while(T--) {
        Input();
        Work();
    }
    return 0;
}

算法细节：多重速射的秘诀

Q：如何判断一个题目是基环树？
A：一般来讲都会有明显的说明类似于 “每个连通块有且只有一个环” 或者更加通用的 “ n 个点 n 条边 ”。

Q：基环树的常用手段？
A：多，多去了。常见的是刚刚的例题给环上节点赋权，然后进行操作；还有的是删除环上一条边，然后操作。

Q：基环树常用数据结构？
A：这还真不好说，但是常见的就是线段树、单调队列、动态规划等等

Q：如何做好基环树的题目？
A：根据我们老师的说法（其实在甩锅的qwq），基环树比较考验对于基础知识的掌握，是极其灵活的数据结构，题目只是给我们提供了常用思路而已。

算法实战：增量火力的毁伤

查看相关算法标签喵！

参考资料（以下排名不分先后）：