算法简介：玉颗珊珊月中落

这篇文章是字符串算法的大集合，会提到字符串哈希，字典树，KMP以及AC自动机等常用算法。字符串哈希作为非常常用的基本手段，是读者不得不会的一种算法。KMP 算法可以快速地经行字符串的匹配、比对，以及他和字典树的结合体，AC自动机，都是非常重要的知识点。

算法演示：云台团团降芦菔

字符串哈希：妙受琼阁

那么作为最最基础的，这个字符串哈希应该最先讲。字符串哈希的主要思路，就是把这个字符串看成一个高进制数，从而进行比对的一种哈希算法。

那么说到把字符串转化为高进制数，不难想到位值原理，就是说每一位的值都是不一样的，对于 $B$ 进制数的第 $i$ 位（个位算作第 $0$ 位，十位是第 $1$ 位，以此类推）这一位上的 “ $1$ ” 表示的是 $B^i$ 。

那么常规的，我们考虑到数字上的一些习惯，我们不妨也设这个字符串数字的左边是高位，右边是地位，那么如何去哈希呢？不难想到了其实：

这一个式子中，$hash_i$ 表示前 $i$ 位的哈希结果，$Base$ 表示这个字符串数字是几进制，$Hash(s_i)$ 表示这个字符串第 $i$ 位的哈希值（可以直接用 ASCII ）。

那么哈希自然是要取模的，纠结了那么久，这个 $Base$ 和 $Hash(x)$ 怎么取呢？我个人有几种常用的方法：

  1. $Base = 31$ 这种我通常用来做只有小写（或只有大写）的字符串哈希题目，$MOD = 2^{64}$ 这个的意思是直接自然溢出，给哈希数组开了 $\tt unsigned\ long\ long $ 然后自然溢出，这是一个不错的办法（毕竟有一次单哈希不管取什么常见的模数都挂了，那就只能自然溢出了，，，）
  2. $Base = 131$ 这个我用来做有其他字符的，哈希值直接就是这个字符的 ASCII 编号，很方便。

前缀字典树：正思无邪

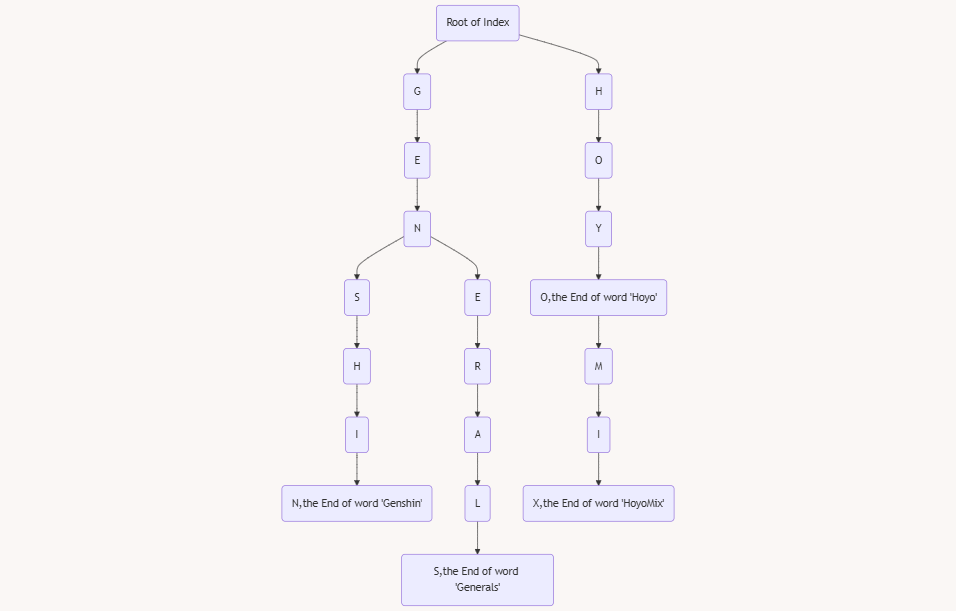
字典树，又称前缀树，英文名称 $\tt Tire$ 树。顾名思义，就是像字典一样的树。我们思考一下字典的索引结构，他一定是如下图所示：

而这张图也能充分的表现出字典树的结构

  1. 每一个点表示一个字母，从根到该节点的路径可以凑成一个单词。每一个单词的末尾会打上一个结束标记
  2. 单词是可以重叠的，这样子才能节省空间

但是我们会发现，字典树的空间，很玄学！只要题目数据给的够玄学，你就不知道你的空间怎么开。这怎么办？有一种很玄学的写法：指针。这里就直接给出模板了，拿走不谢。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
struct Node {
    Node* ch[30];
    bool mark;
    Node() {
        memset(ch, NULL, sizeof(ch));
        mark = false;
    }
};
class Tire {
private :
    Node* root;
public :
    Tire() { root = new Node(); }
    inline Node* rt() { return root; }
    inline void insert(string s) {
        Node* p = root;
        for(char c : s) {
            if(p->ch[c - 'a'] == NULL) {
                p->ch[c - 'a'] = new Node();
            }
            p = p->ch[c - 'a'];
        }
        p->mark = true;
    }
    inline bool find(string s) {
        Node* p = root;
        for(char c : s) {
            if(p->ch[c - 'a'] == NULL) {
                return false;
            }
            p = p->ch[c - 'a'];
        }
        return p->mark;
    }
};

ＫＭＰ算法：爰爰可亲

KMP 算法，全称 $\tt Knuth–Morris–Pratt $ 算法，KMP取的是这三个人名的开头。KMP是一种通过减少错误匹配次数，从而优化复杂度的算法。

既然要知道KMP算法的好处，那么首先得知道没有优化的暴力是怎么样的。我们设主串 S = generalsgenshin ，模式串 t = genshin ，那么匹配会是这样的：

g e n e r a l s g e n s h i n
g e n s h i n

我们匹配到模式串的 ‘s’ 的时候，就发现匹配不上了，那么接着一长串 ‘enerals’ 都是第一个字母就和匹配串不一样，然后匹配到 genshin，才匹配结束。

这样的算法复杂度，显而易见是 $O(n^2)$ 的，非常的不优秀。所以这时候KMP算法就出来了。他的优化之处就在于：节省掉了无用的匹配 ‘enerals’ 的过程，直接匹配 genshin 。

那么它是如何实现这样的功能的呢？

我们发现，当一个东西匹配失败的时候，其实没有必要全退了，我们可以从最后一个匹配的开始，继续往后，而这里就需要用到一个数组 $next$ ，他的作用在于告诉我接下来跳到哪里。她表示的是前缀的真前后缀（不等于原串的前缀或后缀）最长的一样的部分。

那么我就举个例子来看看。用字符串 yaoyao

  1. 前缀 y ，没有不等于原串 y 的前缀或后缀，0
  2. 前缀 ya ，没有相同的真前后缀，0
  3. 前缀 yao ，同样没有，0
  4. 前缀 yaoy ，这里有了相同的真前缀 y ，长度是 1 。
  5. 前缀 yaoya ，这里是相同真前缀 ya ，长度为 2 。
  6. 前缀 yaoyao ，相同真前缀 yao ，长度为 3 。

模拟了一遍，应该就都知道意思了罢？

那么有了这个 $next$ 数组，我们就可以是是按照刚刚的意思做一做KMP了。给出主串 yayyaoyao ，模式串 yaoyao ，试着匹配一下：

  1. 首先处理出 $next$ 数组，以及处理过了，过程在上面自己看。
y a o y a o
0 0 0 1 2 3
  1. 然后就可以开始匹配了：
y a y y a o y a o
y a
模式串第二个匹配不上了，
查询 next[1] 是 0		 o y a o
y
模式串第一个就匹配不上，
直接跳下一个		 a o y a o
y a
又匹配不上了，
next[1] = 0		 o y a o
y a o y a o
终于匹配上了

那么这里的代码也就很好写了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void get_Next(string s, int next[])	{	//这个函数对字符串s进行预处理得到next数组
    int j = 0;
    next[0] = 0;	//初始化
    for(int i = 1; i < s.size(); i++) {	//i指针指向的是后缀末尾，j指针指向的是前缀末尾
        while(j > 0 && s[i] != s[j]) j = next[j-1]; //前后缀不相同，去找j前一位的最长相等前后缀
        if(s[i] == s[j]) j++;    //前后缀相同，j指针后移
        next[i] = j;    //更新next数组
    }
}
int strSTR(string s, string t) {//这个函数是从s中找到t，如果存在返回t出现的位置，如果不存在返回-1
    if(t.size()==0)	return 0;
    get_Next(t, next);
    int j = 0;
    for(int i = 0; i < s.size(); i++) {
        while(j > 0 && s[i] != t[j]) j = next[j - 1];	
        if(s[i] == t[j]) j++;
        if(j == t.size()) return i - t.size() + 1;
    }
    return -1;
}

ＡＣ自动机：恻隐本义

那么首先大家一直说AC自动机是 Tire + KMP 这不是没有道理的，AC自动机沿用了 Tire 树的结构，使用了类 KMP 的思想，所以大家才这么表述。AC自动机是一种多模式串匹配的算法，意思就是说对于一个目标串可以一下子匹配好多串。其实的话，他的实现方式比较特殊，有点类似于，建立模式串的 Tire 树，用目标串在 Tire 树上匹配。

那么就来，我们的目标串和模式串如下：

1
2
3
4
5
6
7
S : yaoyaoingenshinismadebymihoyo
T :
ini
yao
mihoyo
yo
made

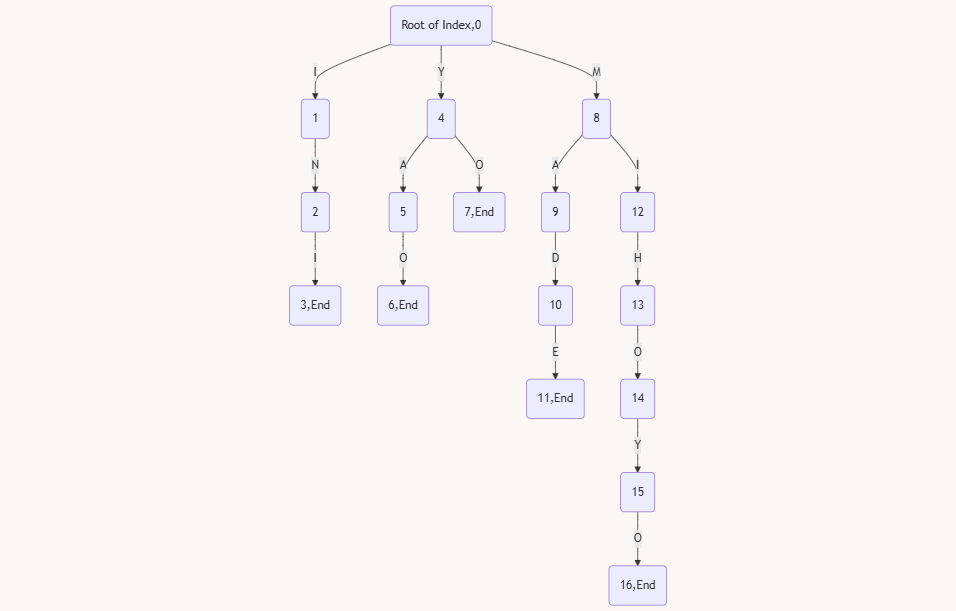
那么就开始构建 Tire 树：

这样就是一个 Tire 树的结构了，那么想要在上面利用 KMP 的思想，我们的 next 数组就要进化成 fail 失配数组了。fail 数组的含义就是当我们匹配不上的时候要跳转到的位置。这里就利用了 KMP 失配跳转的思想，得以减小复杂度。

介于AC自动机的 Tire 结构，如果我们在这颗 Tire 树上匹配目标串的时候，同一个节点可能会匹配很多个模式串。也就是说，我们的 fail 指针是让这个目标串在 Tire 树上来回穿梭。所以我们 fail 数组只需要相同的后缀就可以了。

我们定义 fail 数组是能在 Tire 树上面找到的，最长的，当前字符串（root 到当前点的路径）的后缀，那么我们就来找找这个 Tire 树的 fail 数组。

fail 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
节点 0 0 1 0 0 0 0 0 0 0 0 1 0 0 4 7

意思也很明显了：

  1. 一号点 i 是三号点 ini 的最长的后缀（能找到的
  2. 一号点 i 也是十二号点 mi 的能找到的最长后缀
  3. 四号点 y 是十五号点 mihoy 的最长后缀
  4. 七号点 yo 就是 mihoyo 十六号点的最长后缀了。

其他的找不到的，都是指向根。那么这样一个过程在怎么去求呢？我们肯定首先考虑能不能从已知的推过来。

我们假设存在一条边 $c$ 把 $u$ 和 $v$ 连接起来，其中 $u$ 是父亲。那么有几种可能：

  1. 如果 $fail[u]$ 有一个符合条件的儿子，那么肯定可以接上，这样的就让 $fail[v]$ 直接指向 $fail[u]$ 的那个符合条件的节点。
  2. 如果 $fail[u]$ 没有的话，我们就一直找，$fail[u]$ 不行找 $fail[fail[u]]$ 再不行再找，一直跳到根节点。

那么这样的一个过程，不难想到用广搜实现（似乎深搜也不是不行）但是这样一直跳 $fail$ 就很不方便，搞不好复杂度退化到 $O(n^2)$ 怎么办。这时候我们就想到一个类似的算法，并查集。并查集也是要一路找到最祖先的最先，为了防止这个怎么办，路径压缩。这样就很完美的解决了问题，直接上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Build() {
	queue<int>q;
	memset(fail, NULL, sizeof(fail));
	for(int i = 0; i < 26; i++) {
        if(tr[0][i]) q.push(tr[0][i]);
    }
	while(!q.empty()) {
		int k = q.front(); q.pop();
		for(int i = 0; i < 26; i++) {
			if(tr[k][i]) {
				fail[tr[k][i]] = tr[fail[k]][i];
				q.push(tr[k][i]);
			}
			else tr[k][i] = tr[fail[k]][i];
		}
	}
}

我们这个路径压缩的过程，就是一个把字典树改造成字典图的过程，字面意思，这个概念了解就好。

求出了 $fail$ 指针，查询就变得十分简单了。

为了避免重复计算，我们每经过一个点就打个标记为 $−1$ ，下一次经过就不重复计算了。

同时，如果一个字符串匹配成功，那么他的 $fail$ 也肯定可以匹配成功（后缀嘛），于是我们就把 $fail$ 再统计答案，同样， $fail$ 的 $fail$ 也可以匹配成功，以此类推……经过的点累加 $flag$ ，标记为−1−1。

最后主要还是和 Tire 的查询是一样的。

1
2
3
4
5
6
7
8
9
10
int query(char *t) {
	int p = 0, res = 0;
	for(int i = 0; t[i]; i++) {
		p = tr[p][t[i] - 'a'];
		for(int j = p; j && ~e[j]; j = fail[j]) {
            res += e[j], e[j] = -1;
        }
	}
	return res;
}

那么总体的代码也就出来了。这里也给出模板，拿走不谢（模板来自洛谷日报）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const int N=1000;
struct AC_automaton{
	int tr[N][26],cnt;//TRIE
	int e[N];//标记字符串结尾
	int fail[N];//fail指针

	void insert(char * s){//插入模式串
		int p=0;
		for(int i=0;s[i];i++){
			int k=s[i]-'a';
			if(!tr[p][k])tr[p][k]=++cnt;
			p=tr[p][k];
		}
		e[p]++;
	}
	void build(){
		queue<int>q;
		memset(fail,0,sizeof(fail));
		for(int i=0;i<26;i++)if(tr[0][i])q.push(tr[0][i]);
			//首字符入队
			//不直接将0入队是为了避免指向自己
		while(!q.empty()){
			int k=q.front();q.pop();//当前结点
			for(int i=0;i<26;i++){
				if(tr[k][i]){
					fail[tr[k][i]]=tr[fail[k]][i];//构建当前的fail指针
					q.push(tr[k][i]);//入队
				}
				else tr[k][i]=tr[fail[k]][i];
					//匹配到空字符，则索引到父节点fail指针对应的字符，以供后续指针的构建
					//类似并差集的路径压缩，把不存在的tr[k][i]全部指向tr[fail[k]][i]
					//这句话在后面匹配主串的时候也能帮助跳转
			}
		}
	}
	int query(char *t){
		int p=0,res=0;
		for(int i=0;t[i];i++){
			p=tr[p][t[i]-'a'];
			for(int j=p;j&&~e[j];j=fail[j])res+=e[j],e[j]=-1;
		}
		return res;
	}
};
AC_automation ac;

算法实战：踮脚蹑蹑影轻踪

查看相关标签喵！