算法简介：水中幻愿

这是一篇关于二分图的全面讲解，里面会从二分图的基本介绍开始，到匈牙利算法的几个运用。二分图的大多数题目就是这些了。接下来我们就开始最最基础的讲解。

算法介绍：星命定轨

二分图检验：灭绝的预言

所谓二分图，主打一个二分。指的是如果一个图的点可以分为两个不重合的点集 $U,V$ ，且只有 $U,V$ 两个点集间有点连通，同一个点集内没有边连通的图。

那么首先，对于一张图，如果他没有环，他一定是二分图。毕竟如果没有环，我只需要奇偶奇偶的分开就可以，都不需要担心会有环边在一个点集内。但是如果有环就不一样了，我们来看下面的两个图，分别代表的是奇环和偶环。

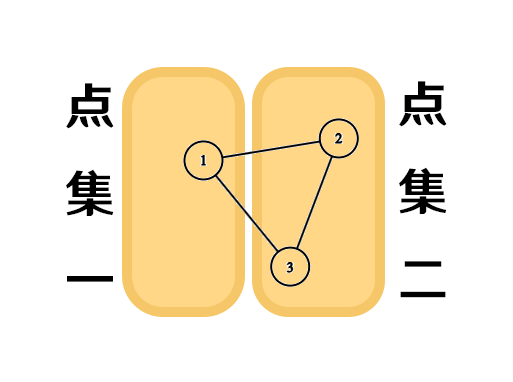
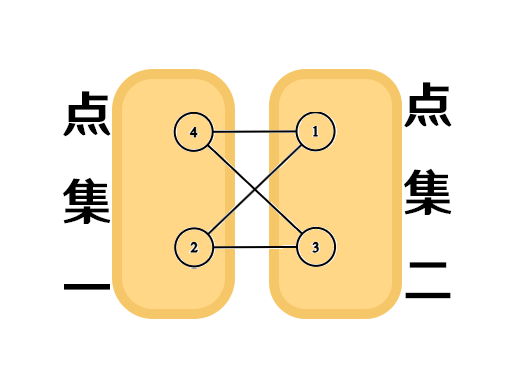
我们发现，对于偶环还是奇偶分点集没有问题。但是对于奇环，就不一样了，因为容斥原理，最后一定会多一个，而这个多出的一个，就会导致他会比偶环在某一个点集里有一条边相连，这样是不符合二分图条件的。所以说，验证二分图的本质其实就是判断奇环，奇偶染色。

int flag[N]; // 0 未走过 1 奇 2 偶
Graph G;
void Dfs(int u, int fa) {
    flag[u] = 3 - flag[fa]; 
    for(int i = G.head(u); i ; i = G.nt(i)) {
        int v = G.to(i);
        if(v == fa) continue;
        if(!flag[v]) {
            Dfs(v, u);
        }
        else if(flag[v] == flag[u]) {
            return false;
        }
    }
    return true;
}

匈牙利算法：命运的嘲弄

那么接下来就是二分图最最常用的算法，匈牙利算法了，匈牙利算法主要有 3 个应用，最大匹配，最小点覆盖，最大独立集。那么我们首先来讲最简单的最大匹配算法。

我们给出一张例图以及如下定义：

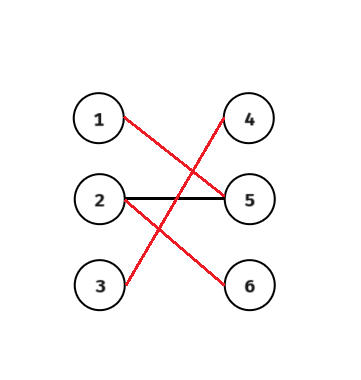
已盖点：已经被匹配的点，例图中所有点点都是已盖点
未盖点：未被覆盖的点，例图中没有这种点。
匹配边：在这个匹配中增加这一条边前，两个点都是未盖点，连接后两个点都是已盖点，例图中红色的边都是匹配边。
最大匹配：这张二分图中最多的匹配数量。例图中的最大匹配是 3 。
完全匹配：有至少一个点集的店被匹配完了。例图就是一个完全匹配。
完美匹配：所有点都匹配了。例图也是一个完美匹配。

那么我们在这里先大概将一个匈牙利算法求最大匹配的流程：首先，我们找到一个点，然后随便找一条边，接着考虑，如果我们能找到一个路径，起点是未盖点，终点也是未盖点，中间经过的是已盖点。拿例图举个例子，如果我们一开始随便选了黑色的边，然后就可以找到 $1\rightarrow5\rightarrow2\rightarrow6$ 这样的路径，用 $1\rightarrow 5$ 和 $2\rightarrow6$ 替换 $5\rightarrow 6$ ，造成了 1 的价值。这样的路径被称为增广路。那么接下来就直接上代码。

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i) {
    for (int j = 1; j <= N; j++) {
        if (Map[i][j] && !vis[j]) { //有边且未访问
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) { //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int MxCheck() {
    int cnt = 0;
    for (int i = 1; i <= M; i++) {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}

最小点覆盖：星月的连珠

匈牙利算法的第二个应用就是最小点覆盖了，我们定义覆盖：当选中一个点时，会覆盖与他直接相连的所有边。最小点覆盖就是：选择最少的点，覆盖这张图所有的边。

我们也是直接再拿出一张图：

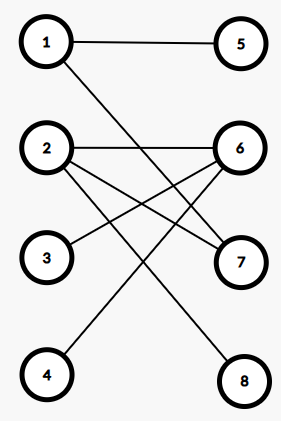
那么这里引入一个定理：Konig 定理，讲的就是最小点覆盖 = 最大匹配。
对应的计算最小点覆盖的算法是：第一步先做最大匹配，之后我们每次从左边不在匹配边中的一个点开始去按照：未匹配边 -> 匹配边 -> 未匹配边 -> 匹配边 …… 匹配边与未匹配边交替选择的顺序，标记途中经过的顶点，则最后一条经过的边必定为匹配边。这里我开了两个数组 vx 和 vy 分别记录每个左侧点是否被标记和每个右侧点是否被标记，上面的例子中3、4、6被标记，但务必牢记最后最小点覆盖的点集并不是这些点组成的集合，而是左侧未被标记的点和右侧被标记的点组成的集合S才是最终答案。

那么为什么呢，看如下证明：

我们设选出的点集为 $P$ ，最大匹配的边集是 $E$，那么首先要证明的是数据没问题，也就是说我们的 $P$ 是否覆盖了所有边。

证明：我们假设有一条边左右两端点均不在 $P$ 集合中，则左端点被标记，右端点未被标记。分类讨论，如果说当前边不在边集 $E$ 中，则左端点为未被匹配点，又因为当前边不是匹配边，所以必然会从左端点沿当前边开始标记，那么右端点必然被标记，矛盾。如果说当前边在边集 $E$ 中，其左端点被标记，那么必然是通过右端点链接过来的，则右端点被标记，矛盾。综上，我们可以知道点集 $P$ 覆盖了所有边。
那么其次就是证明 Konig 定理的正确性，也就是，$|P| = |E|$ 。

证明：我们知道点集 $P$ 中的左侧点都是匹配点，而右侧点也都为匹配点，又因为一条匹配边上左侧点和右侧点不可能同时在或者不在点集 $P$ 中，那么 $E$ 集合中任意一条边左右两端点中都恰好仅有一个点在点集P中，所以 $|P| = |E|$ 。
再就是保证答案是对的也就是 $P$ 已经是最小的满足条件的点集了。

证明：已知 $|P| =$ 最大匹配数，如果另一个点集的元素个数比 $|P|$ 更小，那么这个点集必然无法包含所有的匹配边，连所有的匹配边都无法全部包含，怎么可能包含所有边呢。所以 $|P|$ 是最小的点覆盖数。

这里要求最小点覆盖，就是直接输出最大匹配数就可以了。

最大独立集：不休的天象

首先介绍这个最大独立集的概念，再这张图中选出一个点集 $U ∈ V$（ $V$ 是图的节点全集）使得这个集合中的点两两之间不连通。

有了概念，我们来想想怎么求最大独立集。

设最大独立集数为 $U$ ，最大匹配数为 $M$ ，$M$ 覆盖的顶点集合为 $P$ 。

首先由于 $M$ 中的两个端点是连接的，所有 $M$ 中必至少有一个点不在 $U$ 集合中，所以 $|M|\le|V|-|U|$

然后我们设一个边 $(x,y) ∈ M$ ，肯定的 $|U|\ge|V|-|P|$ ，如果放入一个 $M$ 集合中的端点，会怎么样呢？如果存在一个 $(a,x),(b,y)$ 且 $a,b$ 不在 $P$ 集合中。如果存在一条边 $(a,b)$ 那么一定存在一个更大的匹配，矛盾；如果不存在 $(a,b)$ 那么一定会存在一个新的增广路 $a\rightarrow x\rightarrow y \rightarrow b$ ，所以说一定会有一个更大的匹配，也矛盾了。所以说，取任意一个 $M$ 的端点肯定不会和 $U$ 中的任意一个点相连，也就是说 $|U|\ge |V|-|P|+|M|=|V|-|M|$ 。

这里就得出了 $|U|\ge |V| - |M|$ 且 $|U|\le |V|-|M|$ 也就是说，$|U|=|V|-|M|$ 。

算法实战：虚实流动

查看相关标签喵！