概念：什么是树状数组？

需求：发现问题、提出问题

在信息学竞赛中，我们经常会遇到求一段区间和的题目。一般来说，我们就只需要使用前缀和数组这是一个预处理时间复杂度 $O(n)$，单次查询 $O(1)$，修改 $O(n)$ 的算法。显而易见，在遇到一些数据范围特别大，修改次数特别多的题目时，就会发生爆炸。而这时我们需要一个可以均衡这个时间复杂度的数据结构。

构造：寻找解决问题的方案

那么如何制造一个这样的数据结构呢？我们可以从数据结构的根本考虑，数据结构是一种可以将时间和空间均衡，使得解决题目的东西。对于前缀和无法完成的题目，就需要更好的数据结构。不可能会有时间短，空间小，功能强大的数据结构，想要让时间变少，就得用空间换，想要让空间少，就得用时间换。我们可以对于基本的数据结构经行比较。

单点修改时间复杂度 区间查询时间复杂度 期望效果
数组 $O(1)$
显而易见的，对于当前的点经行修改便是		 $O(n)$
对于区间 for 一遍求解		 由于想要使前缀和数组的单点修改复杂度降低、
综合数组的区间查询，作为代价，必须要增加这里的时间复杂度
前缀和 $O(n)$
当前缀和中一个点修改时，之后的所有点都要修改		 $O(1)$
$cnt[r] - cnt[l - 1]$		 同样的，这里单点修改过于慢了，所以要减小

同时，对于我们期望数据结构的空间，也需要适量增加。

数据结构的根本差异是分组。我们可以看看不同分组方式对于数据结构的影响：

分组方式
数组 数组是一对一分组，也就是说，一个下标对应一个数据。
前缀和 前缀和是一对多分组，他的分组条件可以从他的递推公式得出

所以，显而易见的，对于 $cnt_i$ 我们对应的是从 $a_1$ 到 $a_i$ 的所有数字的和

导致数组效率低下的原因是分组过多，对于前缀和效率低下的原因是分组重复过多。所以对于我们期望的数据结构的分组也要考虑。

总之，综合上面说的时间空间限制，以及分组方式，我们可以建立起一个基于前缀和的数据结构。

不难想到，由于前缀和重复过多的分组，我们可以发现对于二进制重复量就可以大大减少，而且时间粗劣估计也可以达到 $O(\log n)$ 。
也就是说我们可以根据二进制拆分成不同次幂唯一性进行分组。

总结：树状数组

树状数组或二叉索引树（英语：$\tt Binary\ Indexed\ Tree$），又以其发明者命名为 $\tt Fenwick$ 树。多用于高效计算数列的前缀和， 区间和。它可以以 $𝑂(\log 𝑛)$ 的时间得到任意前缀和，并同时支持在 $𝑂(\log 𝑛)$ 时间内支持动态单点值的修改。空间复杂度 $𝑂(𝑛)$ 。

实现：如何编写树状数组？

梳理：树状数组的核心思想

树状数组的核心思想是根据二进制拆分成不同次幂的唯一性分组得到的数据结构。

那么，我们来看具体树状数组是如何分组的。不难想到，对于区间 $[1, 100]$ 可以有如下两种分组方式：

我们考虑哪一种方式更适合我们的数据结构，我们可以从代码出发，我们发现第一种更有利于代码的编写，所以选第一种。将其抽象为数学形式就是：

设整数 $x$ 的二进制中为 $1$ 的位（ $2^0$ 即第一位我们认为是第 $0$ 位，$a$ 数组从小到大牌序） $a_1 \dots a_n$ ，其表示权值就分别是 $2^{a_1} \dots 2 ^ {a_n}$ 。则分组表示为：

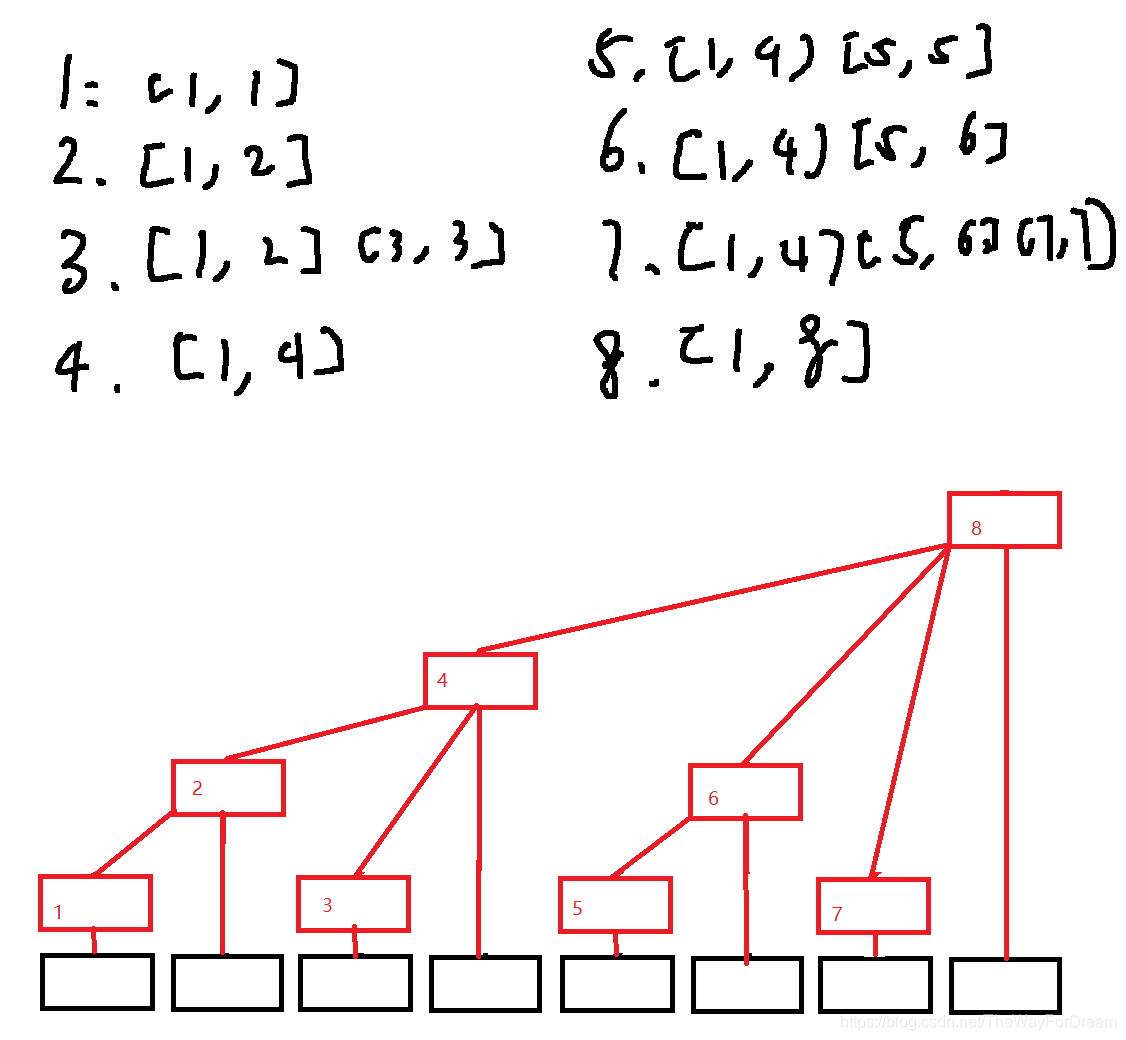
我们设置所谓分组为 $c$ 数组，观察可得如下图（不难发现父子关系是儿子加上他的最低位的 $1$ ）

第一部分： 单点修改

既然树状数组是借助了前缀和思想，那么它建立树状结构的目的就是在 $O(\log n)$ 的复杂度内快速把这一个节点之后的值全都修改了，而前面已经发现父子关系是儿子加上它最低位的 $1$ 。

那么单点修改就可以十分容易的写出来。

1
2
3
4
5
6
7
8
9
10
class BIT {
    private :
    	int c[N];
    	
   		int lowbit(x){ return x & (-x); }
    public :
    	void ModifyPoint(int x, int v) {
            for(int i = x; i <= N; i += lowbit(i)) c[i] += v;
        }
};

第二部分：区间查询

想要求出一段区间的和，根据前缀和可以得知我们可以用 $c[r] - c[l - 1]$ 的方式，那么在树状数组中我们第一步就是要求区间 $[1, x]$ 的和，其实就是数组的 $x$ 前缀和。

代码好写：

1
2
3
4
5
int PreSum(int x) {
    int ans = 0;
    for(int i = x; i >= 1; i -= lowbit(i)) ans += c[i];
    return ans;
}

那么根据前缀和思想，区间查询也好写

1
2
3
int QueryRange(int l, int r) {
    return PreSum(r) - PreSum(l - 1);
}

第三部分：区间修改，单点查询

区间修改是另外一个新的东西，不难想到差分，所以，我们需要树状数组加和减分别表示一个区间的头和尾，利用差分的方式求解。

1
2
3
4
5
ModifyPoint(l, v)
ModifyPoint(r + 1， -v);

//QueryPoint
PreSum(x);

第四部分：区间修改，区间查询

这种就是最难的了，需要重新想。

我们需要考虑如何建模表示 $tree$ 数组。

首先，设更新操作为：在 $[l,r]$ 上增加 $x$ 。我们考虑如何建模维护新的区间前缀和 $c^′[i]$ 。

下面分情况讨论：

  1. $i<l$

这种情况下，不需要任何处理， $c^′[i]=c[i]$

  1. $l<=i<=r$

这种情况下，$c^′[i]=c[i]+(i−l+1)⋅x$

  1. $i>r$

这种情况下，$c^′[i]=c[i]+(r−l+1)⋅x$

因此如下图所示，我们可以设两个树状数组（ $\tt BIT$ ），那么 $c^′[i]=sum(bit_1,i)+sum(bit_2,i)⋅i$ ，对于区间修改等价于：

  • 在 $bit_1$ 的 $l$ 位置加上 $−x(l−1)$ ，在 $bit1$ 的 $r$ 位置加上 $r\ \dot{}\ x$。
  • 在 $bit_2$ 的 $l$ 位置加上 $x$ 的 $r$ 位置加上 $−x$ 。

实践：如何使用树状数组？

例题推荐：

  • HDU1166：敌兵布阵
  • HDU1556：涂气球
  • nyoj233：Sort it
  • POJ2985 The kth Largest Group