前置知识：矩阵快速幂

例一：斐波那契前缀和

直接求斐波那契的例子已经在上面的文章中讲过了。这里直接开始讲斐波那契的前 n 项和怎么算。

求斐波那契的前 $n$ 项和对于 $m$ 取模的结果。

首先，不难给出递推式：

$\begin{cases} f_1 = 1\\ f_2 = 2\\ f_i = f_{i - 1} + f_{i - 2} \quad (i\ge 3)\\ s_1 = 1\\ s_i = s_{i-1} + f_i\qquad (i\ge 2) \end{cases}$

这个是最最基础的递推式子，我们不难想到之前说的列方程法。我们就可以写出下面的方程组。

$\begin{cases} f_{i+1} &= &0\times f_i + 1\times f_{i+1} + 0\times s_i \\ f_{i+2} &= &1\times f_i + 1\times f_{i + 1} + 0\times s_i \\ s_{i+1} &= &0\times f_i + 1\times f_{i + 1} + 1\times s_i \end{cases}$

由于要保证矩阵的特性，所以每一个方程的对应每一项的未知数都得设置成一样的，如果没有这一项，说明系数等于 0 。然后可以写出如下的矩阵乘法：

$\left[\begin{matrix} \ 0&1&0\ \\ \ 1&1&0\ \\ \ 0&1&1 \end{matrix}\right] \times \left[\begin{matrix} \ f_i\ \\ \ f_{i+1}\ \\ \ s_i \end{matrix}\right] = \left[\begin{matrix} \ f_{i + 1}\ \\ \ f_{i+2}\ \\ \ s_{i + 1} \end{matrix}\right]$

可以递推，那么这就是最终的矩阵，显而易见的答案就是 $s_n$ ，最后别忘了取模。

这里附上代码：

inline void Work() {
    Matrix ans(3, 3), now(3, 1);
    ans.mat[0][0] = 0, ans.mat[0][1] = 1, ans.mat[0][2] = 0;
    ans.mat[1][0] = 1, ans.mat[1][1] = 1, ans.mat[1][2] = 0;
    ans.mat[2][0] = 0, ans.mat[2][1] = 1, ans.mat[2][2] = 1;
    now.mat[0][0] = 1, now.mat[1][0] = 1, now.mat[2][0] = 1;
    // cout << ans.power(n - 1) << endl;
    printf("%d\n", (ans.power(n - 1) * now).mat[2][0]);
}

矩阵类在文章开头的链接里自取

例二：佳佳的斐波那契

佳佳定义 $T(n) = (F_1 + 2F_2 + 3F_3 + \dots+nF_n)\mod m$ ，其中 $F_i$ 表示第 $i$ 个斐波那契数。

显而易见的，我们这里还要更加逆天，要求的是一个从来没见过的东西，于是，我们搬出一个古话：

形数结合百般好，隔离分家万事休。—— 华罗庚

我们可以现尝试把这个 T 数列的计算方式画一画，看看有什么特殊的地方。下面三幅图，从左往右依次为：前缀和中的统计，前缀和的前缀和中的统计， T(n) 的统计。

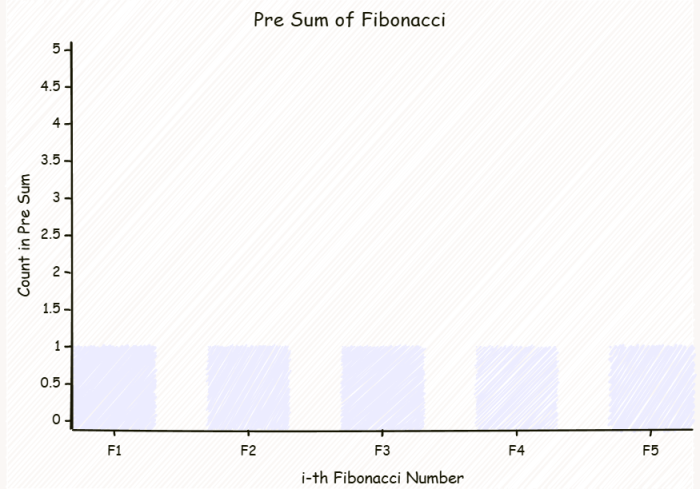
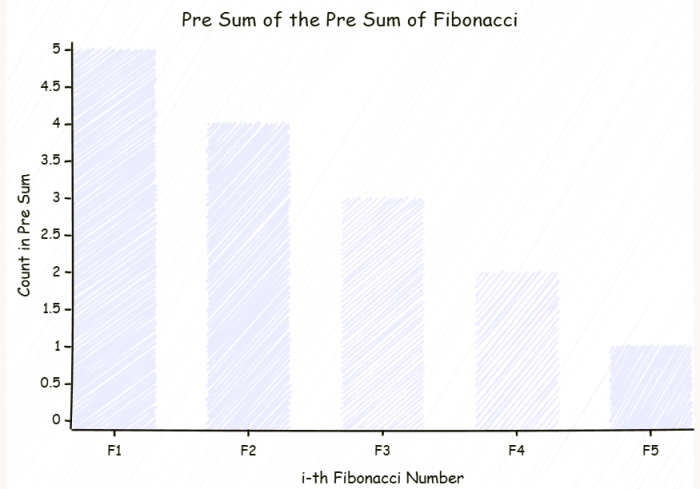
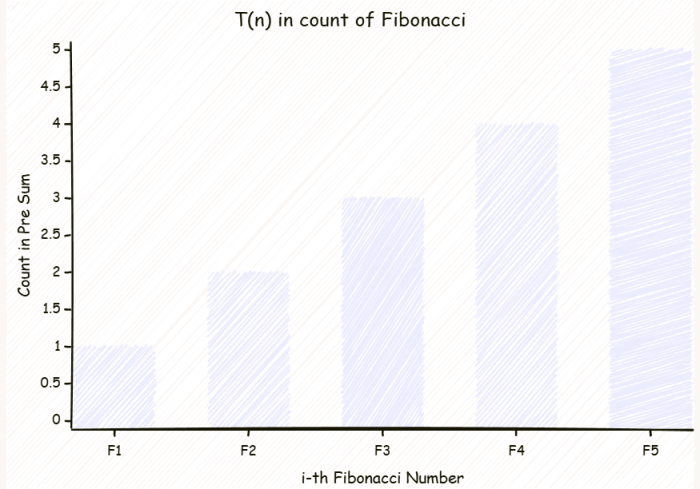
我们不难发现，前缀和的前缀和中每一个斐波那契数的出现次数和题目要求的 T(n) 中每一个斐波那契数的出现次数相当相似。而前缀和是我们能求的，前缀和的前缀和也使我们能求的。那其实就相当于在一个大方块里面，挖掉一角。而这个大方块的计算方式就是：

$S(n)=\sum\limits_{i=1}^n S_i\qquad T(n) = n\times S_n - S(n-1)\quad or\quad T(n) = (n + 1)\times S_n - S(n)$

那么如何去推这样的矩阵呢？显而易见我们比原来的矩阵多了一个需要求的前缀和，但是肯定也难不倒大家，我的代码用的是第一种，多出来的一维矩阵表示的是 $S(n)$ 表示前 $n-1$ 个前缀和的前缀和。

inline void Work() {
    Matrix ans(4, 4), now(4, 1);
    ans.mat[0][0] = 0, ans.mat[0][1] = 1, ans.mat[0][2] = 0, ans.mat[0][3] = 0;
    ans.mat[1][0] = 1, ans.mat[1][1] = 1, ans.mat[1][2] = 0, ans.mat[1][3] = 0;
    ans.mat[2][0] = 0, ans.mat[2][1] = 1, ans.mat[2][2] = 1, ans.mat[2][3] = 0;
    ans.mat[3][0] = 0, ans.mat[3][1] = 0, ans.mat[3][2] = 1, ans.mat[3][3] = 1;
    now.mat[0][0] = 1, now.mat[1][0] = 1, now.mat[2][0] = 1, now.mat[3][0] = 0;
    // cout << ans.power(n - 1) << endl;
    ans = (ans.power(n - 1) * now);
    printf("%d\n", (ans.mat[2][0] * n % P - ans.mat[3][0] + P) % P);
}

至此就是所有的基础斐波那契的矩阵快速幂的题目，比较有意思，也给我们提供了数形结合的新思路。