算法简介：割舍怜悯之心

最小生成树，就是一张图一直删边，直到删成一颗树为止，这叫做生成树，如果这个生成树的边权之和是所有生成树中最小的，那么他被称为最小生成树，前面我们讲过了一个叫做 Boruvka 的算法，虽然他确实是求最小生成树的方法之一，但是他过于远古，不太常用，代码也不如 Kruscal 简单，所以说，我们这里将介绍两种新的最小生成树算法，请看副标题 —— Prim & Kruscal 。

算法演示：割舍侥幸之心

那么最小生成树，生成树生成树，总归就是树，有两种组成部分，一是点，二是边，而 Prim 和 Kruscal 算法分别就是代表了基于点的贪心和基于边的贪心，我们来一个逐个击破。

点贪心：割舍痛苦之心

首先就是 Prim 算法，他之所以被称为点贪心，是因为这样一个思路：

生成树，必须要把一个图的所有点连起来，变成一个树，也就是说，所有点，我们都将出现在最终的点集合里。所以，我们一开始随便选择一个点，加入最小生成树点集合，然后每次去寻找和我们最小生成树点集合最近的一个点，这样就可以保证每次选出来的边是最短的，然后就一直循环往复，直到所有点都选完。

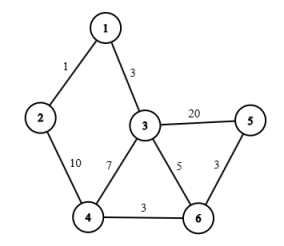
然后，我们就发现，这样的一个过程，和一个最短路算法极其神似，对，就是 $Dijstra$ 算法。$Dijstra$ 算法的原理，就是每次从图里面拿出来一个最近的点去不断更新最短路。而 Prim 算法也是如此。我们可以看个图示：

那么首先根据第一个规则，我们随便选择一个点，比如 $1$ ，那么接下来挑选一个最近的点，显而易见是 $2$ 边权只有 $1$ ，那么现在我们的集合里面有 $1,2$ 然后最小生成树的大小是 $1$ 。

接下来，我们扩张，发现从二出去的唯一一条边 $10$ 太长了，不如从 $1$ 到 $3$ 的那条边，所以说我们扩张到 $3$ 。现在点集里面有 $1,2,3$ 然后最小生成树的大小是 $4$ 。

以此类推，我们会接着扩张到 $6$ ，然后扩张到 $4$ 然后扩张到 $5$ 。然后最小生成树就建完了，总大小应该是 $15$ 。

这样的话，我们就可以写出一个朴素版本的 Prim 代码。

int dis[N], vis[N], ans;
inline void Prim() {
    dis[1] = 0; vis[1] = 1; ans = 0; // 记录距离，以及是否在点集里
    dis[0] = 1e9; // 方便后面的处理
    for(int i = 2; i <= n; i++) dis[i] = 1e9;
    for(int i = G.head(1); i; i = G.nt(i)) {
        dis[G.to(i)] = G.wt(i);
    }
    for(int i = 1; i < n; i++) { // 这里代表要扩张 n-1 次
        int mi = 0; // 找到最短的路径
        for(int j = 1; j <= n; j++) {
            if(!vis[j] && dis[mi] > dis[j]) mi = j;
            // 必须选择未选择的点经行扩张
        }
        vis[mi] = 1; // 他是最小的，纳入点集
        ans += dis[mi];
        for(int j = G.head(mi); j; j = G.nt(j)) {
            int v = G.to(j);
            if(!vis[v] && dis[v] > G.wt(j)) {
                dis[v] = G.wt(j);
            }
        }
    }
    printf("%d\n", ans);
}

然后这样要优化的话，也非常简单，依照 Dijstra 的方式优化即可，也就是用堆，优化掉求最小值的部分等。代码绝对不难写，留给读者。那么那个代码写出来的结果的话，一般来讲的复杂度就是 $O((n+m)\log m)$ ，其中 $n$ 为节点数， $m$ 为边的数量，不难发现，这个算法在对于稠密图的时候非常吃亏，因为稠密图的时候，$m$ 就将近与 $n^2$ 了，这样再加上一个 $n$ 复杂度绝对的爆炸存在。

边贪心：割舍封闭之心

其次又是万众瞩目的 Kruscal 算法。Kruscal 算法的优点在于，代码简短，复杂度相较于 Prim 略优。他被称为边贪心的原因也是因为他的思路，可是他的思路与刚刚的 Prim 恰恰相反。首先我们需要知道一个定理：

一个图中最短的边（如果唯一）一定在最小生成树中。

那么我们的发明者就开始想了，一共就只有 $n-1$ 条边，那么我是不是选出来 $n-1$ 条最短的边就可以了？不然。因为试想一下，如果我们 $n-1$ 条最短的边无法把 $n$ 个点连通，自然称不上最小生成树，也就是说，我们要在满足联通的情况下，尽可能地边权小。

那么想法也很简单，我们直接对于边权排序，每次合并一条最短的，两个端点原来不连通的相连通。这样合并 $n-1$ 次，就是最小生成树。而这个未选点的判定，不难就想到用并查集。因为所谓原来不连通，是因为我们每次只挑最短的边，并不能保证顺序，也就是说，在合并结束前，我们的图一直处于四分五裂的状态。从来都不完整，这时候用并查集判断是不是在同一个连通块，再合适不过。

代码的话，我愿称之为这几个算法中最好写的：

int fa[N];
int find(int x) { return (fa[x] == x ? x : fa[x] = find(fa[x])); }

struct Edge {
    int u, v, w;
}e[M];

inline int Kruscal() {
    int ans = 0, cnt = 0;
    for(int i = 1; i <= n; i++) fa[i] = i;
    sort(e + 1, e + m + 1, [](Edge a, Edge b) {
       	return a.w < b.w; 
    });
    for(int i = 1; i <= m; i++) {
        int u = find(e[i].u);
        int v = find(e[i].v);
        if(u == v) continue;
        ans += e[i].w;
        fa[u] = v;
        cnt++;
        if(cnt == n - 1) break;
    }
    return ans;
}