算法简介：号 · 仙蕊玲珑

这篇文章就是继二维数点里挖下的坑的扫描线内容了。对于扫描线问题，其实是非常广泛的，就像动态规划一样。他主要是提供了一个在二维平面上用平行于坐标轴的线一个一个扫描过来的思想。总归一句话：只有你想不到，没有你扫不到。

友情链接：

【算法介绍】二维数点 | 祝馀宫

只要你可以按照题目的意思建立出可以通过题目的坐标系和线段，使其可以用扫描线扫出来，那么它就是可以的！

算法思想：武 · 西风长枪

首先，既然叫做扫描线，那么上面叫做扫描呢？顾名思义，扫描扫描，从下到上扫一遍就可以了，但是扫描线其实还有一个特点，扫描线。其实所谓扫描线思想，就是把问题转化成一些线段，去按照某个顺序扫描他，然后顺便处理出问题。

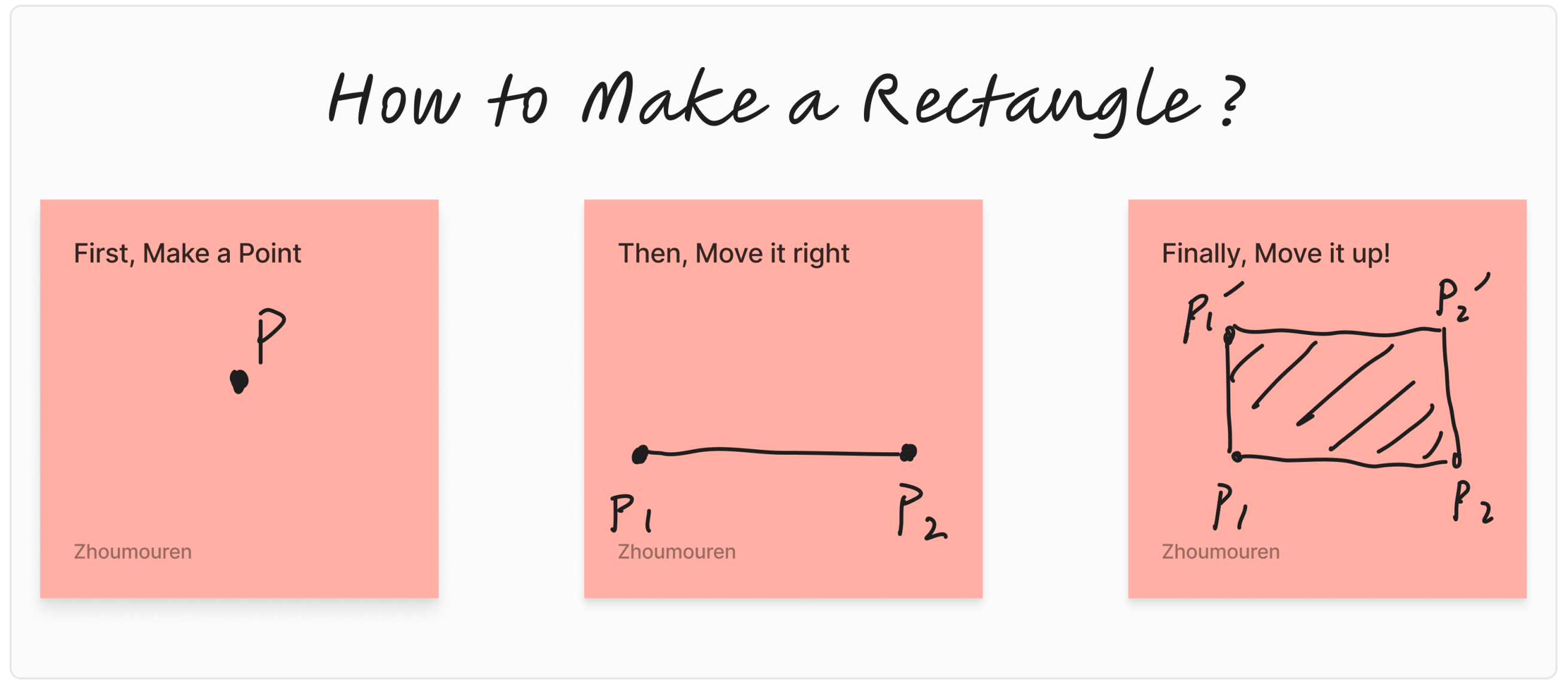
我们可以先给出一个扫描线的经典问题，求矩形面积并。所谓矩形面积并，就是一堆矩形叠在一起，重复覆盖的地方只算一次，当然只出现一次的也是算一次（

那么这题首先第一眼应该都是暴力，毕竟大家都没什么好的思路去做这样奇怪的题目，那么，如果是扫描线呢？他其实是可以做出这样的题目的。为什么，我们来想想矩形是什么。小学大家就学过老师的名言：点动成线，线动成面。其实矩形的本质，就是一个线段，沿着垂直于他自己的方向移动了若干距离，得到的图形。

动态角度理解矩形

那么我们回顾了动态建立矩形的思想。就会发现，做扫描线的过程，不也是一个一个扫描来的吗？一个矩形，其实对应的是线段 $P_1P_2$ 的一个上界和下限。那么想要用扫描线来做出这道题，我们不难有这样的猜想：

扫描线求矩阵面积并

是吧，这就是所谓扫描线的思想，我们会发现，每次遇到一个矩形的下边界，我们目前扫过来的面积长度就会增加，而每次遇到一个矩阵的上边界，扫过来的面积长度就会减少。看到下面的 cnt 了没，这个计数器的作用，是看每一个 x 坐标被覆盖的次数。如果我们遇到一个下边界在对应位置 +1，上边界就 -1 的话。其实面积就变成了：整个 cnt 数组中非 0 的数量 $\times$ 和上一个边界的距离。

然后的话，其实就已经很明显了，由于不可以快速区间加和区间减，于是用线段树解决，然后就完事了。

算法实现：花 · 深林记忆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
// Copied from NCC79601(LuoguUid: 60258)
//  code for P5490
//  代码没有挖坑
#include <stdio.h>
#include <iostream>
#include <algorithm>
#define lson (x << 1)
#define rson (x << 1 | 1)
using namespace std;
const int MAXN = 1e6 + 10;
typedef long long ll;

int n, cnt = 0;
ll x1, y1, x2, y2, X[MAXN << 1];

struct ScanLine {
	ll l, r, h;
	int mark;
//  mark用于保存权值 (1 / -1)
	bool operator < (const ScanLine &rhs) const {
		return h < rhs.h;
	}
} line[MAXN << 1];

struct SegTree {
	int l, r, sum;
	ll len;
//  sum: 被完全覆盖的次数；
//  len: 区间内被截的长度。
} tree[MAXN << 2];

void build_tree(int x, int l, int r) {
//  我觉得最不容易写错的一种建树方法
	tree[x].l = l, tree[x].r = r;
	tree[x].len = 0;
	tree[x].sum = 0;
	if(l == r)
		return;
	int mid = (l + r) >> 1;
	build_tree(lson, l, mid);
	build_tree(rson, mid + 1, r);
	return;
}

void pushup(int x) {
	int l = tree[x].l, r = tree[x].r;
	if(tree[x].sum /* 也就是说被覆盖过 */ )
		tree[x].len = X[r + 1] - X[l];
//      更新长度        
	else
		tree[x].len = tree[lson].len + tree[rson].len;
//      合并儿子信息
}

void edit_tree(int x, ll L, ll R, int c) {
	int l = tree[x].l, r = tree[x].r;
//  注意，l、r和L、R的意义完全不同
//  l、r表示这个节点管辖的下标范围
//  而L、R则表示需要修改的真实区间
	if(X[r + 1] <= L || R <= X[l])
		return;
//  这里加等号的原因：
//  假设现在考虑 [2,5], [5,8] 两条线段，要修改 [1,5] 区间的sum
//  很明显，虽然5在这个区间内，[5,8] 却并不是我们希望修改的线段
//  所以总结一下，就加上了等号
	if(L <= X[l] && X[r + 1] <= R) {
		tree[x].sum += c;
		pushup(x);
		return;
	}
	edit_tree(lson, L, R, c);
	edit_tree(rson, L, R, c);
	pushup(x);
}

int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) {
		scanf("%lli %lli %lli %lli", &x1, &y1, &x2, &y2);
		X[2 * i - 1] = x1, X[2 * i] = x2;
		line[2 * i - 1] = (ScanLine) {x1, x2, y1, 1};
		line[2 * i] = (ScanLine) {x1, x2, y2, -1};
//      一条线段含两个端点，一个矩形的上下边都需要扫描线扫过
	}
	n <<= 1;
//  直接把 n <<= 1 方便操作
	sort(line + 1, line + n + 1);
	sort(X + 1, X + n + 1);
	int tot = unique(X + 1, X + n + 1) - X - 1;
//  去重最简单的方法：使用unique！（在<algorithm>库中）
	build_tree(1, 1, tot - 1);
//  为什么是 tot - 1 ：
//  因为右端点的对应关系已经被篡改了嘛…
//  [1, tot - 1]描述的就是[X[1], X[tot]]
	ll ans = 0;
	for(int i = 1; i < n /* 最后一条边是不用管的 */ ; i++) {
		edit_tree(1, line[i].l, line[i].r, line[i].mark);
//      先把扫描线信息导入线段树
		ans += tree[1].len * (line[i + 1].h - line[i].h);
//      然后统计面积
	}
	printf("%lli", ans);
	return 0;
}

例题讲解：辅 · 团团降芦

那么又到了经典的例题讲解了，早在二维数点里面我就说过扫描线可以做二维数点问题，那么我们就来看一道例题：POJ2482 - 你窗前的星星

Fleeting time does not blur my memory of you. Can it really be 4 years since I first saw you? I still remember, vividly, on the beautiful Zhuhai Campus, 4 years ago, from the moment I saw you smile, as you were walking out of the classroom and turned your head back, with the soft sunset glow shining on your rosy cheek, I knew, I knew that I was already drunk on you. Then, after several months’ observation and prying, your grace and your wisdom, your attitude to life and your aspiration for future were all strongly impressed on my memory. You were the glamorous and sunny girl whom I always dream of to share the rest of my life with. Alas, actually you were far beyond my wildest dreams and I had no idea about how to bridge that gulf between you and me. So I schemed nothing but to wait, to wait for an appropriate opportunity. Till now — the arrival of graduation, I realize I am such an idiot that one should create the opportunity and seize it instead of just waiting.

These days, having parted with friends, roommates and classmates one after another, I still cannot believe the fact that after waving hands, these familiar faces will soon vanish from our life and become no more than a memory. I will move out from school tomorrow. And you are planning to fly far far away, to pursue your future and fulfill your dreams. Perhaps we will not meet each other any more if without fate and luck. So tonight, I was wandering around your dormitory building hoping to meet you there by chance. But contradictorily, your appearance must quicken my heartbeat and my clumsy tongue might be not able to belch out a word. I cannot remember how many times I have passed your dormitory building both in Zhuhai and Guangzhou, and each time aspired to see you appear in the balcony or your silhouette that cast on the window. I cannot remember how many times this idea comes to my mind: call her out to have dinner or at least a conversation. But each time, thinking of your excellence and my commonness, the predominance of timidity over courage drove me leave silently.

Graduation, means the end of life in university, the end of these glorious, romantic years. Your lovely smile which is my original incentive to work hard and this unrequited love will be both sealed as a memory in the deep of my heart and my mind. Graduation, also means a start of new life, a footprint on the way to bright prospect. I truly hope you will be happy everyday abroad and everything goes well. Meanwhile, I will try to get out from puerility and become more sophisticated. To pursue my own love and happiness here in reality will be my ideal I never desert.

Farewell, my princess!

If someday, somewhere, we have a chance to gather, even as gray-haired man and woman, at that time, I hope we can be good friends to share this memory proudly to relight the youthful and joyful emotions. If this chance never comes, I wish I were the stars in the sky and twinkling in your window, to bless you far away, as friends, to accompany you every night, sharing the sweet dreams or going through the nightmares together.

—— 摘自 POJ2482 - Stars in Your Window 题目背景

上面只有题目背景，别妄想在上面找到任何关于题目的信息（/yx

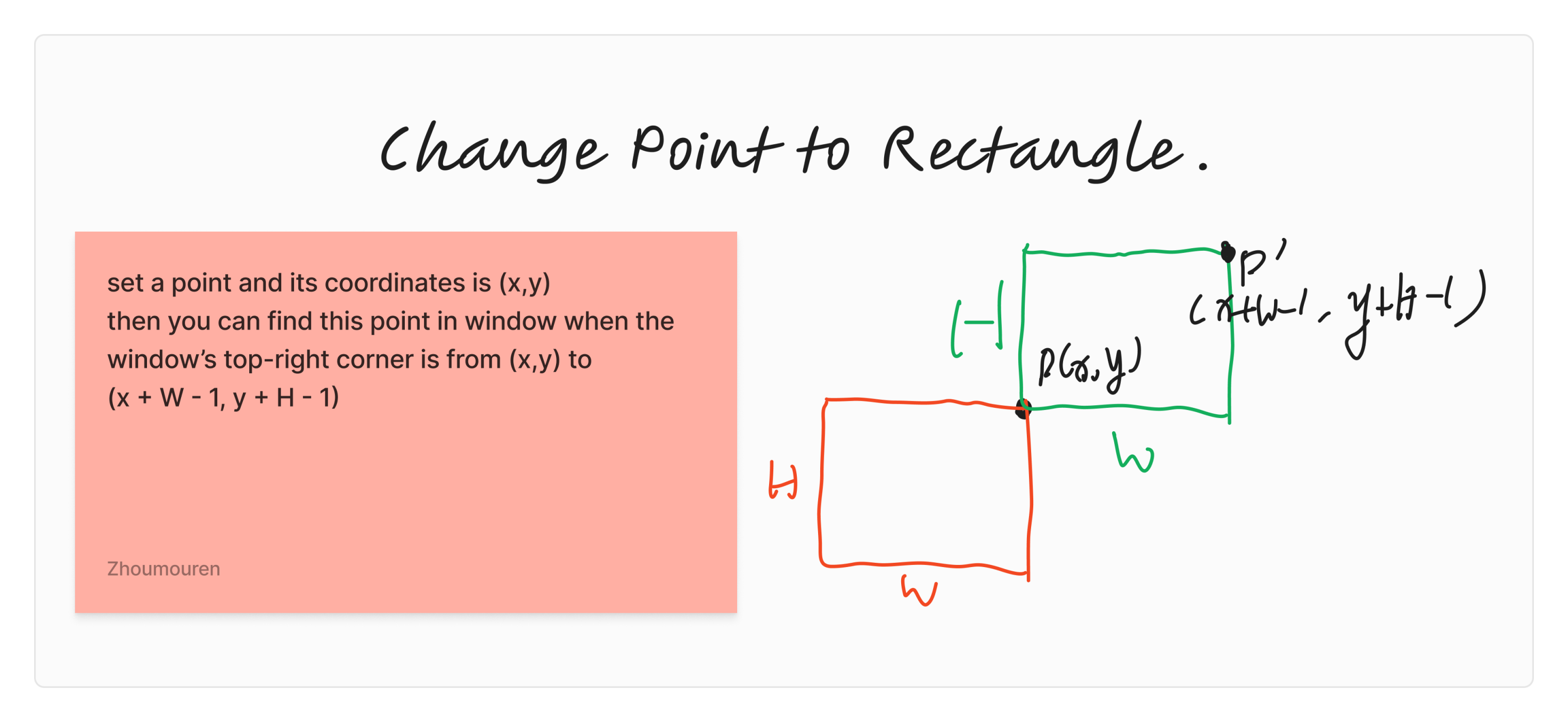
题目意思很简单，就是让你用一个 $W\times H$ （横向长度为 W 纵向长度为 H）的矩形，框住若干个星星，每个星星有亮度，就是让你求框住星星的亮度总和最大值。

有的人就开始说了：哎呀哎呀，刚刚是矩形还可以理解，你现在框的是点哎，怎么能用扫描线呢？你好像连线段都画不出来吧~

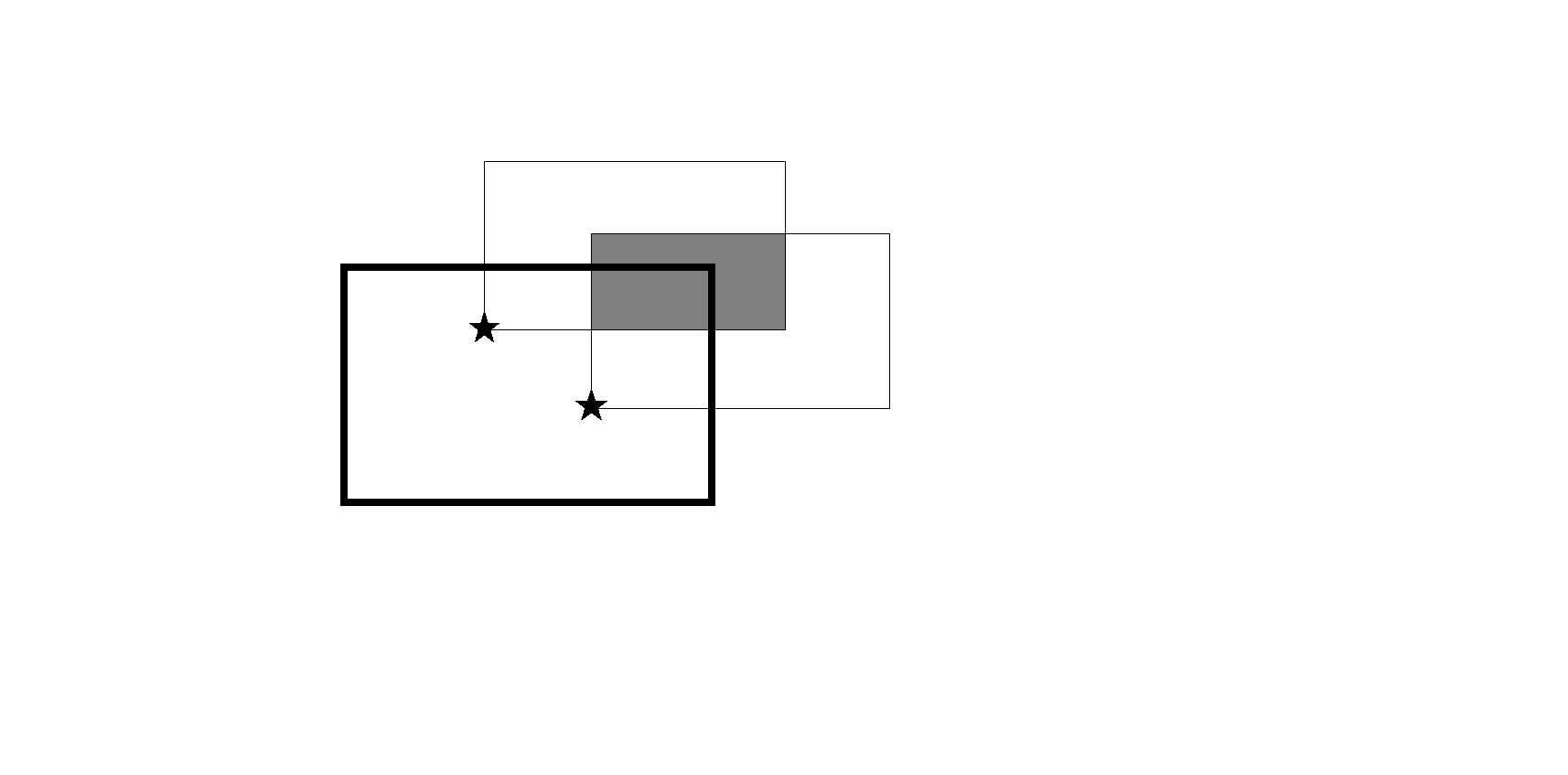
若至。虽然，单独的点不可以找到一个矩形或者线段来代表他。但是，你可以知道一个点在某一个范围是可以被选中的，那你不是就能构造出一个矩形了吗？大概就是下面这样：

矩形框点

那么这个的意义是什么呢？如果我们规定了一个矩形的右上角作为对比符，以此来判定一个矩形的话，那么只要有一个矩形的右上角位于 $(x,y)\sim (x+W-1,y+H-1)$ 那么他就可以把位于 $(x,y)$ 的点框住。那么把每一个点都扩大成一个一个矩形时，如果有重叠的矩形，就意味着位于这块重叠区域的矩形可以同时覆盖两个点。

重叠矩形图示

这就是这题转化的思想了，那么实现也简单了就。

规定矩形的下边界是 +c（ c 为这个矩形对应星星的亮度）上边界是 -c ，那么就可以得到一堆线段等待我们扫描，然后就按照扫描线的思路模拟即可。

例题代码：漫 · 珊珊月落

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
// typedef __int128 int128;
typedef pair<int , int > pii;
typedef unsigned long long ull;

namespace FastIO 
{
    // char buf[1 << 20], *p1, *p2;
    // #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2) ? EOF : *p1++)
    template<typename T> inline T read(T& x) {
        x = 0;
        int f = 1;
        char ch;
        while (!isdigit(ch = getchar())) if (ch == '-') f = -1;
        while (isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
        x *= f;
        return x;
    }
    template<typename T, typename... Args> inline void read(T& x, Args &...x_) {
        read(x);
        read(x_...);
        return;
    }
    inline ll read() {
        ll x;
        read(x);
        return x;
    }
};
using namespace FastIO;

const int N = 1e4 + 10;

int n, W, H;
struct Star {
    ll x, y, c;
}a[N];

inline void Input() {
    if(~scanf("%d", &n)) { }
    else { return exit(0); }
    read(W, H);
    for(int i = 1; i <= n; i++) {
        read(a[i].x, a[i].y, a[i].c);
    }
}

vector<ll >pos;
struct Seg {
    ll ax, ay, bx, by, c;
    Seg() {}
    Seg(ll ax, ll ay, ll bx, ll by, ll c) :
        ax(ax), ay(ay), bx(bx), by(by), c(c) {}
    bool operator < (const Seg & b) const {
        return ay < b.ay;
    }
};
vector<Seg >vec;

inline void Init() {
    for(int i = 1; i <= n; i++) {
        vec.push_back(Seg(a[i].x, a[i].y, a[i].x + W - 1, a[i].y, a[i].c));
        vec.push_back(Seg(a[i].x, a[i].y + H, a[i].x + W - 1, a[i].y + H, -a[i].c));
        pos.push_back(a[i].x), pos.push_back(a[i].x + W - 1);
        pos.push_back(a[i].y), pos.push_back(a[i].y + H);
    }
    sort(pos.begin(), pos.end());
    pos.erase(unique(pos.begin(), pos.end()), pos.end());
    // for(auto &p : pos) cout << p << ' ';
    // cout << endl;
    for(auto &p : vec) {
        // cout << p.ax << ' ' << p.ay << ' ' << p.bx << ' ' << p.by << ' ' << p.c << endl;
        p.ax = lower_bound(pos.begin(), pos.end(), p.ax) - pos.begin() + 1;
        p.ay = lower_bound(pos.begin(), pos.end(), p.ay) - pos.begin() + 1;
        p.bx = lower_bound(pos.begin(), pos.end(), p.bx) - pos.begin() + 1;
        p.by = lower_bound(pos.begin(), pos.end(), p.by) - pos.begin() + 1;
    }
    sort(vec.begin(), vec.end());
}

struct Node {
    // some basic viariables
    ll mx;
    Node() { mx = 0; }
    Node operator + (const Node& b) const {
        Node ans; ans.mx = max(mx, b.mx); return ans;
    }
};
template<const int N>
class SegTree {
private: 
    Node node[N];
    int lc[N], rc[N], cntn;
    ll lazy[N];
public :
    // clear function
    void clear(int rt) {
        if(!rt) return ;
        lazy[rt] = 0, node[rt] = Node();
        clear(lc[rt]);
        clear(rc[rt]);
        lc[rt] = rc[rt] = 0;
    }
    inline int newNode() {
        cntn++;
        lc[cntn] = rc[cntn] = lazy[cntn] = 0;
        return cntn;
    }
    // AddOperation    now   nowl   nowr  addval
    inline void Add(int rt, int l, int r, ll val) {
        node[rt].mx += val;
        lazy[rt] += val;
    }
    // PushDownOperation    now   nowl   nowr
    inline void PushDown(int rt, int l, int r) {
        if(l == r || !lazy[rt]) return ;
        int mid = (l + r) >> 1;
        if(!lc[rt]) lc[rt] = newNode();
        Add(lc[rt], l, mid, lazy[rt]);
        if(!rc[rt]) rc[rt] = newNode();
        Add(rc[rt], mid + 1, r, lazy[rt]);
        lazy[rt] = 0;
    }
    // range Modify now   nowl   nowr   qizl   qizr   addval
    void Modify(int &rt, int l, int r, int L, int R, ll val) {
        if(!rt) rt = newNode();
        if(L <= l && r <= R) {
            Add(rt, l, r, val);
            return;
        }
        PushDown(rt, l, r);
        int mid = (l + r) >> 1;
        if(L <= mid) Modify(lc[rt], l, mid, L, R, val);
        if(R > mid) Modify(rc[rt], mid + 1, r, L, R, val);
        node[rt] = node[lc[rt]] + node[rc[rt]];
    }
    // range Query now   nowl   nowr   qizl   qizr
    Node Query(int &rt, int l, int r, int L, int R) {
        if(!rt) rt = newNode();
        if(L <= l && r <= R) return node[rt];
        PushDown(rt, l, r);
        int mid = (l + r) >> 1;
        Node res; 
        // set some basic value for res
        res.mx = 0;
        if(L <= mid) res = res + Query(lc[rt], l, mid, L, R);
        if(R > mid) res = res + Query(rc[rt], mid + 1, r, L, R);
        return res;
    }
};

SegTree< (N << 2) << 5 > Tree; int rt;

inline void Work() {
    Init();
    ll ans = 0;
    for(int i = 0, len = vec.size(); i < len; i++) {
        // cout << vec[i].ax << ' ' << vec[i].ay << ' ' << vec[i].c << endl;
        Tree.Modify(rt, 1, pos.size(), vec[i].ax, vec[i].bx, vec[i].c);
        if(vec[i + 1].ay != vec[i].ay) {
            ans = max(ans, Tree.Query(rt, 1, pos.size(), 1, pos.size()).mx);
        }
    }
    printf("%lld\n", ans);
}

inline void Clear() {
    pos.clear(), vec.clear();
    Tree.clear(rt), rt = 0;
}

int main() {
    int T = -1;
    while(T--) {
        Clear();
        Input();
        Work();
    }
    return 0;
}

算法实战：性 · 积极好学

查看相关算法标签喵！

参考资料（以下排名不分先后）：

  1. 扫描线 - OI Wiki
  2. 【学习笔记】扫描线 - 洛谷专栏
  3. 题解 P1502 【窗口的星星】 - 洛谷专栏