算法简介：幽邃鸦眼

首先说呢，这个拓展 KMP 其实和 KMP 关系不算特别大。我们定义了一个函数 $\operatorname Z(i)$ 表示字符串 $s$ 中 $s[1\dots n]$ 和字符串 $s[i\dots n]$ 的最长公共前缀的长度，这个函数被叫做 $\operatorname Z$ 函数，由于其代码实现相似于 KMP 算法，于是呢这个算法在国内被称为拓展KMP也就是说本名 $\operatorname Z$ 函数，小名拓展 KMP 。

算法演示：圣裁影羽

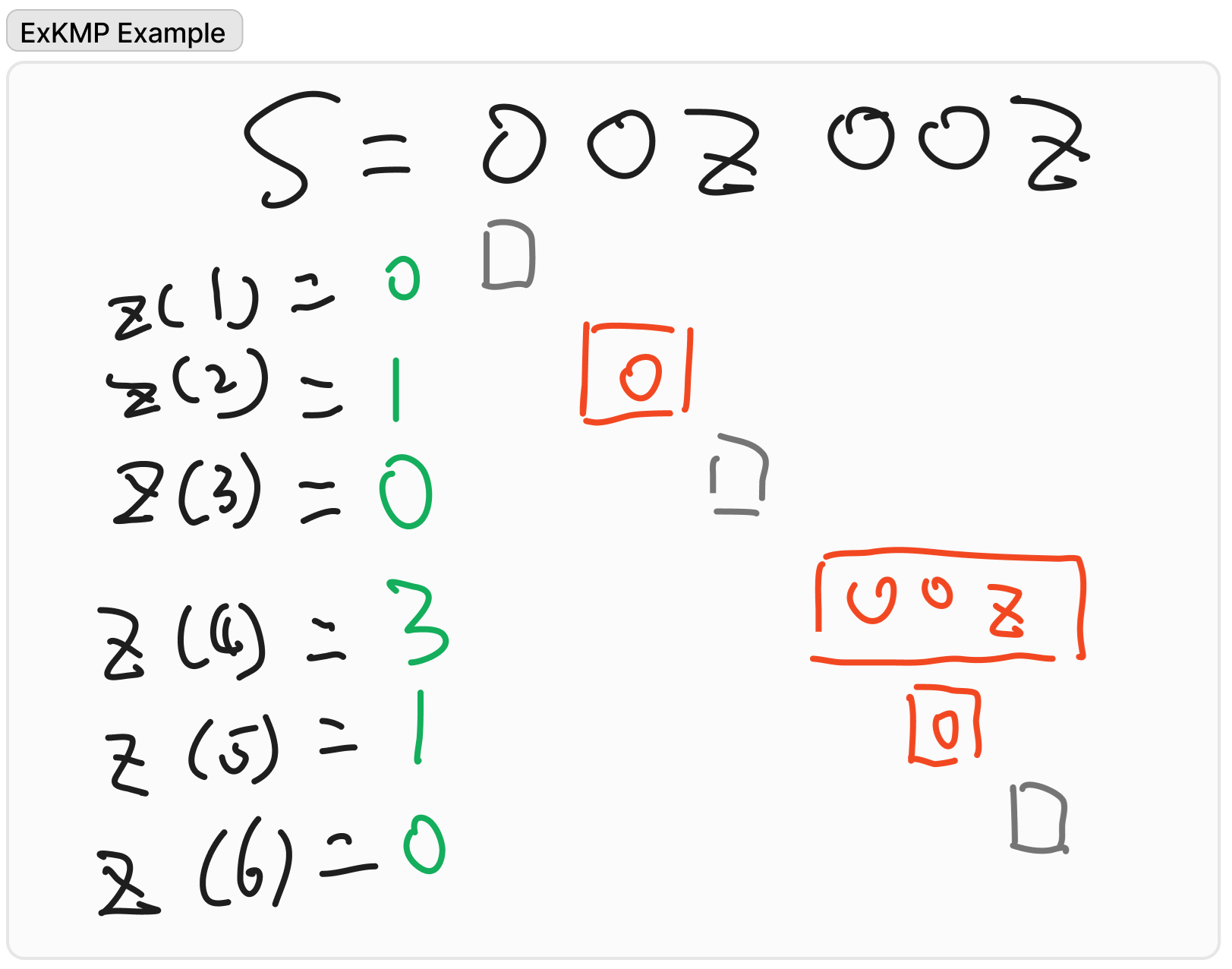
那么首先的首先，我们要知道一个新的算法怎么做，我们肯定是从他的定义出发来看看暴力是怎么样的。那么说我们已经在简介中给出了 $\operatorname Z$ 函数的定义：函数 $\operatorname Z(i)$ 表示字符串 $s$ 中 $s[1\dots n]$ 和字符串 $s[i\dots n]$ 的最长公共前缀的长度。我们可以给出一个例子尝试一下。哦对了我们有一个特殊值 $\operatorname Z(1)=0$ 就是说原字符串和原字符串的最长公共前缀长度，本来说应该是 $n$ 的，但是被特殊定义成了 $0$ 。

函数值：$\operatorname Z(i)$	对应含义
$\operatorname Z(1)=0$	特殊定义的值，不论字符串是什么。这个例子中我们姑且把字符串设为 $s=\tt ozozoozzo$
$\operatorname Z(2)=0$	根据定义，我们要比较原串与 $s[2\dots n]=\tt zozoozzo$，显然没有公共前缀，所以说函数值为 $0$
$\operatorname Z(3)=3$	同样，我们要比较原串与 $s[3\dots n]=\tt ozoozzo$，公共前缀为 $\tt ozo$，长度为 $3$ 。
$\operatorname Z(4)=0$	原串与 $\tt zoozzo$
…	自己找去

OK，那么暴力代码显而易见，我们完全可以用一个 $O(n^2)$ 的代码暴力比对：

inline void ExKMP() {
    z[1] = 0; n = strlen(s + 1);
    for(int i = 2; i <= n; i++) {
        z[i] = 0;
        while(i + z[i] <= n && s[1 + z[i]] == s[i + z[i]]) 
            z[i]++;
    }
}

有了暴力代码，我们要开始考虑优化了。

算法优化：渊色黑翼

那么其实和 KMP 一样，字符串匹配的优化本质，就是用已知信息求出未知信息，有点像动态规划。而在 KMP 中我们使用了一个 nxt 数组加速了计算的过程，拓展 KMP 可以吗？答案显然，不然我们怎么把 $O(n^2)$ 优化到 $\log$ 甚至是线性呢。

还是一样的，就像 KMP ，nxt 表示最长 border 两个 border 是完全一样的。在拓展KMP中，我们也要抓住完全一样的字符串来快速比对，而拓展KMP求的是最长公共前缀，也就是说我们如果存在一个 $\operatorname Z$ 函数 $\operatorname Z(i)$，字符串 $s$ 和字符串 $s[i\dots n]$ 一定存在一个公共子串 $s[i\dots i+\operatorname Z(i)-1]$ ，然后对于这个公共子串，我们可以画图来看看规律：

看见 $\operatorname Z(4)$ 和 $\operatorname Z(5)$ 的关系没有，包含关系。也就是说，如果我们存在了一个被完全覆盖的段，就可以直接从它身上找到答案，但是不呢？我们似乎也没有别的方法，就暂时用暴力填充罢。你那么就有了如下的求拓展KMP的流程。

维护一个右端点最靠右的匹配段，设它的左右端点分别为 $l,r$（因为右端点越靠右越能覆盖后面的段）
对于当前要计算的 $i$ :
- $i\le r$
  - 这时候我们要求的是 $s[i\dots r]$ 他一定是 $s[1\dots r-l+1]$ 的一个后缀，那么我们就会有这样一个式子 $s[i\dots r]=s[i-l+1\dots r-l+1]$ ，那么这时候 $\operatorname Z(i)=\operatorname{max}(\operatorname Z(i-l+1),r-i+1)$
  - 如果 $\operatorname Z(i-l+1)\lt r-i+1$ 说明这次的串被完全包含，直接让 $\operatorname Z(i)=\operatorname Z(i-l+1)$ 就可以
  - 但是如果反过来 $\operatorname Z(i-l+1)\ge r-i+1$，那么就是说我们会有一边的字符串触到底，我们也不知道能不能往右拓展，于是乎我们用暴力往右拓展
- $i\gt r$
  - 我们没有任何可用性息，直接暴力
更新最靠右的匹配段

那么这样的复杂度为多少呢？显而易见的这个复杂度应该是 $O(n)$ 我们会发现右端点最靠右的匹配段只会一去不复返，而如果最靠右的匹配段顶到了头，我们也不会继续暴力，这样的复杂度就是 $O(n)$ 的。

算法模板：皇女绮谭

按照刚刚的思路模拟：

inline void ExKMP() {
    int n = strlen(s + 1);
    for(int i = 2, l = 0, r = 0; i <= n; i++) {
        if(i <= r && z[i - l + 1] < r - i + 1) {
            z[i] = z[i - l + 1];
        }
        else {
            z[i] = max(0, r - i + 1);
            while(i + z[i] <= n && s[1 + z[i]] == s[i + z[i]])
                z[i]++;
        }
        if(i + z[i] - 1 > r) {
            l = i, r = i + z[i] - 1;
        }
    }
}

算法拓展：至夜默示

没想到吧，拓展KMP还有拓展！（bushi

这里说的拓展主要是拓展 KMP 的一个大应用，最小表示法。所谓最小表示法，就是找到一个点 $i\ (1\le i\le n)$ 满足字符串 $s[i\dots n] + s[1\dots i-1]$ 字典序最小。

那么我们可以说目前有两个答案，$i, j$ 他们的前 $k$ 个字符一样，那就是说 $s[i\dots i+k-1]=s[j\dots j+k-1]$ 。这时候我们的第 $k + 1$ 个字符不一样了，也就是 $s[i+k]\neq s[j+k]$ 。

不妨先考虑 $s[i+k]>s[j+k]$ 的情况，我们发现起始位置下标 $l$ 满足 $i\le l\le i+k$ 的字符串均不能成为答案。因为对于任意一个字符串 $s[i+p\dots n]$ 一定存在字符串 $s[j+p\dots n]$ 比它更优。

所以我们比较时可以跳过下标 $l\in [i,i+k]$ 直接比较 $s[i+k+1\dots n]$ 这样，我们就完成了对于上文暴力的优化。

inline int Getmi() {
    int i = 1, j = 2, k = 0, len = strlen(s + 1);
    while(i <= len && j <= len && k <= len) {
        if(s[(i + k) % n + 1] == s[(j + k) % n + 1]) k++;
        else {
            if(s[(i + k) % n + 1] > s[(j + k) % n + 1]) i = i + k + 1;
            else j = j + l + 1;
            if(i == j) i++;
            k = 0;
        }
    }
    return min(i, j);
}