算法总览：散勇化晓摸幺鱼

简单的来说，网络流问题，就是给出一张图，图上面有一个起点，被称作“源点”，还有一个终点，被称作“汇点”。而每一条边都有一个容量，超过容量就不可以通过这条边，有时候边还会有费用，通过这条边就需要花费这些费用。最终的目的就是从源点出发，不管你用什么方法走，最终汇集到汇点的流量最大、或者流量最大中的方案中费用最小的等等等等……这类问题，全都被称作为网络流问题或者流量问题，在生活中应该是非常常见的一种问题。

本文内容限定大纲如下：

  1. 网络流整体简介与符号规定
  2. 网络流经典问题类型
  3. 残量网络的定义
  4. 增广路与反向弧
  5. 最大流计算之 $\tt FF$ 方法
  6. 最大流计算之 $\tt EK$ 算法
  7. 最大流计算之 $\tt Dinic$ 算法
  8. 最大流计算之 $\tt Dinic$ 算法优化
  9. 最小割计算之最大流最小割定理
  10. 最小割计算之割集与变种
  11. 费用流计算之算法推导

算法基础：棋秤作枕好入眠

网络流基本概念

OK啊各位，虽然一开始的文章总览提到了网络流问题的基础概念，但是这里还是补充一下详细的定义以及一些符号，不然容易出现认知上的错误。

网络 $\tt network$ 其实是就是一种特殊的有向图，设图 $G=(V,E)$ 是网络，则它有如下特点：

  • $E$ 中每条边 $(u,v)$ 都存在权值“容量 $\tt capacity$”，记作 $c(u,v)$，如果边集合 $E$ 中不存在边 $(u,v)$ 则可以认为这条边的 $c(u,v)=0$ 。
  • $V$ 中存在两个特殊点：$s$ 源点 $\tt source$，$t$ 汇点 $\tt sink$ 。

对于一个网络 $G=(V,E)$，流 $\tt flow$ 定义为边集 $E$ 映射到实数集的函数，例如边 $(u,v)\in E$ 就有 $f(u,v)$ 表示这条边的流量，则对于这个函数我们有如下的性质：

  1. 容量限制：$\forall (u,v)\in E$ 都有 $0\le f(u,v)\le c(u,v)$ 即流量不可超过容量。
  2. 流守恒性：对于除了源点 $S$ 和汇点 $T$ 以外的所有点，其净流量都为 $0$ 。其中，我们定义结点 $u$ 的净流量为 $f(u)=\sum_{x\in V} f(u,x)-\sum_{x\in V}f(x,u)$，即流出结点 $u$ 的总流量和流入结点 $u$ 的总流量之差。

然后呢对于网络 $G=(V,E)$ 我们定义其流 $f$ 的流量 $|f|=f(s)$ 即源点净流量。我们认为在网络上，所有流量都是由源点产生的，即源点没有流入流量，只有流出流量。那么相反的，汇点的流量$\ f(t)=-f(s)$，这是因为汇点只消耗流量，不流出流量。

网络流经典问题

最大流问题：

给出有源汇点 $s,t$ 的网络 $G=(V,E)$，我们要指定这一整张图的流 $f$，使得在不超过容量（否则这个流无效）的情况下，整张图的流量或者说源点产生的流量最大。

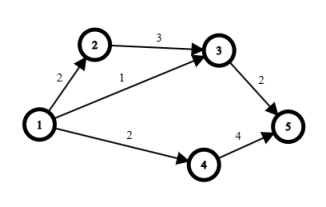
这里要区分“最大流”和“最短路”之类的概念的区别。“最短路”是一种路径，他只有一条，一个起点，一个终点，这条从起点到终点的路径上应该满足每个点只有一个入度一个出度，不然都话这个路径必然存在环，也就不是路径了。而“最大流”是一种流，可以举一个下图这样的例子（下图 $1$ 是源点，$5$ 是汇点，别忘了网络是有向图）

网络流举例

对于这个例子来说，如果你没有理解流的概念你可能会认为这张图的最大流是 $1\rightarrow 4\rightarrow 5$ 或者 $1\rightarrow 2\rightarrow 3\rightarrow 5$ 总而言之错误点认识是最大流是 $2$ 。但是真正的最大流应该是 $4$，先走路径 $1\rightarrow 4\rightarrow 5$ 流掉这两条边 $2$ 的流量，这时候 $(1,4)$ 这条边就用不了了，因为所有的容量 $2$ 已经被用完；然后流路径 $1\rightarrow2\rightarrow3\rightarrow 5$ 流掉这三条边 $2$ 的流量，这时候 $(1,2)$ 和 $(3,5)$ 这两条边也都用不了了，原因同上。这时候剩下的图的流量都已经不支持在进行一次流，所以源点 $1$ 产生的总流量应该是 $2+2=4$ 。

上面举例的流其实也还都是路径，你甚至可以做出这样一个流，源点 $1$ 向 $2,3$ 点分别产生 $1$ 的流量，然后 $2$ 点流量留到 $3$ 点以后，与 $3$ 点本身的 $1$ 流量合并为 $2$ 流量，流到汇点 $5$ 消耗。也就是说流也是可以有分支的，这是一个非常有趣的例子。

最小割问题：

首先给出割的定义，我们把网络 $G=(V,E)$ 划分为集合 $S,T$，其中满足 $T=V-S$ 即满足 $S\cup T=V,S\cap T=\varnothing$，其中有一个要求源点 $s\in S$，汇点 $t\in T$。

然后给出割的容量的概念。对于一组割 $(S,T)$，我们定义它的容量为 $c(S,T)$ 表示 $S$ 和 $T$ 之间的边的容量之和，即 $\sum_{u\in S,v\in T}c(u,v)$。另外我们也可以用 $c(s,t)$ 来表示 $c(S,T)$ 其中 $s,t$ 为网络的源点和汇点。

那么最小割其实就是找到一组割 $(S,T)$，使得 $c(S,T)$ 最小。

这个问题乍一眼很难搞，但是实际上是一个特别有意思的问题，题目的基本定义就放在这里了，先不透露具体解决这个问题的方案。

费用流问题：

给定网络 $G=(V,E)$，每条边除了容量以外现在额外增加新的概念 “费用” $w(u,v)$。这个费用指的是这条边每经过一的流量就要支付一个 “费用”，即最终当 $(u,v)$ 的流量为 $f(u,v)$ 时，所需支付的费用就是 $f(u,v)\times w(u,v)$ 。另外 $w$ 满足斜对称性，即 $w(u,v)=-w(v,u)$，这个性质是一会要介绍的，所以先记着。

那么费用流问题中最经典的就是网络中总花费最小的最大流，即最小费用最大流，即最大化 $|f|$ 的前提下最小化总花费 $\sum_{(u,v)\in E}f(u,v)\times w(u,v)$。

这个问题一眼看上去就和最大流有着不小的渊源，确实也的确如此。这就是网络流最基础的一些问题，接下来就是一些解决这些问题要用到的前置知识了。

流后的残量网络

残量网络是处理网络流问题的重要概念。大概就是对于容量为 $c$ 的边，我们知道容量用一点少一点，鱼逝对于一个使用了 $c’$ 容量的边，将其容量减去 $c’$，并建立起一条边权为 $c’$ 的反向边。

形式化的来讲，残量网络设为有向图 $G’=(V,E’)$，则边集 $E’$ 中存在边：

并且定义关于边集合 $E’$ 的容量 $c’$ 为（设原图容量为 $c$ 函数）

呃，有点多此一举

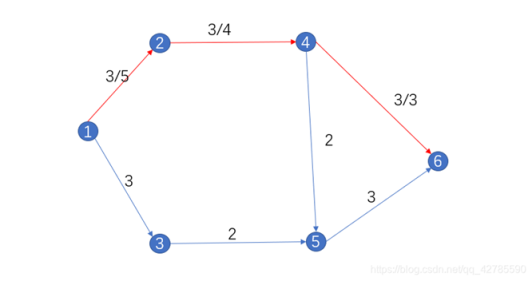
接下来可以适当的看一下，举个例子，下图中红色表示一个流，流掉了 $3$ 的流量， f/c 表示流量/容量。

一个流的实例

那么如果对于这个流画出其对应的残量网络，就是下图这样（容量为零的边被省略了）：

残量网络实例

残量网络就这些东西，然后是增广路与反向弧。

增广路与反向弧

先讲增广路罢，增广路应该是特别熟悉的，我们在二分图中就学过了增广路，其实网络流和二分图有不小的渊源，我们在关于最小割问题的时候就会注意到，这里依然先卖个关子。

增广路呢，就是残量网络上一条从源点到汇点的一条简单路径。就像最上面关于网络流基本问题的最大流中提到的那种简单路径形式的流一样。

网络流举例

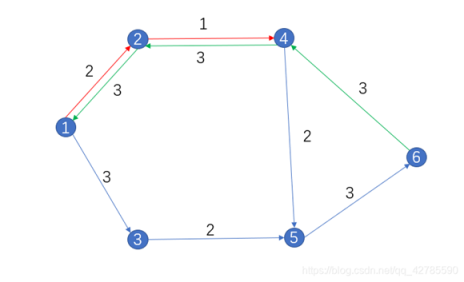
在这个例子中，像路径 $1\rightarrow 2\rightarrow 3\rightarrow 5$ 就是一条关于一个没有流过的参量网络即原图的一条增广路。再比如说下图中，我们流掉了 $1\rightarrow2\rightarrow3\rightarrow4$ 这条增广路上 $1$ 的流量，我们还可以再在这个残量网络上流走 $1\rightarrow3\rightarrow2\rightarrow4$ 这条增广路上 $1$ 的流量。没错，残量网络上反向的这些边也是可以当作增广路路径的一部分的。

其实你肯定也注意到了，其实我们在残量网络上建立的这些与原图相反的边就是我们常说的反向弧，它的作用就会在下一节揭晓~

算法其一：观琼视莹门前清

起初思路：FF 方法

那么 FF 方法，全称 Ford–Fulkerson，就是计算网络最大流的一类算法的统称，接下来的两个算法以及优化都是源自于 FF 方法。关于 FF 方法，其实是一个很好想到的贪心思路。

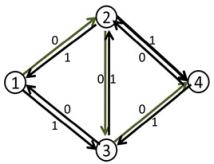
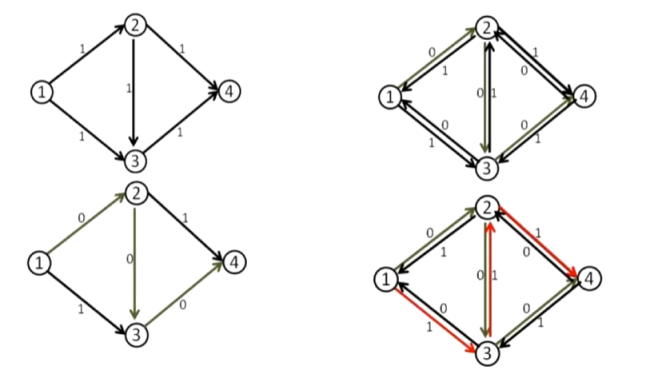
我们就从上面提到的一个非常简单的网络看起：

第一行的第一个是初始的网络，其中源点是 $1$ 汇点是 $4$ 。接下来流走 $1\rightarrow2\rightarrow3\rightarrow4$ 这条增广路，则变成第二行第一个的样子。接下来画出关于它的残量网络，则有第一行第二个这样的图，这时候注意到还有第二行第二个这样红色的增广路。这时候注意到有 $1\rightarrow2\rightarrow4$ 和 $1\rightarrow3\rightarrow4$ 两条流量为一的流，这时候不再存在增广路，同时也“巧合地”成就了这个网络的最大流 $2$ 。

这真的是巧合吗？我们可以很简单的证明出如果一个图还存在增广路，那么就不是最大流，即当前流是最大流的必要条件是不存在增广路。但是充分性如何证明？

必要性证明：显然的，如果残量网络中仍然存在增广路，则就可以启用这条增广路以为了得到更多的流量。

充分性的证明需要用到最小割与一个定理，被称为最大流最小割定理，这个定理的证明被放在了讲解最小割问题转化的部分中，可以先去阅读一下，定理的结论是最大流和最小割相等，这将是证明充分性的重要定理。

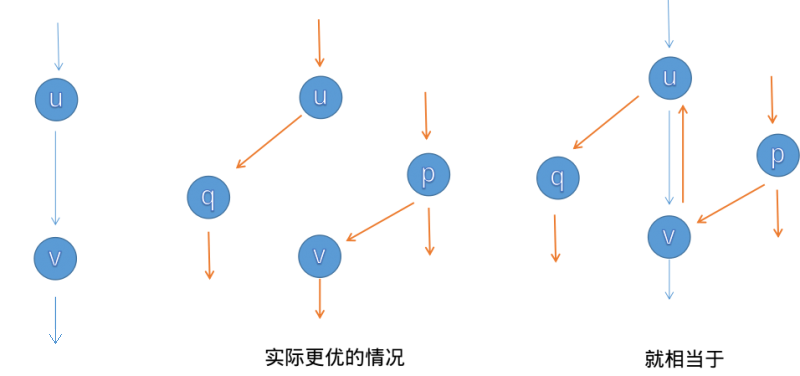
这时候我们就可以注意到反向边的重要性，就比如说下图：

下图中我们已知有一条增广路最左边的，实际的最有情况是中间的，当前的流是最左边的黄色部分。这时候如果我们引入了已知的这条增广路，可以注意到 $(u,v)$ 会抵消掉原来流的那一条边，相当于是返回操作，这样我们就可以不断地增广直到不存在增广路。

这个操作被称为退流操作。那么接下来关于 FF 方法及其衍生算法的优化，其实就在于寻找增广路了，我们大体上可以有如下伪代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int Ford_Fulkerson(G, S, T) {
    for(each edge(u, v, w)) {
        c[u][v] = w, c[v][u] = 0;
        f[u][v] = 0, f[v][u] = 0;
    }
    maxflow = 0;
    while(exists p from S to T in residual network Gf) {
        cf(p) = min{ cf(u, v): (u, v) is in p };
        maxflow += cf(p);
        for(each edge(u, v, w) in p) {
            f[u][v] += cf(p);
            f[v][u] -= cf(p);
        }
    }
    return maxflow;
}

基础版本：EK 算法

EK 算法，全程 Edmonds-Karp 算法，就是上述 FF 方法所对应的最简单暴力的实现方式。我们知道关于实现 FF 方法的区别，其实就是在于找到增广路的过程，而最简单的，就是不断地增广一条增广路，直到不存在增广路。而这个每次增广一条边的增广方式，非常显然的容易想到 BFS，所以关于 EK 算法，我们可以有这样的猜想。

  • 在当前的残量网络 $G_f$ 上从 $s$ 开始 BFS 到 $t$，说明找到了增广路。
  • 假设这条增广路是 $p$，构成这条增广路的边分别是 $(u,v)\in p$，则我们可以从这条增广路上压榨的最大流量，就是整条增广路上剩余容量最小的边，即 $\min_{(u,v)\in p}c_f(u,v)$ 。不妨将其设为 $\Delta$ 。
  • 则根据 FF 方法的思路，我们只要在这些边的流量中增加 $\Delta$ 的流量，在其反向边退掉 $\Delta$ 流量，那么这样就可以令最大流增加 $\Delta$ 流量，非常的完美。
  • 然后就继续在残量网络上面跑这个过程即可。

这就是 Edmonds-Karp 算法，接下来对于这个算法进行复杂度分析。

首先显而易见的，BFS 的复杂度一定是 $O(|E|)$，接下来就是要证明最多会进行几轮 BFS，实际上，进行 BFS 的总轮数应该是 $O(|V||E|)$ 即总复杂度是 $O(|V||E|^2)$，接下来尝试证明一波。

证明：EK 算法中进行 BFS 的总轮数是 $O(|V||E|)$ 轮。

首先证明这个结论需要一个小引理：最短路非递减引理。大概就是设第 $i$ 轮增广后的结果是 $G_f$，第 $i+1$ 轮增广后的结果是 $G_{f’}$，再设 $d_f(u)$ 是 $G_f$ 从 $u$ 点到源点的最短距离，则一定有 $d_{f’}(u)\ge d_f(u)$。

证明：最短路非递减引理

考虑反证。对于某一轮增广，假设存在若干点，他们在增广后到 $s$ 的距离比增广前小了。假设在这些殿中，距离 $s$ 最小的一个点是 $v$，则满足 $d_{f’}(v)<d_f(v)$。

在 $G_{f’}$ 中从 $s$ 到 $v$ 的最短路上设 $u$ 是 $v$ 的直接先驱，即满足 $d_{f’}(u)+1=d_{f’}(v)$。

显然的，$u$ 满足 $d_{f’}(u)\ge d_f(u)$，因为如果 $u$ 是满足增广后距离 $s$ 的距离变小的那一类点，根据定义就有 $d_{f’}(u)<d_f(u)$，而又因为 $d_{f’}(u)+1=d_{f’}(v)$ 这就说明了 $d_{f’}(u)<d_{f’}(v)$，这直接与 $v$ 的定义矛盾了，所以 $d_{f’}(u)\ge d_f(u)$ 。

然后我们可以对于不等式继续推导，$d_{f’}(v)=d_{f’}(u)+1\ge d_f(u)+1$，再联立一开始假设的初始条件 $d_{f’}(v)<d_f(v)$，$d_f(u)+1\le d_{f’}(v)<d_f(v)\Longrightarrow d_f(u)+1<d_f(v)$ 。

有了这个不等式，其实就是让我们考虑在第 $i$ 轮增广结果 $G_f$，也就是 $f’$ 的前一轮增广的增广方向，即边 $(u,v)$ 所属的范围。

  • 假设有向边 $(u,v)\in E_f$，则根据 BFS 的定义“广度优先”，显然的会有 $d_f(u)+1\ge d_f(v)$，这就与上面的推论矛盾，也就是不可能是这种情况。
  • 反过来假设有向边 $(u,v)\notin E_f$，这时候这条边在原来的残量网络 $G_f$ 不存在，也就是说这条边一定是在后一轮增广中通过退流操作建立起来的。那么也就是说在原来的残量网络上存在这条边的反向边即 $(v,u)$，那么我们们有 $d_f(v)+1=d_f(u)$，再次与推论矛盾，也不是这种情况

综上，可以得出结论 $(u,v)$ 不论如何增广都会矛盾，也即是假设不成立，则该引理得证。

那么接下来就是证明 BFS 轮数是 $O(|V||E|)$ 的了。我们设增广路上剩余容量最小的边为饱和边（如有多条任选其一）如果有一条有向边 $(u,v)$ 被选为饱和边，则这条边在增广以后会消耗掉它本身全部的容量并建立起对应的反向边（如果不存在这个反向边），那么显然的对于有向边 $(u,v)$ 它的状态一定是在 $(u,v)$ 和 $(v,u)$ 反复横跳。

那么如果是在残量网络 $G_f$ 上沿 $(u,v)$ 增广时，$d_f(u)+1=d_f(v)$，然后残量网络变为 $G_{f’}$。在 $G_{f’}$ 上沿着反向边 $(v,u)$ 增广时，$d_{f’}(v)+1=d_{f’}(u)$。根据最短路非递减引理又有 $d_{f’}(v)\ge d_f(v)$ 联立所有式子就可以得到 $d_{f’}(u)\ge d_f(u)+2$，也就是说某一条便被选作饱和边后，必然与上一次选做饱和边时 $u,s$ 的距离增加 $2$ 。

这就意味着一条边被选作饱和边的次数上限是 $O(|V|)$ 因为最坏情况下源点到汇点的结构是一条链，每次增加二但是这个小常数直接忽略不计所以算作 $O(|V|)$，接下来由于有 $O(|E|)$ 条边，所以总的次数应该是 $O(|N||E|)$ 范围的。

至此完成了关于 EK 算法的复杂度证明，接下来就是代码实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
constexpr int MAXN = 250;
constexpr int INF = 0x3f3f3f3f;

struct Edge {
  int from, to, cap, flow;

  Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};

struct EK {
  int n, m;             // n：点数，m：边数
  vector<Edge> edges;   // edges：所有边的集合
  vector<int> G[MAXN];  // G：点 x -> x 的所有边在 edges 中的下标
  int a[MAXN], p[MAXN];  // a：点 x -> BFS 过程中最近接近点 x 的边给它的最大流
                         // p：点 x -> BFS 过程中最近接近点 x 的边

  void init(int n) {
    for (int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void AddEdge(int from, int to, int cap) {
    edges.push_back(Edge(from, to, cap, 0));
    edges.push_back(Edge(to, from, 0, 0));
    m = edges.size();
    G[from].push_back(m - 2);
    G[to].push_back(m - 1);
  }

  int Maxflow(int s, int t) {
    int flow = 0;
    for (;;) {
      memset(a, 0, sizeof(a));
      queue<int> Q;
      Q.push(s);
      a[s] = INF;
      while (!Q.empty()) {
        int x = Q.front();
        Q.pop();
        for (int i = 0; i < G[x].size(); i++) {  // 遍历以 x 作为起点的边
          Edge& e = edges[G[x][i]];
          if (!a[e.to] && e.cap > e.flow) {
            p[e.to] = G[x][i];  // G[x][i] 是最近接近点 e.to 的边
            a[e.to] =
                min(a[x], e.cap - e.flow);  // 最近接近点 e.to 的边赋给它的流
            Q.push(e.to);
          }
        }
        if (a[t]) break;  // 如果汇点接受到了流，就退出 BFS
      }
      if (!a[t])
        break;  // 如果汇点没有接受到流，说明源点和汇点不在同一个连通分量上
      for (int u = t; u != s;
           u = edges[p[u]].from) {  // 通过 u 追寻 BFS 过程中 s -> t 的路径
        edges[p[u]].flow += a[t];      // 增加路径上边的 flow 值
        edges[p[u] ^ 1].flow -= a[t];  // 减小反向路径的 flow 值
      }
      flow += a[t];
    }
    return flow;
  }
};

进阶优化：Dinic 算法

显然的，每次更新一条增广路，这么说都有点太少了，所以 Dinic 算法的不同之处，就是多路增广。即一次增广多条边，来处理问题。

那么 Dinic 算法的核心思想，在于利用分层图的思想来寻找一个增广流。所谓增广流，就是我们在这之前的 EK 算法中每次增广的是一条路径，然后这一次我们一次增广一整个流，这就是增广流。关于分层图的话，就是我们把距离源点相同的点放在同一层里，同一层中的结点不能有边相连。

形式化的来讲，我们设当前的残量网络 $G_f=(V,E_f)$ 有层次图 $G_L=(V,E_L)$，那么边集满足 $E_L=\{(u,v)\mid (u,v)\in E_f,d(u)+1=d(v)\}$。

那么接下来就是反复的执行：

  1. 在残量网络 $G_f$ 上寻找层次图 $G_L$ 。
  2. 在层次图上寻找最大的增广流 $f_b$ 。
  3. 合并流 $f_b$ 至答案流 $f$ 。
  4. 重复直至源汇点不连通。

我们就会有这样的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
inline bool DinicBfs() {
	for(int i = 1; i <= n; i++) level[i] = 0;
    level[S] = 1;
    queue<int >q;
    q.push(S);
    while(!q.empty()) {
        int u = q.front(); q.pop();
        for(int i = G.head(u); i; i = G.nt(i)) {
            int v = G.to(i);
            if(level[v]) continue;
            if(G.cap(i) <= G.flw(i)) continue;
            level[v] = level[u] + 1;
            q.push(v);
        }
    }
    return level[T] != 0;
}

inline int DinicDfs(int u, int cp) {
    if(u == T) return cp;
    int tmp = cp;
    for(int i = G.head(u); i && tmp; i = G.nt(i)) {
        int v = G.to(i);
        if(level[u] + 1 == level[v] && G.cap(i) > G.flw(i)) {
            int t = DinicDfs(v, min(tmp, G.cap(i) - G.flw(i)));
            G.flw(i) += t, G.flw(((i-1)^1)+1) -= t;
            tmp -= t;
            if(tmp == 0) break;
        }
    }
    return cp - tmp;
}

inline int Dinic() {
    int flow = 0;
    while(DinicBfs()) {
        flow += DinicDfs(S, INF);
    }
    return flow;
}

最终版本：当前弧优化

上面的版本其实是不够优秀的，我们会注意到在 $G_L$ 上 DFS 的过程中，如果 $u$ 结点有 $n$ 条入边和出边，对于每一次接受入边的流量都需要暴力枚举所有边来决定继续传递，这样的复杂度直接超级加倍到 $O(n^2)$，这样是绝对不允许的。

那么我们就有了一个很好的优化，叫做当前弧优化。具体的来说，我们深搜之后的结果一定把某一个边变为饱和边或增广至阻塞即不可增广（饱和边还是上面 EK 算法里面提到的）总而言之这条边就不能被通过了，所以不必再次走这条边，所以每次记录深搜到哪个边，从他的下一个开始搜索就可以了。

当前弧优化后的 Dinic 算法复杂度就降低到可接受范围内了，不再是 $O($玄学$)\ $的算法，所以这里我们就可以估计复杂度力！

首先一样是推单次增广复杂度。

单次增广复杂度推理

考虑当前最大的增广流 $f_b$ 中的每条增广路，他们一定都是在 $G_L$ 上每次沿着当前弧不停跳转得到的结果，其中每条增广路经历的跳转次数都不可能多于 $|V|$ 。

没找到一条增广路就一定会有一条饱和边消失，这是因为它的剩余容量被清零了。然后对于这些被清零的饱和边建立起一个边集合 $E_1$ 。由于我们设定了 $G_L$ 分层，所以饱和边的反向边不可能被同时增广到，所以 $E_1$ 一定是 $E_L$ 的子集。

另外，对于沿着当前弧跳转，但还是阻塞导致增广不成功的边的最后一边放到集合 $E_2$ 中，$E_2$ 里的边一定不是饱和边，所以 $E_1$ 与 $E_2$ 不相交，并且由于增广范围的限制，$E_1\cup E_2$ 也是 $E_L$ 的子集。

接下来由于 $E_1\cup E_2$ 的每一个元素都没有超过 $|V|$ 次跳转，这是因为 $E_1$ 只会跳转一次就被清零，然后 $E_2$ 由于路径长度限制至多经行 $|V|$ 次，所以总而言之单轮增广的复杂度一定不会超过 $O(|V||E_L|)$ 。

然后我们来看最多进行多少轮增广，其实这里证明最多增广次数是和 EK 一个道理，显然的层次图的最大数量是 $|V|$ 个，所以说如果证明层次图单增，那么就可以计算出进行 $O(|V|)$ 次增广。

证明：层次图的层数在增广过程中严格单调递增。

首先对于层次图的定义做出一点点小改变，现在我们的函数 $d_f(u)$ 定义为 $G_f$ 上结点结点 $u$ 到汇点 $t$ 的距离，分层图变为从汇点出发开始分层，显然的这与源点出发分层并无本质区别。对于某一轮增广，设增广前的流为 $f$ 增广后的流为 $f’$。那么按照 Dinic 算法的流程，把这一轮增广的结果合并到答案里面后，设层次图 $G_L=(V,E_L)$ 变为 $G’_L=(V,E’_L)$ 。

接下来引入概念高度标号的概念，大致含义是在网络 $G=(V,E)$ 上，令函数 $h$ 是点集 $V$ 映射到自然数集 $N$ 的函数，那么 $h$ 是该网络的合法高度标号当且仅当 $h(u)\le h(v)+1$ 对于任意的 $(u,v)\in E$ 恒成立。

接下来考虑增广后的网络（不是层次图）$G_{f’}$ 对应的边集 $E_{f’}$ 的所有元素 $(u,v)$，那么就会分为以下两种可能：

  1. $(u,v)\in E_f$，且剩余容量在该轮增广没有耗尽。这样根据最短路的定义，显然会有 $d_f(u)\le d_f(v)+1$ 。
  2. $(u,v)\not\in E_f$，那么这条边一定是这一次的结果合并过程中退流产生的。根据层次图的定义，这时候我们有等式 $d_f(u)+1=d_f(v)$ 。

那么根据上述的结论，可以看出 $d_f$ 应该是满足高度标号的条件的，即 $d_f$ 是 $G_{f’}$ 上的一个合法标号，那么 $d_f$ 在原图 $G_{f’}$ 上都成立，作为子图的 $G_L’$ 也必然是成立的。

这时候问题就在不知不觉中化简了，对于增广路 $p=(s,\dots,u,v,\dots,t)$，按照新编的从汇点开始到源点的顺序考虑每一个结点加入增广路的过程。设 $v$ 结点已经加入，$u$ 结点正在加入，这时候可以思考 $d_{f’}$ 的变化。加入结点 $u$ 以后，显然的可以根据层次图的定义得到 $d_{f’}(u)=d_{f’}(v)+1$；另外，$d_f$ 是关于 $G_L’$ 的高度标号，那么关于 $d_f(u)$ 的值来说，最多是比 $d_f(v)$ 多一，甚至可以是不变或者减少。所以说我们不难得到 $d_{f’}(s)\ge d_f(s)$ 其中去等的充要条件是 $d_f(u)=d_f(v)+1$ 对于增广路 $p$ 中的每一条边 $(u,v)$ 都成立。

那么我们想要证明的是 $d_{f’}(s)>d_f(s)$ 也就是层数严格单增，就是要求上述取等条件不成立，那么原命题就成立了，接下来就尝试证明无法取等。

考虑反证，假设 $d_{f’}(s)=d_f(s)$ 成立。现在我们断言，在 $G_L’$ 上 $p$ 至少包含一条边满足 $(u,v)$ 在 $G_L$ 上不存在。如果没有这样的边，因为 $d_f(s)=d_{f’}(s)$，根据层次图的定义可以知道增广一定未完成。为了不出现矛盾，我们必须要满足断言成立。

令 $(u,v)$ 是满足断言条件的边，那么它满足断言的原因只能是如下两个中的一个：

  1. $(u,v)\in E_f$ 但 $d_f(u)\le d_f(v)+1$ 未取等，根据层次图的定义可知 $(u,v)\not\in E_L$，并在增广后新的一轮重新分层中被加入到 $E_L’$ 中。
  2. $(u,v)\not\in E_f$，这意味着 $(u,v)$ 这条边是因为退流产生的，也就是 $d_f(u)=d_f(v)-1$ 。

注意到上面的方式都不满足 $d_f(u)=d_f(v)+1$，也就是说 $d_{f’}(s)\ge d_f(s)$ 的取等条件无法满足，这就与一开始的假设冲突了，至此原命题彻底得证。

那么这一轮证明下来，就是说单轮的复杂度 $O(|V||E|)$ 与单增造成的 $O(|V|)$ 次数相乘，就可以得到最终 Dinic 当前弧优化以后的时间复杂度，也就是 $O(|V|^2|E|)$ 。

虽然看上去这个算法的复杂度非常超标，但是呢一般来讲，如果是网络流的题，他不会特意卡 Dinic 算法的。也就是说 Dinic 算法远远达不到这次的时间复杂度上限。一般来讲，Dinic 算法跑 1e4~1e5 范围内的题目都是没有问题的。

那么关于当前弧优化，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
inline bool DinicBfs() {
	for(int i = 1; i <= n; i++) level[i] = 0;
    level[S] = 1;
    queue<int >q;
    q.push(S);
    while(!q.empty()) {
        int u = q.front(); q.pop();
        for(int i = G.head(u); i; i = G.nt(i)) {
            int v = G.to(i);
            if(level[v]) continue;
            if(G.cap(i) <= G.flw(i)) continue;
            level[v] = level[u] + 1;
            q.push(v);
        }
    }
    return level[T] != 0;
}

inline int DinicDfs(int u, int cp) {
    if(u == T) return cp;
    int tmp = cp;
    for(int &i = cur[u]; i && tmp; i = G.nt(i)) {
        int v = G.to(i);
        if(level[u] + 1 == level[v] && G.cap(i) > G.flw(i)) {
            int t = DinicDfs(v, min(tmp, G.cap(i) - G.flw(i)));
            G.flw(i) += t, G.flw(((i-1)^1)+1) -= t;
            tmp -= t;
            if(tmp == 0) break;
        }
    }
    return cp - tmp;
}

inline int Dinic() {
    int flow = 0;
    while(DinicBfs()) {
        for(int i = 1; i <= n; i++) {
            cur[i] = G.head(i);
        }
        flow += DinicDfs(S, INF);
    }
    return flow;
}

算法其二：帝垣翔鳞和绝张

基础推导：定理转化

那么这里的定理，就是被埋了无数次伏笔的定理，最大流最小割定理。那么其内容就是对于任意的网络 $G=(V,E)$ 其最大流 $f$ 和最小割 $\{S,T\}$ 总满足 $|f| = ||S,T||$。

对任意可行流 $f$ 和任意割 $\{S, T\}$，流的值为：

因此，最大流不超过所有割的容量。

假设 $f$ 是最大流，其残留网络 $G_f$ 中无 $s$ 到 $t$ 的路径。令：

  • $S$ ：在 $G_f$ 中从 $s$ 可达的顶点集合。
  • $T = V - S$（显然 $t∈T$）。
  1. 从 $S$ 到 $T$ 的边 $(u, v)$ ：在 $G_f$ 中无正向边（否则 $v∈S$ ），故残留容量 $c_f(u, v) = 0 ⇒ f(u, v) = c(u, v)$。
  2. 从 $T$ 到 $S$ 的边 $(v, u)$ ：若存在，残留网络中反向边 $(u, v)$ 的容量为 $f(v, u)$ 。但 $S$ 中的点无法到达 $T$ 中的点，故残留容量 $c_f(v, u) = 0 ⇒ f(v, u) = 0$ 。

因此，存在割 $\{S, T\}$ 使得流值等于割容量。结合上述的最大流不超过任意流，最大流最小割定理得证。

实际上最开始的充分性证明和这个也是完全一样的 qwq 。

进阶推导：算法变种

既然最小割和最大流的相似度如此知道，站在万恶的出题人视角也肯定是不会轻易放你们过去的。也就是说最小割比最大流还要凶险，会考到一些各种各样的性质或者小技巧，接下来就是 trick 专场。

首先必要的，输出最小割方案怎么办？根据上面证明最大流最小割定理的过程，我们不难发现，只要沿着残量网络的源点出发，能到达的点就是 $S$ 集合，否则为 $T$ 集合。

那么关于这一部分的代码非常的显而易见，DFS 一遍就可以了，大概是下面这样的意思：

1
2
3
4
5
6
7
void dfs(int u) {
  vis[u] = 1;
  for (int i = lnk[u]; i; i = nxt[i]) {
    int v = ter[i];
    if (!vis[v] && val[i]) dfs(v);
  }
}

然后有一种经典的问题就是二者选其一，大概描述如下：有 $n$ 个物品和两个集合 $A,B$，如果一个物品没有放入 $A$ 集合会花费 $a_i$，没有放入 $B$ 集合会花费 $b_i$；还有若干个形如 $u_i,v_i,w_i$ 的限制条件，表示如果 $u_i$ 和 $v_i$ 同时不在一个集合会花费 $w_i$，每个物品必须且只能属于一个集合，求最小的代价。

这种也是考验建模的题目。建立源汇点 $s,t$，第 $i$ 个物品从 $s$ 连容量 $a_i$ 的边、向 $t$ 连容量 $b_i$ 的边。对于每一个限制条件，在 $u,v$ 之间建立容量为 $w$ 的双向边。这时候如果源汇点不连通，说明每个物品都已经选择了自己的集合，只需求一个最小割即可。

最大权值闭合图，即给定一张有向图，每个点都有一个权值（可以为正或负或 $0$），你需要选择一个权值和最大的子图，使得子图中每个点的后继都在子图中。

做法：建立超级源点 $s$ 和超级汇点 $t$，若节点 $u$ 权值为正，则 $s$ 向 $u$ 连一条有向边，边权即为该点点权；若节点 $u$ 权值为负，则由 $u$ 向 $t$ 连一条有向边，边权即为该点点权的相反数。原图上所有边权改为 $\infty$。跑网络最大流，将所有正权值之和减去最大流，即为答案。

几个小结论来证明：

  1. 每一个符合条件的子图都对应流量网络中的一个割。因为每一个割将网络分为两部分，与 $s$ 相连的那部分满足没有边指向另一部分，于是满足上述条件。这个命题是充要的。
  2. 最小割所去除的边必须与 $s$ 和 $t$ 其中一者相连。因为否则边权是 $\infty$，不可能成为最小割。
  3. 我们所选择的那部分子图，权值和 = 所有正权值之和 - 我们未选择的正权值点的权值之和 + 我们选择的负权值点的权值之和。当我们不选择一个正权值点时，其与 $s$ 的连边会被断开；当我们选择一个负权值点时，其与 $t$ 的连边会被断开。断开的边的边权之和即为割的容量。于是上述式子转化为：权值和 = 所有正权值之和 - 割的容量。
  4. 于是得出结论，最大权值和 = 所有正权值之和 - 最小割 = 所有正权值之和 - 最大流。

注意啦，这里的割边不是传统的桥的那种割边，是指分割源点集和汇点集的那些边，可以给出一些例子证明：

（1）最小割的割边不一定是桥

例子：
考虑下图，源点 $ s $ 连接到节点 $ a $ 和 $ b $，两者均连接到汇点 $ t $，所有边容量为 1：

1
2
s --1--> a --1--> t  
s --1--> b --1--> t
  • 最小割：割断 $ s \to a $ 和 $ s \to b $（总容量为 2）。
  • 是否为桥：删除任意一条边（如 $ s \to a $），剩余边 $ s \to b \to t $ 仍连通，因此这些边不是桥。
  • 结论：最小割的边无需是桥。

（2）桥不一定是最小割的割边

例子：
在以下流网络中，边 $ a \to b $ 是桥（删除后图不连通），但容量极大：

1
2
s --1--> a --100--> b --1--> t  
s --1--> c --1--> t
  • 最小割：割断 $ s \to a $ 和 $ s \to c $，总容量为 2（而非割断高容量的桥 $ a \to b $）。
  • 结论：桥可能因容量过大而不属于最小割。

然后就是关于最小割的割边怎么算的问题了，其实也很简单：

如果需要在最小割的前提下最小化割边数量，那么先求出最小割，把没有满流的边容量改成 $\infty$，满流的边容量改成 $1$，重新跑一遍最小割就可求出最小割边数量；如果没有最小割的前提，直接把所有边的容量设成 $1$，求一遍最小割就好了。

这样直接按照最小割的定义来跑一跑就可以得到的结果。

算法其三：七星流离全不靠

  • 费用流计算之算法推导

算法推导：SSP 算法

关于费用流的话，一开始上面也就说过了，一般常见的就是最小费用最大流。这个也没啥，由于费用 $w$ 也满足斜对称性，我们也可以执行退流操作，那么就和 FF 方法里面提到的一样，找到一个单位费用最小的增广路，不断增广。反映到代码上，就是用 SPFA 替换掉 BFS 的过程，然后其他的一样就可以。

那么关于 EK 算法，我们可以拓展出这样的计算费用流代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// EK 算法拓展
struct qxx {
  int nex, t, v, c;
};

qxx e[M];
int h[N], cnt = 1;

void add_path(int f, int t, int v, int c) {
  e[++cnt] = qxx{h[f], t, v, c}, h[f] = cnt;
}

void add_flow(int f, int t, int v, int c) {
  add_path(f, t, v, c);
  add_path(t, f, 0, -c);
}

int dis[N], pre[N], incf[N];
bool vis[N];

bool spfa() {
  memset(dis, 0x3f, sizeof(dis));
  queue<int> q;
  q.push(s), dis[s] = 0, incf[s] = INF, incf[t] = 0;
  while (q.size()) {
    int u = q.front();
    q.pop();
    vis[u] = false;
    for (int i = h[u]; i; i = e[i].nex) {
      const int &v = e[i].t, &w = e[i].v, &c = e[i].c;
      if (!w || dis[v] <= dis[u] + c) continue;
      // 记录 SPFA 找到的增广路，incf 就是增广路最大的流量
      dis[v] = dis[u] + c, incf[v] = min(w, incf[u]), pre[v] = i;
      if (!vis[v]) q.push(v), vis[v] = true;
    }
  }
  // 如果流量为 0 说明行不通
  return incf[t];
}

int maxflow, mincost;

void update() {
  // 处理找到的增广路
  maxflow += incf[t];
  for (int u = t; u != s; u = e[pre[u] ^ 1].t) {
    e[pre[u]].v -= incf[t], e[pre[u] ^ 1].v += incf[t];
    mincost += incf[t] * e[pre[u]].c;
  }
}

// 调用：while(spfa())update();

EK 算法属于比较基本比较模拟的运用，Dinic 的拓展显得会略略有一点思考价值，多路增广的时候还要保证费用少，所以可以用 SPFA 处理出来的最短路数组 dis 推，再多路增广的同时保证是最短路即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
// Dinic 算法拓展
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>

constexpr int N = 5e3 + 5, M = 1e5 + 5;
constexpr int INF = 0x3f3f3f3f;
int n, m, tot = 1, lnk[N], cur[N], ter[M], nxt[M], cap[M], cost[M], dis[N], ret;
bool vis[N];

void add(int u, int v, int w, int c) {
  ter[++tot] = v, nxt[tot] = lnk[u], lnk[u] = tot, cap[tot] = w, cost[tot] = c;
}

void addedge(int u, int v, int w, int c) { add(u, v, w, c), add(v, u, 0, -c); }

bool spfa(int s, int t) {
  memset(dis, 0x3f, sizeof(dis));
  memcpy(cur, lnk, sizeof(lnk));
  std::queue<int> q;
  q.push(s), dis[s] = 0, vis[s] = true;
  while (!q.empty()) {
    int u = q.front();
    q.pop(), vis[u] = false;
    for (int i = lnk[u]; i; i = nxt[i]) {
      int v = ter[i];
      if (cap[i] && dis[v] > dis[u] + cost[i]) {
        dis[v] = dis[u] + cost[i];
        if (!vis[v]) q.push(v), vis[v] = true;
      }
    }
  }
  return dis[t] != INF;
}

int dfs(int u, int t, int flow) {
  if (u == t) return flow;
  vis[u] = true;
  int ans = 0;
  for (int &i = cur[u]; i && ans < flow; i = nxt[i]) {
    int v = ter[i];
    if (!vis[v] && cap[i] && dis[v] == dis[u] + cost[i]) {
      int x = dfs(v, t, std::min(cap[i], flow - ans));
      if (x) ret += x * cost[i], cap[i] -= x, cap[i ^ 1] += x, ans += x;
    }
  }
  vis[u] = false;
  return ans;
}

int mcmf(int s, int t) {
  int ans = 0;
  while (spfa(s, t)) {
    int x;
    while ((x = dfs(s, t, INF))) ans += x;
  }
  return ans;
}

int main() {
  int s, t;
  scanf("%d%d%d%d", &n, &m, &s, &t);
  while (m--) {
    int u, v, w, c;
    scanf("%d%d%d%d", &u, &v, &w, &c);
    addedge(u, v, w, c);
  }
  int ans = mcmf(s, t);
  printf("%d %d\n", ans, ret);
  return 0;
}

算法实战：虚心平意候枭卢

查看相关算法标签喵！

参考资料（以下排名不分先后）