浅析 Tarjan 算法

算法简介

~~由 $\tt Robert\ Tarjan$ 发明（useless。~~ 可以求强连通分量、缩点、割点、桥等，大大滴实用。

前置知识 : Dfs 树

定义：一个图按照 Dfs 的顺序建立成的生成树。
规则就是，按照 Dfs 的顺序，可以走就走，不可以走重复的点，走完为止。

在树上的边称为树边，不在树上的是非树边。

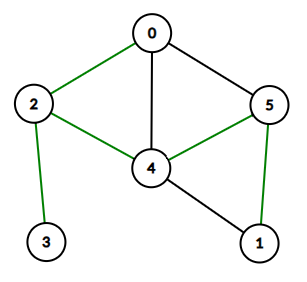
如图， $0$ 是根，绿色的是树边，黑色的是返祖边。

那么实现也很简单，为了完成这样一个功能（区分树边和返祖边）。我们就要标记一个点有没有走过，走到一个没有走过的点，这条边就是树边，走到一个走过的点，那这个就是返祖边（对于无向图）。

void Dfs(int u, int fa) {
    vis[u] = 1;
    for(int i = hd[u]; i; i = e[i].nt) {
        int v = e[i].to;
        if(!vis[v]) {
            //树边
            Dfs(v, u);
        }
        else {
            //返祖边
        }
    }
}

求割点

首先，我们来介绍割点是什么概念。所谓割点，就是当一个连通图删去一个点时，这个图就会分裂成好几块（即变得不连通）。这就是割点。

好，那么割点有什么特点呢？首先对于我们连通图的 Dfs 树，他的根节点如果有两个及以上的子树，那么这个根他就是一个割点。为什么？来看证明。

一个不是很严格的证明：

首先我们知道：对于无向图，非树边是以返祖边形式呈现的。所以，什么时候删除一个点他仍然连通呢？
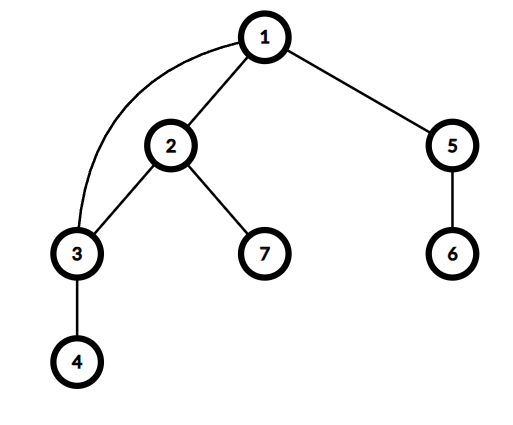
我们发现，当一个点，它的几个以儿子为根的子树如果有返祖边不可以回到自己的祖先方向（不包括自己），那么就可以分裂。举个例子：

这样，以根节点 $1$ 的儿子 $2$ 号点为根的子树中 $3$ 号点，可以连接到 $2$ 号点的父亲方向，但是，由于他的另一个儿子 $7$ 号点不可以回到 $2$ 号点的父亲方向，所以 $2$ 号点是割点。

由此可知，由于根节点压根没有父亲，所以也就都到达不了祖先方向了。

那么在说明上面的情况时，也同样说明了另外一种情况，即：当一个点的几个以儿子为根的子树中如果有点通过返祖边和树边（只能从儿子方向走）不可以回到自己的祖先方向（不包括自己），那么就可以分裂。

那么基本思路已经解释完成了，如何用代码表示出来呢？

首先对于基本的变量声明，我们使用到的，要求出一个点通过儿子边和返祖边所可以到达的最高点，我们就是用 $low[i]$ 表示一个点通过最多一个非树边所可以到达最早的点。但是，一个点的早晚我们并不可以直接求，所以我们还需要一个数组 $dfn[i]$ 表示这个点是什么时候走到的。同时标记一个点有没有访问也可以表示了，我们用第一个访问到的点标为 $1$ ，那么当一个点的 $dfn[]$ 值是 $0$ 时，代表没有走过。

现在来看代码：

void tarjan(int u){
	int tot=0;
	low[u]=dfn[u]=++cntd;
	for(int i=hd[u]; i; i=e[i].nt){
		if(!dfn[e[i].to]){
			tarjan(e[i].to, u);
			low[u]=min(low[u], low[e[i].to]);
			if(low[e[i].to]>=dfn[u]){
				tot++;
				if(u!=root||tot>1){
					vis[u]=1;
				}
			}
		}else{
			low[u]=min(low[u], dfn[e[i].to]);
		}
	}
}

求割边

顾名思义，割边就是和各店差不多，即：删除一条边使得这个图不连通，那么这条边就是割边。

那么，什么时候会有割边或者说割边的性质是什么呢？我们还是画图探究。

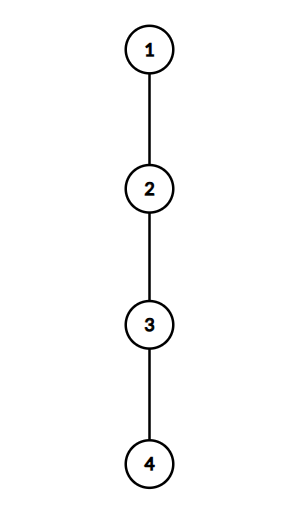
我们先使用简单的图来猜测一下：

这张图抛出来的结果十分显然。我们发现所有的都是割边，按照原来的 $low$ 值定义，那么我们得出的判定式将是：$low[q] \ge dfn[p]$ 表示边 $(p, q)$ 是割边。

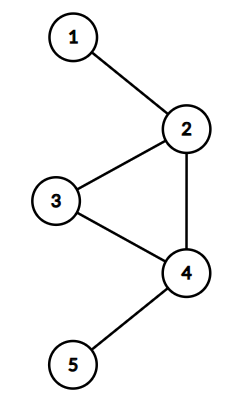
可是显而易见，这张图太随便了，完全没有任何的可靠性，所以需要造别的数据去验证。所以经过我长达 $10\tt \ min$ 的寻找，终于找到了一个可以卡掉他的数据：

我们发现跑出来的结果：除了边 $(2, 4)$ 不是割边，其他都是割边。显而易见这是不正确的。问题就出在我们让这个 $(p, q)$ 边的反向边可以走（因为这个是无向图），这样基本上都是可以达到 $low[q] \ge dfn[p]$ 的条件。所以需要禁止这个边。所以 $low[]$ 定义就变成了一个点通过最多一个非树边所可以到达最早的点（不可以走自己至父亲的反向边）。但是发现仍然不正确。经过简单的推敲发现判定式应该是 $low[q] \gt dfn[p]$ 。至此我们也就搞完了这个割边的理论判定。接下来，上代码！

void Tarjan(int u, int fa) {
    low[u] = dfn[u] = ++cnt;
    for(int i = hd[u]; i; i = e[i].nt) {
        int v = e[i].to;
        if(!dfn[v]) {
            Tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(low[v] > dfn[u]) {
                // 是割边
            }
        }
        else if(v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}