算法简介：如影流露的冷刃

递归和回溯，亲家兄弟如影随形，几乎哪里都能看到他们，所以说这里的副标题是万物根基。递归的思想，相信都不陌生，就是把所有的问题分成小块小块的去解决。而回溯，就是在递归完了之后，往回走，再接着递归。这种一步一步的枚举方式，可以很方便的穷举出所有的情况结果，这个就是递归。

像我们熟知的算法动态规划，它最初的形态也是递归，不过因为递归的特性而不利于优化，所以呢后续就有了非递归形式的动规，而各种神奇的动规优化方式也接踵而来。

算法演示：层见叠出的谜象

正如标题，层见叠出，就是递归的基本特征。对于斐波那契数列，相信大家都不陌生，我们可以用下列的函数来表示斐波那契的值：

这就可以称为递归的基本形式了。如果我们要求第 $3$ 个斐波那契数，就会根据函数的指导去算第 $1,2$ 个斐波那契数，我们会发现递归的函数会在求值的过程中，不断地反复调用自己，直到我们找到了一个临界值，斐波那契这里的话临界值是 $x\le 2$ 。

那么我们可以再找找更多的细节，注意到我在斐波那契的函数前面增加了一个 $x$ 是正整数。为什么要这样做？试想一下，如果 $x$ 是小数，是负数，是零，这个函数不就没有意义了吗。你总不能说我们要算第 -1 个斐波那契数，第 2.5 个斐波那契数罢。

其次，对于设定了临界值是 $x\le 2$ 这是为什么呢？我们发现如果不设定这样的临界值，我们照常递归，对于 $\operatorname f(2)$ 会调用 $\operatorname f(1)$ 和 $\operatorname f(0)$ 上文我们就说过这是没有意义的，对于 $\operatorname f(1)$ 也一样。

于是乎我们不难得出代码：

1
2
3
4
void Fibonacci(int x) {
    if(x <= 2) return 1;
    return Fibonacci(x - 1) + Fibonacci(x - 2);
}

例题一：倒错知能的视度

那么来到例题看看。求序列 $[1,n]$ 中取出 $k$ 个（不分顺序）的所有方案并输出。

乍一看没啥思路，但是说我们想想，组合就是每个点选或不选，那么实际上对于一个元素讨论选或者不选即可。而决定组合的两个条件，当前讨论到了哪个元素还有已经取了多少个元素，毕竟我们不能重复选也不能多选或者少选。

那么边界条件呢，他就是我们把所有答案讨论完了，那么我们必须结束，不管我们取了多少个数。其次，我们能计入答案的，就只有当取出数是 $k$ 个的时候。

当然，有些人说如果我们已经选了 $k$ 个就可以结束了之类的，确实，这是一种边界条件，毕竟之后必须全部不选才可以满足，这样就减少了大量的枚举。但是说这个并不影响我们上文说的那种枚举方式的答案，在递归中，通过特殊判断使得枚举次数减少但是答案不变的手法，叫做剪枝，剪断的剪，分支的支。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int ans[N];
void Dfs(int now, int cnt) { // now - 讨论到了哪一个元素，cnt - 选了多少个
    if(now > n) { // 所有的都考虑完
        if(cnt == k) {
            for(int i = 1; i <= cnt; i++) 
				cout << ans[i] << ' ';
            cout << "\n";
        }
        return ; // 只要所有的都讨论过，就必须结束
    }
    Dfs(now + 1, cnt); // 不选，参数意为考虑下一个，选择数量不变（也就是跳过当前）
    // 不选的情况考虑完了
    a[cnt + 1] = now; // 把选择的填入数组
    Dfs(now + 1, cnt + 1); // 选择，参数意为考虑下一个，选择数量增加（也就是选择当前）
}

// 调用：
Dfs(1, 0); // 参数意为从第一个开始考虑，目前选择了 0 个（因为一开始没有选）

算法进阶：灵犀默应的配合

那么说到递归的进阶，就是回溯。回溯是什么？要回答这个问题，我们可以先来看看递归本身。就上面的两个例子而言，递归会一直不停的不停的往下搜索，直到退出临界值，它的一大特点，就是不会回头。

比如说上面的例题，我们已经考虑过了某一个之后他不会在以后还考虑他一次，不然就有可能出现重复选择或者有顺序区别的情况，这也是我们用递归来做组合数的原因。

有人说，但是斐波那契不一样啊，比如说你要求 $\operatorname f(4)$ 他就会递归 $\operatorname f(2)$ 和 $\operatorname f(3)$ ，但是如果继续递归 $\operatorname f(3)$ 他又会重复计算了 $\operatorname f(2)$ ，这不是重复考虑了吗？显然不是。观察到，斐波那契数列的函数一直在自我调用，而且是单向的。递归所递归的子状态会完全继承父状态的所有内容。

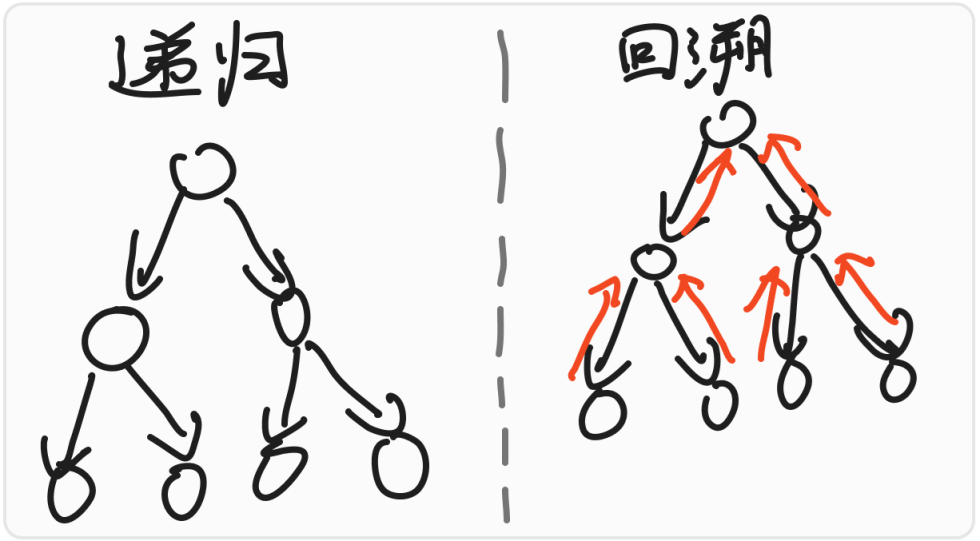
但是呢，回溯，或者说贴切的回头，他在回溯了以后，会把以前的痕迹抹除掉。我们可以用下面的模式图来区分递归还有回溯：

递归与回溯模式图

上面的模式图中，回溯的规则是有未走过的黑边就走，直到没有未走过的黑边，然后走红边回去。模拟一下就会发现递归还有回溯的区别。

那么有了回溯的性质，我们要如何去使用这个回溯呢？来一道例题。

例题二：暗昧遮目的障法

求一个 $[1,n]$ 的序列，从中取出 $k$ 个排列的方案并输出。

我们发现排列是允许有顺序的区别的，就比如说在组合中 $\{1,2\}$ 和 $\{2,1\}$ 是一样的；但是排列里这两个是不一样的。所以说我们单向的考虑肯定是不可以的。这时候就需要会回头的回溯。

那么我们同时会发现的是，我们取出 $k$ 个数排列，允许有顺序的区别，这就说明对于答案的数组，只要是我们没有选过的都可以被选择，那么我们每一次就要考虑所有的未选择数字。我们就可以用 used[i] = 1 表示这个点选了，反之就是没有选。

有了这样的基础，我们就会有下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void Dfs(int cnt) {
    if(cnt == k) {
        for(int i = 1; i <= k; i++) {
            cout << ans[i] << ' ';
        }
        cout << "\n"; 
        return ;
    }
    for(int i = 1; i <= n; i++) {
        if(!used[i]) {
            used[i] = 1;
            ans[cnt + 1] = i;
            Dfs(cnt + 1);
        }
    }
}

尝试运行一下，输入 5 5 试试水，哎，怎么输出只输出了一行 1 2 3 4 5 ？打印调试了一下，发现问题：比如我们选择了 1 之后，它的 used 不会再被改变，也就只会有一个结果 1 2 3 4 5 。于是呢，这里就提到上文说的，回溯要清除所有的痕迹，也就是说我们在处理完这个递归的结果后，回溯回来要把 used 变为 0 才可以继续，这样我们就得到了正确的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Dfs(int cnt) {
    if(cnt == k) {
        for(int i = 1; i <= k; i++) {
            cout << ans[i] << ' ';
        }
        cout << "\n"; 
        return ;
    }
    for(int i = 1; i <= n; i++) {
        if(!used[i]) {
            used[i] = 1;
            ans[cnt + 1] = i;
            Dfs(cnt + 1);
            used[i] = 0;
        }
    }
}

算法实战：示辨真意的眼睛

查看相关算法标签喵！